Storyboard

In dem Fall, dass der Fluss in einem Gas stattfindet oder in einer Situation, in der die Höhenunterschiede minimal sind, kann der Effekt des hydrostatischen Drucks vernachlässigt werden.

Ohne hydrostatischen Druck reduziert sich das Bernoulli-Gesetz auf die Summe eines Terms, der mit der kinetischen Energie und somit mit der Geschwindigkeit im Quadrat verbunden ist, und dem Druck, der an jedem Ort besteht, der konstant bleibt. Dies bedeutet, dass sich bei zunehmender Geschwindigkeit der Druck verringert und umgekehrt.

>Modell

ID:(2066, 0)

Konzept

>Top

ID:(15497, 0)

Konzept

>Top

Wenn die Energie erhalten bleibt und das Medium ohne Verformung fließt, folgt daraus, dass die Dichte zwischen zwei Punkten gleich sein muss, was die Voraussetzung für das Gesetz von Bernoulli ist.

Bei der Berechnung der Energiedichte an den Punkten 1 und 2 gilt:
• Die wissenschaftliche Energiedichte hängt von die Flüssigkeitsdichte ($\rho_w$) ab, am Punkt 1 von die Mittlere Geschwindigkeit der Flüssigkeit in Punkt 1 ($v_1$) und am Punkt 2 von die Die mittlere Geschwindigkeit der Flüssigkeit in Punkt 2 ($v_2$).
• Die potenzielle Energiedichte entspricht im Allgemeinen Punkt 1 Die Druck in Spalte 1 ($p_1$) und Punkt 2 Die Druck in Spalte 2 ($p_2$).
Wir haben die Beziehung

Diese Ausdruck kann umgeschrieben werden mit die Variación de la Presión ($\Delta p$)

mit die Durchschnittsgeschwindigkeit ($\bar{v}$)

und mit die Geschwindigkeitsunterschied zwischen Oberflächen ($\Delta v$)

schließlich ergibt sich

ID:(15503, 0)

Beschreibung

>Top

Die Geschwindigkeit eines Flugzeugs wird mit Hilfe eines sogenannten Pitotrohrs bestimmt. Dieses besteht aus zwei Öffnungen, einer vorne (Anströmkante) und einer an der Seite. An der Anströmkante ist die Geschwindigkeit null, während an der seitlichen Öffnung die Geschwindigkeit des Flugzeugs relativ zur umgebenden Luft gemessen wird. In den Öffnungen befinden sich zwei Röhren, die mit einer Flüssigkeit gefüllt sind und den Druckunterschied zwischen den beiden Punkten messen können. Mithilfe der Bernoulli-Gleichung kann so die Geschwindigkeit des Flugzeugs anhand des Druckunterschieds und der Flüssigkeitsdichte berechnet werden.

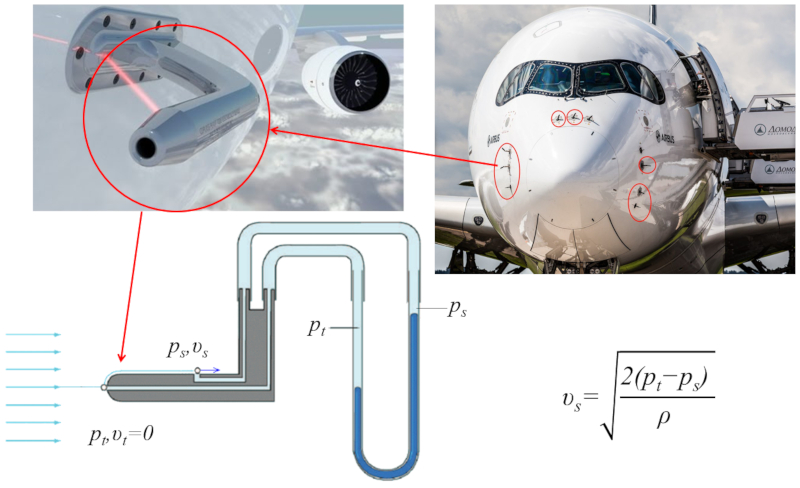
Insbesondere ist die Geschwindigkeit an der Spitze des Pitotrohrs null, was bedeutet, dass sich die Geschwindigkeitsunterschied zwischen Oberflächen ($\Delta v$) auf die Geschwindigkeit am seitlichen Öffnung ($\Delta v = v$) reduziert, während die Durchschnittsgeschwindigkeit ($\bar{v}$) der Hälfte der Geschwindigkeit entspricht ($\bar{v}=v/2$). Da die Geschwindigkeit der Fluggeschwindigkeit entspricht, kann sie durch Messung des Drucks mit der Gleichung bestimmt werden:

$v=\sqrt{\displaystyle\frac{2 \Delta p}{\rho}}$

Es ist zu beachten, dass diese Gleichung die Dichte erfordert, die mit der Flughöhe variiert.

ID:(11095, 0)

Beschreibung

>Top

Wenn ein Auto auf der Straße überholt wird, entsteht eine Situation, in der zwischen den beiden Fahrzeugen ein Luftstrom mit höherer Geschwindigkeit erzeugt wird, was zu einem niedrigeren Druck in diesem Bereich führt. Folglich führt der Druck an den äußeren Seiten der Autos dazu, dass sie sich gegenseitig anziehen.

Wenn Fahrzeuge sich kreuzen, nimmt die relative Geschwindigkeit zwischen ihnen ab und nähert sich der Ruhe, was einen höheren Druck zwischen ihnen erzeugt und sie dazu bringt, sich voneinander zu entfernen.

Das gleiche Phänomen tritt auf, wenn sich zwei Boote kreuzen. Wenn das Überqueren in einem engen Kanal stattfindet, müssen beide Steuerleute ihre Schiffe auf die gegenüberliegende Seite steuern, um zu verhindern, dass die abstoßende Kraft eine Kollision mit dem Rand des Kanals verursacht.

Um zu erklären, warum dies passiert, können wir die Gleichung die Variación de la Presión ($\Delta p$) mit die Durchschnittsgeschwindigkeit ($\bar{v}$) und die Geschwindigkeitsunterschied zwischen Oberflächen ($\Delta v$) mit die Dichte ($\rho$) anwenden:

Daher ist zu erkennen, dass bei einem Geschwindigkeitsgradienten dieser umgekehrt proportional zum Druckgradienten ist. Wenn einer steigt, fällt der andere, was erklärt, warum überholende Autos eine höhere Geschwindigkeit zwischen ihnen aufweisen, was zu einer Verringerung des Drucks zwischen ihnen führt und zu gegenseitigem Ansaugen führt. Im Gegensatz dazu ist bei einem Kreuzen die Geschwindigkeit zwischen ihnen etwa Null, was einen Druckgradienten erzeugt, der sie auseinanderdrückt.

ID:(11094, 0)

Konzept

>Top

Ausgewählter Parameter

Berechnungen

ID:(15498, 0)

Gleichung

>Top, >Modell

Da ein Fluid oder Gas ein Kontinuum ist, kann das Konzept der Energie nicht mehr mit einer spezifischen Masse verbunden werden. Es ist jedoch möglich, die Energie in einem Volumen des Kontinuums zu betrachten und durch Division durch das Volumen selbst erhalten wir die Energiedichte ($e$). Daher haben wir mit die Dichte ($\rho$), die Mittlere Geschwindigkeit der Flüssigkeit ($v$) und die Druck der Wassersäule ($p_t$):

$ e =\displaystyle\frac{1}{2} \rho v ^2+ p $

Bedingungen

Variablen

$\rho$

Dichte

$kg/m^3$

$p$

Druck der Wassersäule

$Pa$

$e$

Energiedichte

$J/m^3$

$v$

Mittlere Geschwindigkeit der Flüssigkeit

$m/s$

Beziehung

Entwicklung

Eine weitere nützliche Gleichung ist diejenige, die der Energieerhaltung entspricht und in Fällen angewendet wird, in denen die Viskosität vernachlässigt werden kann, da sie einen Prozess darstellt, bei dem Energie verloren geht. Wenn wir die klassische Energiegleichung $E$ betrachten, die die kinetische Energie, die potenzielle Gravitationsenergie und eine äußere Kraft, die die Flüssigkeit über eine Strecke $\Delta z$ verschiebt, berücksichtigt, kann sie wie folgt ausgedrückt werden:

$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$

Wenn wir die Energie innerhalb eines Volumens $\Delta x\Delta y\Delta z$ betrachten, können wir die Masse ersetzen durch:

$m=\rho \Delta x\Delta y\Delta z$

Und da der Druck gegeben ist durch:

$F=p \Delta S =p \Delta y\Delta z$

erhalten wir die Gleichung für die Energiedichte:

$ e =\displaystyle\frac{1}{2} \rho v ^2+ p $

was der Bernoulli-Gleichung entspricht.

In Abwesenheit von Viskosität impliziert die Erhaltung der Energie, dass die Energiedichte ($e$) an jedem Punkt des Fluids konstant ist. Daher reicht es aus, die Geschwindigkeit und/oder den Druck an jeder Stelle des Fluids zu kennen, um eine Beziehung zwischen Geschwindigkeit und Druck an jedem Punkt des Fluids herzustellen.

ID:(15496, 0)

Gleichung

>Top, >Modell

Wenn die Energie innerhalb der strömenden Volumina erhalten bleibt, müssen die Energiedichte in 1 ($e_1$) und die Energiedichte in 2 ($e_2$) gleich sein:

$ e_1 = e_2 $

Bedingungen

Variablen

$e_1$

Energiedichte in 1

$J/m^3$

$e_2$

Energiedichte in 2

$J/m^3$

Beziehung

Dies ist nur möglich, wenn die Viskosität vernachlässigbar ist, da sie mit der Energieverteilung verbunden ist und keine Wirbel vorhanden sind, die selbst aufgrund unterschiedlicher tangentialer Geschwindigkeiten entlang des Wirbels einen Energieunterschied aufweisen.

ID:(15499, 0)

Gleichung

>Top, >Modell

Da ein Fluid oder Gas ein Kontinuum ist, kann das Konzept der Energie nicht mehr mit einer spezifischen Masse verbunden werden. Es ist jedoch möglich, die Energie in einem Volumen des Kontinuums zu betrachten und durch Division durch das Volumen selbst erhalten wir die Energiedichte ($e$). Daher haben wir mit die Dichte ($\rho$), die Mittlere Geschwindigkeit der Flüssigkeit ($v$) und die Druck der Wassersäule ($p_t$):

$ e_1 =\displaystyle\frac{1}{2} \rho v_1 ^2+ p_1 $

$ e =\displaystyle\frac{1}{2} \rho v ^2+ p $

Bedingungen

Variablen

$\rho$

Dichte

$kg/m^3$

$p$

$p_1$

Druck in Spalte 1

$Pa$

$e$

$e_1$

Energiedichte in 1

$J/m^3$

$v$

$v_1$

Mittlere Geschwindigkeit der Flüssigkeit in Punkt 1

$m/s$

Beziehung

Entwicklung

Eine weitere nützliche Gleichung ist diejenige, die der Energieerhaltung entspricht und in Fällen angewendet wird, in denen die Viskosität vernachlässigt werden kann, da sie einen Prozess darstellt, bei dem Energie verloren geht. Wenn wir die klassische Energiegleichung $E$ betrachten, die die kinetische Energie, die potenzielle Gravitationsenergie und eine äußere Kraft, die die Flüssigkeit über eine Strecke $\Delta z$ verschiebt, berücksichtigt, kann sie wie folgt ausgedrückt werden:

$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$

Wenn wir die Energie innerhalb eines Volumens $\Delta x\Delta y\Delta z$ betrachten, können wir die Masse ersetzen durch:

$m=\rho \Delta x\Delta y\Delta z$

Und da der Druck gegeben ist durch:

$F=p \Delta S =p \Delta y\Delta z$

erhalten wir die Gleichung für die Energiedichte:

$ e =\displaystyle\frac{1}{2} \rho v ^2+ p $

was der Bernoulli-Gleichung entspricht.

In Abwesenheit von Viskosität impliziert die Erhaltung der Energie, dass die Energiedichte ($e$) an jedem Punkt des Fluids konstant ist. Daher reicht es aus, die Geschwindigkeit und/oder den Druck an jeder Stelle des Fluids zu kennen, um eine Beziehung zwischen Geschwindigkeit und Druck an jedem Punkt des Fluids herzustellen.

ID:(15496, 1)

Gleichung

>Top, >Modell

Da ein Fluid oder Gas ein Kontinuum ist, kann das Konzept der Energie nicht mehr mit einer spezifischen Masse verbunden werden. Es ist jedoch möglich, die Energie in einem Volumen des Kontinuums zu betrachten und durch Division durch das Volumen selbst erhalten wir die Energiedichte ($e$). Daher haben wir mit die Dichte ($\rho$), die Mittlere Geschwindigkeit der Flüssigkeit ($v$) und die Druck der Wassersäule ($p_t$):

$ e_2 =\displaystyle\frac{1}{2} \rho v_2 ^2+ p_2 $

$ e =\displaystyle\frac{1}{2} \rho v ^2+ p $

Bedingungen

Variablen

$\rho$

Dichte

$kg/m^3$

$p$

$p_2$

Druck in Spalte 2

$Pa$

$e$

$e_2$

Energiedichte in 2

$J/m^3$

$v$

$v_2$

Die mittlere Geschwindigkeit der Flüssigkeit in Punkt 2

$m/s$

Beziehung

Entwicklung

Eine weitere nützliche Gleichung ist diejenige, die der Energieerhaltung entspricht und in Fällen angewendet wird, in denen die Viskosität vernachlässigt werden kann, da sie einen Prozess darstellt, bei dem Energie verloren geht. Wenn wir die klassische Energiegleichung $E$ betrachten, die die kinetische Energie, die potenzielle Gravitationsenergie und eine äußere Kraft, die die Flüssigkeit über eine Strecke $\Delta z$ verschiebt, berücksichtigt, kann sie wie folgt ausgedrückt werden:

$E=\displaystyle\frac{m}{2}v^2+mgh+F\Delta x$

Wenn wir die Energie innerhalb eines Volumens $\Delta x\Delta y\Delta z$ betrachten, können wir die Masse ersetzen durch:

$m=\rho \Delta x\Delta y\Delta z$

Und da der Druck gegeben ist durch:

$F=p \Delta S =p \Delta y\Delta z$

erhalten wir die Gleichung für die Energiedichte:

$ e =\displaystyle\frac{1}{2} \rho v ^2+ p $

was der Bernoulli-Gleichung entspricht.

In Abwesenheit von Viskosität impliziert die Erhaltung der Energie, dass die Energiedichte ($e$) an jedem Punkt des Fluids konstant ist. Daher reicht es aus, die Geschwindigkeit und/oder den Druck an jeder Stelle des Fluids zu kennen, um eine Beziehung zwischen Geschwindigkeit und Druck an jedem Punkt des Fluids herzustellen.

ID:(15496, 2)

Gleichung

>Top, >Modell

Im Fall des Bernoulli-Gesetzes [1] gilt für den Fall, dass kein hydrostatischer Druck vorhanden ist, die Dichte ($\rho$), die Druck in Spalte 1 ($p_1$), die Druck in Spalte 2 ($p_2$), < var>5415 und die Die mittlere Geschwindigkeit der Flüssigkeit in Punkt 2 ($v_2$):

$\displaystyle\frac{1}{2} \rho v_1 ^2 + p_1 =\displaystyle\frac{1}{2} \rho v_2 ^2 + p_2 $

Bedingungen

Variablen

$\rho$

Dichte

$kg/m^3$

$v_2$

Die mittlere Geschwindigkeit der Flüssigkeit in Punkt 2

$m/s$

$p_1$

Druck in Spalte 1

$Pa$

$p_2$

Druck in Spalte 2

$Pa$

$v_1$

Mittlere Geschwindigkeit der Flüssigkeit in Punkt 1

$m/s$

Beziehung

La ecuación de Bernoulli asume la conservación de la densidad de energía, lo que implica la ausencia de viscosidad y turbulencia, por lo que su aplicación en este caso es limitada.

La ecuación de Bernoulli puede servir como base para modelar el proceso, pero necesariamente debe ser complementada con un modelo que considere la posibilidad de incluir los efectos de la turbulencia.

[1] "Hydrodynamica" (Hidrodinamica), Daniel Bernoulli, Typis Joh. Henr. Deckeri (1738)

ID:(15495, 0)

Gleichung

>Top, >Modell

Wenn zwei Flüssigkeitssäulen mit die Druck in Spalte 1 ($p_1$) und die Druck in Spalte 2 ($p_2$) verbunden werden, entsteht eine die Druckunterschied ($\Delta p$), die nach folgender Formel berechnet wird:

$ \Delta p = p_2 - p_1 $

Bedingungen

Variablen

$p_1$

Druck in Spalte 1

$Pa$

$p_2$

Druck in Spalte 2

$Pa$

$\Delta p$

Variación de la Presión

$Pa$

Beziehung

die Druckunterschied ($\Delta p$) repräsentiert den Druckunterschied, der dazu führt, dass die Flüssigkeit von der höheren Säule zur niedrigeren fließt.

ID:(4252, 0)

Gleichung

>Top, >Modell

Die Durchschnittsgeschwindigkeit ($\bar{v}$) ist mit die Mittlere Geschwindigkeit der Flüssigkeit in Punkt 1 ($v_1$) und die Die mittlere Geschwindigkeit der Flüssigkeit in Punkt 2 ($v_2$) ist

$ \bar{v} = \displaystyle\frac{ v_1 + v_2 }{2}$

Bedingungen

Variablen

$v_2$

Die mittlere Geschwindigkeit der Flüssigkeit in Punkt 2

$m/s$

$\bar{v}$

Durchschnittsgeschwindigkeit

$m/s$

$v_1$

Mittlere Geschwindigkeit der Flüssigkeit in Punkt 1

$m/s$

Beziehung

ID:(15501, 0)

Gleichung

>Top, >Modell

Die Geschwindigkeitsunterschied zwischen Oberflächen ($\Delta v$) ist mit die Mittlere Geschwindigkeit der Flüssigkeit in Punkt 1 ($v_1$) und die Die mittlere Geschwindigkeit der Flüssigkeit in Punkt 2 ($v_2$) ist

$ \Delta v = v_2 - v_1 $

Bedingungen

Variablen

$v_2$

Die mittlere Geschwindigkeit der Flüssigkeit in Punkt 2

$m/s$

$\Delta v$

Geschwindigkeitsunterschied zwischen Oberflächen

$m/s$

$v_1$

Mittlere Geschwindigkeit der Flüssigkeit in Punkt 1

$m/s$

Beziehung

ID:(15502, 0)

Gleichung

>Top, >Modell

Die Variación de la Presión ($\Delta p$) kann aus die Durchschnittsgeschwindigkeit ($\bar{v}$) und die Geschwindigkeitsunterschied zwischen Oberflächen ($\Delta v$) mit die Dichte ($\rho$) berechnet werden

$ \Delta p = - \rho \bar{v} \Delta v $

Bedingungen

Variablen

$\rho$

Dichte

$kg/m^3$

$\bar{v}$

Durchschnittsgeschwindigkeit

$m/s$

$\Delta v$

Geschwindigkeitsunterschied zwischen Oberflächen

$m/s$

$\Delta p$

Variación de la Presión

$Pa$

Beziehung

Entwicklung

Für den Fall, dass kein hystrostatischer Druck vorhanden ist, gilt das Bernoulli-Gesetz für die Flüssigkeitsdichte ($\rho_w$), die Druck in Spalte 1 ($p_1$), die Druck in Spalte 2 ($p_2$), die Mittlere Geschwindigkeit der Flüssigkeit in Punkt 1 ($v_1$) und < var>5416



kann mit umgeschrieben werden die Variación de la Presión ($\Delta p$)



und das im Hinterkopf behalten

$v_2^2 - v_1^2 = \displaystyle\frac{1}{2}(v_2-v_1)(v_1+v_2)$

mit



Und



du musst

Dies ermöglicht es uns, den Einfluss der Durchschnittsgeschwindigkeit eines Körpers und des Unterschieds zwischen seinen Oberflächen zu sehen, wie er bei einem Flugzeug oder einem Vogelflügel beobachtet wird.

ID:(4835, 0)