Utilisateur:
Champ électrique
Storyboard 
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
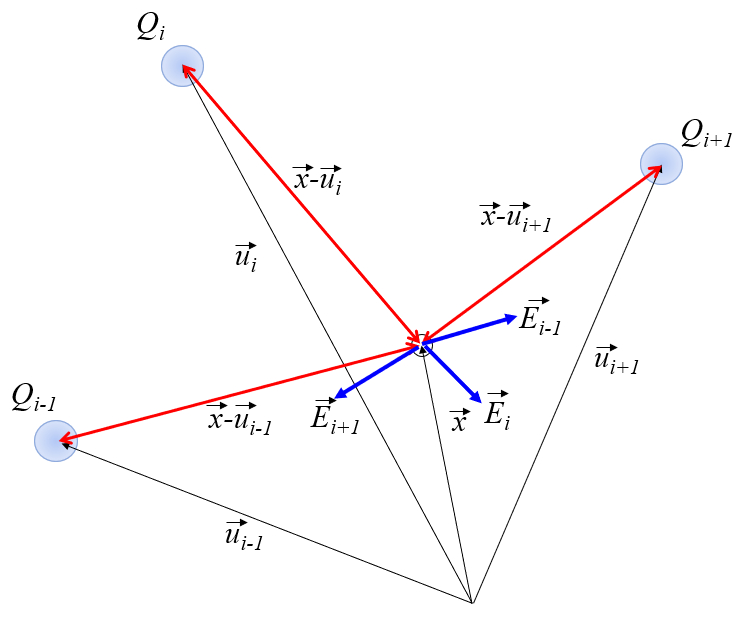
A force ($\vec{F}$) sur a charge d'essai ($q$) A position ($\vec{r}$) d pendra de le nombre de charges ($N$), index par $i$ et repr sent par a charge des ions i ($Q_i$) situ a position d'une charge i ($\vec{u}_i$). Avec les param tres a constante diélectrique ($\epsilon$) et a constante de champ électrique ($\epsilon_0$), cela peut s' crire comme suit :
Avec la d finition de le champ électrique ($\vec{E}$) donn e par
il s'ensuit que le champ lectrique d'une distribution de charges est
La magnitude de a force à masse constante ($F$) g n r e entre deux charges, repr sent es par a charge d'essai ($q$) et a charge ($Q$), qui se trouvent une distance de a distance ($r$), se calcule en utilisant a constante de champ électrique ($\epsilon_0$) et a constante diélectrique ($\epsilon$) de la mani re suivante :
En utilisant la d finition du champ lectrique comme
on obtient
Exemples
Pour mesurer la force de Coulomb, il est n cessaire d'introduire une charge de test dans le syst me. Si cette charge de test est a charge d'essai ($q$), on peut estimer la force par unit de charge que les charges du syst me exercent sur la charge de test. La magnitude de la force a force ($\vec{F}$) par unit de charge a charge d'essai ($q$) est appel e champ lectrique le champ électrique ($\vec{E}$) et est mesur e en Newtons (N) par Coulomb (C). Le champ lectrique est mesur en supposant que la charge de test ne perturbe pas significativement le syst me ; en d'autres termes, elle est suppos e tre tr s petite. La d finition du champ peut tre crite comme suit :
Dans le cas o la g om trie permet de travailler de mani re unidimensionnelle, a force à masse constante ($F$) par a charge d'essai ($q$) peut tre d fini en introduisant le champ électrique ($E$), ce qui s'exprime comme suit :
La magnitude de a force à masse constante ($F$) g n r e entre deux charges, repr sent es par a charge d'essai ($q$) et a charge ($Q$), qui se trouvent une distance de a distance ($r$), se calcule en utilisant a constante de champ électrique ($\epsilon_0$) et a constante diélectrique ($\epsilon$) de la mani re suivante :
En utilisant la d finition du champ lectrique comme
on obtient
A force ($\vec{F}$) sur a charge d'essai ($q$) A position ($\vec{r}$) d pendra de le nombre de charges ($N$), index par $i$ et repr sent par a charge des ions i ($Q_i$) situ a position d'une charge i ($\vec{u}_i$). Avec les param tres a constante diélectrique ($\epsilon$) et a constante de champ électrique ($\epsilon_0$), cela peut s' crire comme suit :
Avec la d finition de le champ électrique ($\vec{E}$) donn e par
il s'ensuit que le champ lectrique d'une distribution de charges est
L' quation peut tre repr sent e graphiquement de la mani re suivante :
A force ($\vec{F}$) pour a charge d'essai ($q$) est d fini comme le champ électrique ($\vec{E}$), qui s'exprime comme suitxa0:
A force à masse constante ($F$) pour a charge d'essai ($q$) est d fini comme le champ électrique ($E$), qui s'exprime comme suitxa0:
Une fois que le champ électrique ($E$) est connu, a force à masse constante ($F$), qui agit sur a charge ($q$), peut tre calcul en utilisant :
Une fois que le champ électrique ($\vec{E}$) est connu, a force ($\vec{F}$), qui agit sur a charge ($q$), peut tre calcul en utilisantxa0:
La magnitude de le champ électrique ($E$) g n r e par a charge ($Q$), qui se trouvent une distance de a distance ($r$), se calcule en utilisant a constante de champ électrique ($\epsilon_0$) et a constante diélectrique ($\epsilon$) de la mani re suivante :
Le champ électrique ($\vec{E}$) A position ($\vec{r}$) d pendra de le nombre de charges ($N$), index par $i$ et repr sent par a charge des ions i ($Q_i$) situ a position d'une charge i ($\vec{u}_i$). Avec les param tres a constante diélectrique ($\epsilon$) et a constante de champ électrique ($\epsilon_0$), cela peut tre crit comme suit :
ID:(814, 0)
