Usuario:
Mecanismo de la Ruptura
Storyboard 
Cuando ocurre una ruptura, se caracteriza por una zona que ya no puede soportar carga y un borde que se caracteriza por una tensión que aumenta inversamente al radio de la punta de la fractura. Esto implica que la sección se reduce, lo que conlleva a que la sección restante deba soportar una carga mayor, exacerbando la situación en la punta de la fractura y facilitando su propagación. De esta manera, se produce una situación catastrófica en la que cada incremento en la fractura aumenta la carga a soportar, lo que a su vez provoca un aumento en la fractura.
ID:(2067, 0)
Mecánica de ruptura
Descripción
La mecánica de la ruptura consiste en que previo a la fractura el cuerpo tiene energía cinética y/o potencial. Por una acción descuidada el cuerpo apoya una parte menor del cuerpo (ej. solo la muñeca) y se expone a que toda la energía tenga que ser absorbida por dicha parte. Si la energía que debe de absorber la parte sobrepasa la energía crítica de alguno de los mecanismos de ruptura, sera dicho mecanismo el que finalmente se presentará. Si la energía no es suficiente para alcanzar cualquiera de las energías críticas no ocurrirá la ruptura.
ID:(742, 0)
Tensiones en torno a la punta de un quiebre
Imagen
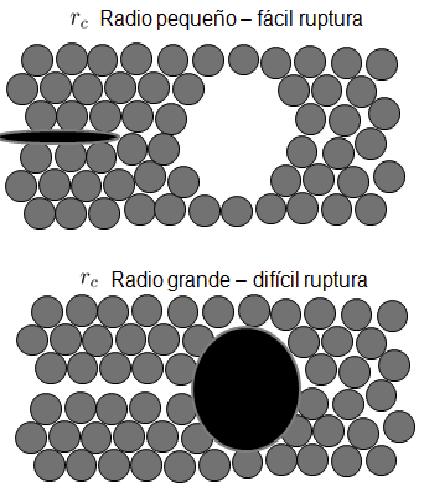
La propagación de la fractura se produce porque la punta de ésta tiene un radio extremadamente pequeño, lo que implica una tensión muy alta, ya que ésta es proporcional al inverso de la raíz cuadrada del radio.
El avance de la fractura puede detenerse si en algún momento el radio aumenta, reduciendo la tensión en la punta. Esto se logra, por ejemplo, mediante la porosidad del material o la inserción de inhomogeneidades que actúan como un punto de concentración de tensión.
None
ID:(1691, 0)
Modelo
Top
Cálculos
Variables
Parámetros
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar Ecuación
$ K_I =\sqrt{\displaystyle\frac{ F E }{ l }}$
K_I =sqrt( F * E / l )
$ \sigma_y =\displaystyle\frac{ K_i }{\sqrt{2 \pi r_p }}$
s_y = K_i /sqrt(2* pi * r_p )
$\sigma_x(r,\theta)=\displaystyle\frac{K_i}{\sqrt{2pi r}}\cos\displaystyle\frac{\theta}{2}\left(1-\sin\displaystyle\frac{\theta}{2}\sin\displaystyle\frac{3\theta}{2} \right)$
s_x(r,theta)=(K_i/sqrt(2 pi r))cos(theta/2)(1-sin(theta/2)sin(3theta/2))
$ \sigma_y =\displaystyle\frac{ K_i }{\sqrt{2 \pi r }}\cos\displaystyle\frac{\theta}{2}\left(1-\sin\displaystyle\frac{ \theta }{2}\sin\displaystyle\frac{3 \theta }{2}\right)$
s_y(r,theta)=(K_i/sqrt{2 pi r))cos(theta/2)(1 sin(theta/2)sin(3theta/2))
ID:(15578, 0)
Factor Intensidad
Ecuación
The breaking stress is proportional to the el factor de intensidad ($K_I$), which is proportional to the square root of la fuerza ($F$), el módulo de Elasticidad ($E$), and el largo de quiebre ($l$):
| $ K_I =\sqrt{\displaystyle\frac{ F E }{ l }}$ |
ID:(3785, 0)
Tensión en la punta del quiebre
Ecuación
La tensión en la punta del quiebre es proporcional al factor de intensidad
| $ \sigma_y =\displaystyle\frac{ K_i }{\sqrt{2 \pi r_p }}$ |
ID:(3786, 0)
Tensión paralelo a la ruptura
Ecuación
La tensión en la dirección paralela
| $\sigma_x(r,\theta)=\displaystyle\frac{K_i}{\sqrt{2pi r}}\cos\displaystyle\frac{\theta}{2}\left(1-\sin\displaystyle\frac{\theta}{2}\sin\displaystyle\frac{3\theta}{2}
\right)$ |
ID:(3788, 0)
Tensión perpendicular a la ruptura
Ecuación
La tensión en la dirección perpendicular
| $ \sigma_y =\displaystyle\frac{ K_i }{\sqrt{2 \pi r }}\cos\displaystyle\frac{\theta}{2}\left(1-\sin\displaystyle\frac{ \theta }{2}\sin\displaystyle\frac{3 \theta }{2}\right)$ |
ID:(3787, 0)