Coeficiente de Difusión de Stokes–Einstein
Ecuación 
El coeficiente de difusión según el modelo de Stokes Einstein es
ID:(8380, 0)
Parámetros de la Glucosa
Descripción 
La glucosa tiene la formula C_6H_{12}O_6 tiene los parametros
Parametros | Valor | Unidad
-----------------|---------|----------
Masa molar | 180.16 | g/mol
Densidad | 1.54 | g/cm3
Volumen molar | 116.98 | cm3/mol
Radio medio | 3.6E-10 | m
En la sange los parametros son
Parametros | Valor | Unidad
-----------------|---------|----------
Nivel en sangre | 100 | mg/dl
- | 5.5 | mmol/l
- | 3.41E+6 |1/um3
Difusión en agua | 706.41 | um2/s
Difusión en sangre | 523.92 | um2/s
ID:(8393, 0)
Radio medio de Glucosa
Descripción 
La glucosa tiene la formula C_6H_{12}O_6 con una masa molar de
M_m = 180.16 g/mol
y una densidad de
\rho = 1.54 g/cm^3.
Por ello se tiene que cada molécula en un mol de glucosa ocuparía un volumen de
V_m = \displaystyle\frac{M_m}{\rho}=\displaystyle\frac{180.16 g/mol}{1.54 g/cm^3}=116.98 cm^3/mol
y el volumen de una molécula es
v=\displaystyle\frac{V_m}{N_A}=1.94\times 10^{-22}cm^3
donde N_A es el número de Avogadro.
Si se asume una forma esférica el radio a
v=\displaystyle\frac{4\pi}{3}a^3
este último sería del orden de
a = \left(\displaystyle\frac{3}{4\pi}v\right)^{1/3}=3.6\times 10^{-10}m.
ID:(8851, 0)
Constante de Difusión
Descripción 
Si se estima la constante de difusión de la molécula de glucosa en agua con la ecuación de Stokes-Einstein a temperatura de
T=36C\sim 309K
y se asume una viscosidad de
Liquido | Viscosidad (mPa s)
-----------|-------------------
Agua | 0.89
Plasma | 1.2
se tiene que con
| D=\displaystyle\frac{kT}{6\pi\eta r} |
esta será del orden de
Liquido | Constante Difusión (um2/s)
-----------|-------------------
Agua | 706.41
Plasma | 523.92
ID:(8850, 0)
Flujos de Glucosa
Descripción 
La concentración de glucosa en la sangre es de
c=\displaystyle\frac{\rho}{M_m}=\displaystyle\frac{1.54g/cm^3}{180.16g/mol}=8.527,mmol/l=5.133\times 10^4,1/\mu m^3.
Si el sistema de modela con cubitos del ancho de la membrana basal/cavidad astrocito-neurona d de 0.02um y si el gradiente fuera dado por la concentración c (máximo gradiente que se pudiera dar) se tiene que por una sección de este cubo (d^2\sim 4\times 10^{-4}\mu m) el flujo sería de
J\sim D,d,c\sim 7.25\times 10^51/s
moléculas de glucosa.
ID:(8852, 0)
Estructura general del Modelo
Imagen 
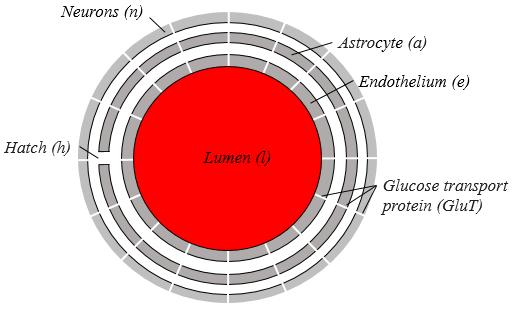
El modelo consta de tres cilindros que serian el endotelio, la membrana basal y el sistema externo (neurona y/o astrocitos). Entre las tres membranas hay dos espacios en que pueden difundir los iones. Las membranas mismas presentan bombas de glucosa (GluT) y existe una apertura a través de la membrana basal (el hatch):
ID:(8450, 0)
Variables del Modelo
Imagen 
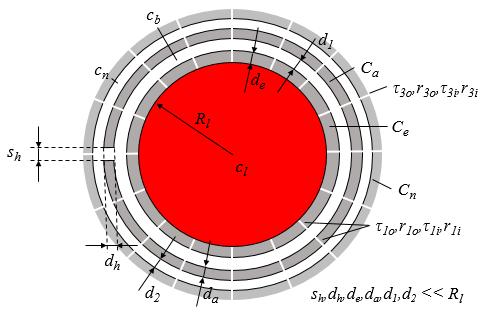
La parte geométrica es descrita por:
Variable | Simbolo | Valor
------------|:------:|-------
Radio del lumen | R_l | 10 um
Grosor del endotelio | d_e | 0.2 um
Grosor del astrocito | d_a | 0.2 um
Ancho membrana basal | d_1 | 0.02 um
Ancho cavidad entre astrocito y neurona | d_2 | 0.02 um
Largo de la apertura (al no ser necesariamente recto d_h puede ser mayor que d_a) | d_h | 0.7 um
Ancho de apertura | s_h | 0.02 um
mientras que las bombas de glucosa (GluT) se describen por
- C número por área,
- r_o, r_i radio dirección out/in en que logran capturar y
- \tau_o, \tau_i tiempo dirección out/in de reactivación
con los subindices de la membrana que que están operando (e-endotelio C_e, a-astrocito C_a y n-neurona C_n). Los GluT se diferencian si son del tipo 1 o 3 y les definimos radio de acción y tiempo tanto en el sentido hacia afuera (o-out) como adentro (i-in) (\tau_{1o}, r_{1o}, \tau_{1i}, r_{1i}, \tau_{3o}, r_{3o}, \tau_{3i}, r_{3i}). En caso que se desee modelar los en forma simétrica basta tomar tiempos y radios iguales (\tau_{1o}=\tau_{1i}, r_{1o}=r_{1i}, \tau_{3o}=\tau_{3i}, r_{3o}=r_{3i}).
En general se puede asumir una concentración de glucosa pareja en el lumen homogénea c_l dado que con el tamaño que presenta y el de los glóbulos rojos se puede esperar turbulencias que homogeneizan.
Ademas se tienen las concentraciones
- c_a entre la membrana basal y
- c_n entre el astrocito y la neurona
- c_e exterior, sink neurona
La primera es una función del radio r mientras que las segundas de un parámetro s que recorre el perímetro y tiene su origen en la apertura (hatch):
ID:(8451, 0)
Modelo de la Transportador de Glucosa
Imagen 
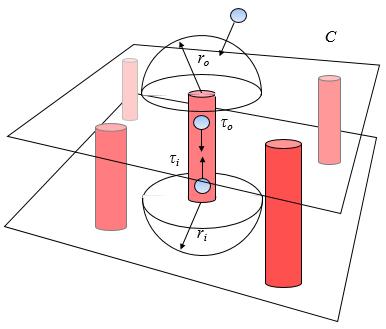
Se modela la bomba de glucosa como un sistema que cada vez que esta activa y una molécula de glucosa llega hasta una distancia r la captura y transporta.
Se supone ademas que requiere de un tiempo \tau para realizar el transporte y/o cualquier otro proceso necesario para poder volver a transportar. Este mecanismo implica que la bomba presenta un mecanismo de saturación pues ante la situación que siempre exista una molécula de glucosa a su alcance, solo podrá generar un flujo de una molécula por cada tiempo \tau (o sea 1/\tau).
Adicionalmente se supone que las bombas están presentes en una concentración por área igual a C.
El digamma a continuación busca gratificar el área de acción r, el tiempo de re activación \tau y la concentración C:
ID:(8452, 0)
Flujo Saturado
Ecuación 
Si los transportadores actúa en una membrana de radio R que se extiende por un largo \Delta z y si su concentración superficial es C existiran
2\pi R \Delta z C
de estos.
Como cada una traslada en el tiempo \tau una molécula el flujo máximo sería
| J_s=\displaystyle\frac{2\pi R \Delta z C}{\tau} |
Datos sobre concentración de GluT's: J Cereh Blood Flow Metab, Vol. 18, No.1, 1998.
ID:(8545, 0)
Flujo Saturado por Largo
Ecuación 
Como el capilar se representa como un cilindro, tiene sentido expresar una serie de magnitudes por largo. Es por ello que se puede definir un flujo saturado por largo dividiendo el flujo J por el largo \Delta z:
| j_s=\displaystyle\frac{J_s}{\Delta z} |
ID:(8546, 0)
Flujo Saturado por Largo en el Modelo
Ecuación 
Si se toma el flujo saturado
| J_s=\displaystyle\frac{2\pi R \Delta z C}{\tau} |
y se divide por \Delta z se obtiene el flujo saturado por largo
| j_s=\displaystyle\frac{J_s}{\Delta z} |
que en este caso sería
| j_s=\displaystyle\frac{2\pi R C}{\tau} |
Las concentraciones C de los GluT pueden ser estimados, el radio R es del orden de 10 um y si se asume que se traslocan 1000 moleculas por segundo los tiempos son del orden de 1 ms y con ello los flujos
Membranes | Concentration (1/um^2) | R (um) | \tau (ms) | j_s (1/um s)
-----------------|:-----------------------------------:|:---:|:--:|:---:
Endothelial | 4.4 | 10.00 | 1 | 2.76E+5
Atrocyte/Basal laminar | 1.2 | 10.22 | 1 | 7.70E+4
Abluminal/Neuron | 0.9 | 10.44 | 1 | 5.90E+4
ID:(8454, 0)
Modelo GluT (radial)
Ecuación 
El flujo por un transportador desde el lado interior al exterior sobre un largo \Delta z es
j_{si}\displaystyle\frac{c_i}{c_{si}}\Delta z
donde j_{si} es el flujo saturado por un transportador desde el interior, c_{si} la concentración de saturación desde el interior y c_i la concentración del interior.
El flujo por un transportador desde el lado exterior al interior sobre un largo \Delta z es
j_{so}\displaystyle\frac{c_o}{c_{so}}\Delta z
donde j_{so} es el flujo saturado por un transportador desde el exterior, c_{so} la concentración de saturación desde el exterior y c_o la concentración del exterior.
Por ello el flujo total por largo \Delta z
| J=\left(j_{si}\displaystyle\frac{c_i}{c_{si}}-j_{so}\displaystyle\frac{c_o}{c_{so}}\right)\Delta z |
ID:(8472, 0)
Concentración Crítica
Ecuación 
La bomba de glucosa simplemente transporta moléculas de glucosa en la medida de que estén en el volumen en que ésta las puede capturar. Dicha zona se modela como una esfera de radio r. Si la concentración es c el número de partículas en dicha zona serán
\displaystyle\frac{2\pi}{3}r^3 c
En el caso de saturación siempre existe una molécula en la zona de captura por lo que la expresión anterior es 1 y con ello la concentración crítica
| c_s=\displaystyle\frac{3}{2\pi}\displaystyle\frac{1}{r^3} |
Para valores de K_m igual a 3-7 mM (GluT1) y 1.4 mM (GluT3) respectivamente y teniendo en cuenta de que K_m es el 50% de la concentración de saturación(c_s=2K_m), se obtiene con esta ecuación que:
Proteina | K_m | r | c_s (1/um3) | c_s (mmol/l)
------------|:----------:|:-------:|:--------:|:---------:
GluT1 | 3-7 mM | 3.84-5.09 nm | 3.62-8.43E+6 | 6.01-13.95
GluT3 | 1.4 mM | 6.57 nm | 1.68E+6 | 2.79
ID:(8456, 0)
Flujo No Saturado por Largo
Ecuación 
El flujo saturado por una membrana cilíndrica de radio R en que existe una concentración de bombas de glucosa C y en que el tiempo de re activación de la bomba es \tau se puede calcular mediante:
| j_s=\displaystyle\frac{2\pi R C}{\tau} |
En el caso más general se tiene que con una concentración c el número de moléculas a capturar son aquellas en la zona de radio r. En el caso de no existir saturación la concentración c debe ser menor que la concentración crítica:
| c_s=\displaystyle\frac{3}{2\pi}\displaystyle\frac{1}{r^3} |
Por ello el caso no saturado el flujo es
| j=\displaystyle\frac{c}{c_s}j_s |
ID:(8455, 0)
Flujos por GluTs (radial)
Descripción 
El flujo por una membrana en base a los transportadores se modela mediante
| J=\left(j_{si}\displaystyle\frac{c_i}{c_{si}}-j_{so}\displaystyle\frac{c_o}{c_{so}}\right)\Delta z |
Si se asume que el endotelio y el astrocito/lamina basal empela mayormente GluT1 y albumina/neurona con GluT3 se tienen los parámetros
Membranes | c_s (1/um3) | j_s (1/um s) | j_s/c_s (um2/s)
-----------------|:-----------------:|:------------------:|:-----------:
Endothelial | 6.02E+6 | 2.76E+5 | 0.0458
Atrocyte/Basal laminar | 6.02E+6 | 7.70E+4 | 0.0128
Abluminal/Neuron | 1.68E+6 | 5.90E+4 | 0.0351
En el caso del endotelio la concentración en la sangre es 3.41E+6 1/um3 lo que es menor que la concentración crítica de este.
Si no existe glucosa en el espacio entre endotelio y membrana basal el flujo del lumen estaría definido por la concentración en este último que es del orden de 3.41E+6 1/um3. Por ello el flujo será del orden de 1.56E+5 1/um s por cada um.
ID:(8547, 0)
Flujos por GluTs (radial), caso simétrico no saturado
Descripción 
Si el GluT opera en forma simétrica, o sea la probabilidad de transporte es igual en ambas direcciones, se tiene que c_{si}\sim c_{so}\sim c_s y j_{si}\sim j_{so}\sim j_s con lo que el flujo es
| J=\displaystyle\frac{j_s\Delta z}{c_s}(c_i-c_o) |
que es similar a una ecuación de Frick que describe la difusión. Se debe tener presente de que esta ecuación solo vale en el limite en que no se ha alcanzado la situación de saturación.
ID:(8853, 0)
Flujos por GluTs (radial), caso simétrico saturado
Descripción 
En el caso simetrico el GluT pasa a estar saturado si la concentración interna y externa sumada superan la concnetración de saturación
c_{si}+c_{so} > c_s
siendo en dicho caso el fujo el de un sistema saturado
| J=j_s\Delta z |
y ya no depende de la diferencia de concnetración.
ID:(8854, 0)
Resultados del Modelo
Imagen 
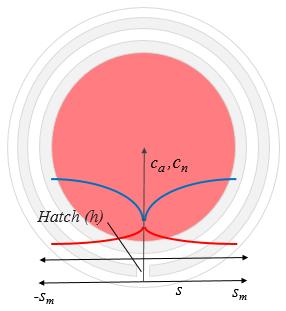
El modelo busca calcular la distribución de glucosa en los espacios entre endotelio y membrana basal c_e y entre membrana basal y neurona/astrocito c_b. La distribución se mide a lo largo del perímetro y se emplea como variable la distancia al la apertura (hatch) s:
ID:(8453, 0)
