Utilisateur:
Mécanismes
Iframe 
La clé pour décrire un mouvement à vitesse constante réside dans la compréhension des concepts de :
• Position,
• Déplacement,
• Temps et
• Temps écoulé,
pour définir la vitesse. Enfin, la représentation graphique et son interprétation sont discutées.
Mécanismes
ID:(15999, 0)
Position
Concept
A position ($s$) d'un objet dans un système unidimensionnel fait référence à l'emplacement de l'objet par rapport à un point de référence. Cette position est exprimée comme la distance entre l\'objet et le point d\'origine. Cette distance peut être une ligne droite sur un axe cartésien, ou elle peut suivre un chemin courbe.
Position le long d'une route suivant son axe
ID:(15, 0)
Position initiale
Concept
A vitesse ($s_0$) est l'emplacement de départ d'un objet avant que tout mouvement ne commence. Cette position est définie comme la distance entre l'objet et le point d\'origine. Cette distance peut être une ligne droite sur un axe cartésien ou elle peut suivre une trajectoire courbe.
Position initiale le long d'une route suivant son axe
ID:(10302, 0)
Distance parcourue
Concept
A distance parcourue en un temps ($\Delta s$) pour un objet est déterminé en mesurant la distance entre deux points spécifiques le long d'un trajet. Ce trajet peut être une ligne droite dans un repère cartésien ou une trajectoire courbe. La distance est calculée comme la longueur du chemin reliant les points de départ et d'arrivée.
Distance parcourue dun point initial à un point final
Comme la valeur de a distance parcourue en un temps ($\Delta s$) est calculée comme la différence entre a position ($s$) et a vitesse ($s_0$) :
| $ \Delta s \equiv s - s_0 $ |
il est possible de « déplacer » lorigine de la position en ajoutant une valeur constante $d$ aux deux grandeurs :
$s \rightarrow s + d$
$s_0 \rightarrow s_0 + d$
sans affecter le résultat de la distance parcourue :
$\Delta s = s - s_0 \rightarrow (s + d) - (s_0 + d) = s - s_0 = \Delta s$
Ce concept est appelé invariance spatiale, ce qui signifie que la valeur de la distance parcourue ne dépend pas du point spécifique où commence la mesure.
Cela implique que les lois formulées en utilisant ce principe seront invariantes spatiales, cest-à-dire quelles resteront valides quel que soit lendroit où la mesure est effectuée.
ID:(9495, 0)
Temps
Concept
L'évolution de tout système est décrite par différents paramètres, chacun évoluant selon une échelle appelée le temps ($t$).
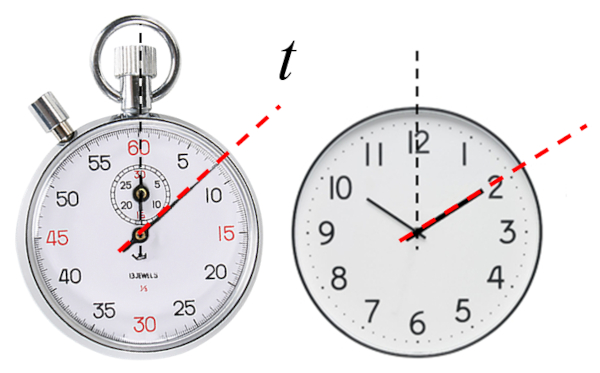
Heure indiquée par une horloge, soit la valeur à laquelle elle marque, soit l'heure
Traditionnellement, le temps était considéré comme absolu dans la physique classique, étant le même dans tous les systèmes de référence. Cependant, la théorie de la relativité a généralisé ce concept et doit maintenant être considéré comme unique pour chaque système de référence, pouvant différer dans son avancement.
ID:(478, 0)
Temps initial
Concept
Les systèmes sont invariants dans le temps, ce qui signifie que leur comportement n'est pas affecté par le moment où le processus commence. Cela nous permet de choisir le temps initial ($t_0$), en fonction de ce qui est le plus pratique. Cela pourrait être basé sur l'instrument utilisé pour mesurer le temps ou pour faciliter les calculs.
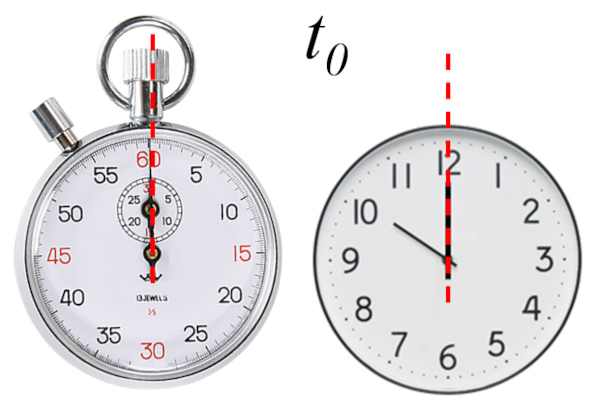
L'heure à laquelle commence la mesure, qu'elle soit fixe ou par système (chronomètre)
Au final, le moment de départ peut être choisi librement.
ID:(715, 0)
Temps écoulé
Concept
La base de la description de toute évolution est la définition du temps auquel elle est décrite. En particulier, on travaille avec le temps écoulé ($\Delta t$) depuis un temps de référence.
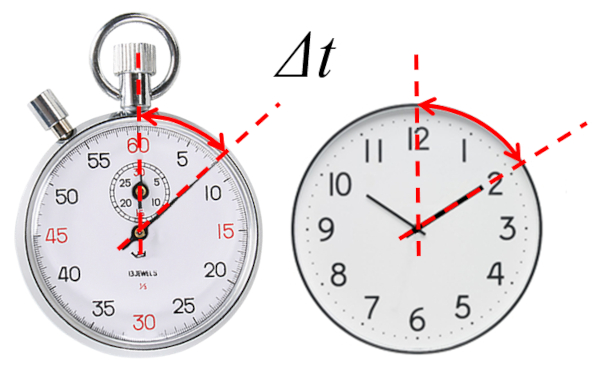
Le chronomètre nous indique directement le temps écoulé puisque son temps initial est zéro
Dans le cas d'un chronomètre, le temps écoulé est mesuré depuis le début de sa mesure, c'est-à-dire un temps initial nul ($t_0=0$).
Dans le cas de l'horloge, il est nécessaire de définir le type initial afin de déterminer le temps écoulé.
Dans le cas d'une montre, le temps écoulé est mesuré depuis un temps initial défini, qui peut être nul ou non.
Comme le temps écoulé ($\Delta t$) est calculé comme la différence entre le temps ($t$) et le temps initial ($t_0$) :
| $ \Delta t \equiv t - t_0 $ |
il est possible de « déplacer » lorigine du temps en ajoutant une valeur constante
aux deux magnitudes :
$t \rightarrow t + \tau$
$t_0 \rightarrow t_0 + \tau$
sans affecter le résultat du temps écoulé :
$\Delta t = t - t_0 \rightarrow (t + \tau) - (t_0 + \tau) = t - t_0 = \Delta t$
Ce concept est appelé invariance temporelle, ce qui signifie que la valeur du temps écoulé ne dépend pas du moment précis où commence la mesure.
Cela implique que les lois formulées en utilisant ce principe seront invariantes dans le temps, cest-à-dire quelles resteront valides quelles soient appliquées dans le présent, le passé ou le futur.
ID:(12507, 0)
Vitesse constante
Concept
A vitesse constante ($v_0$) peut être calculé à partir de a distance parcourue en un temps ($\Delta s$) et le temps écoulé ($\Delta t$) comme suit :
a distance parcourue en un temps ($\Delta s$) est mesuré ou calculé à partir des positions :
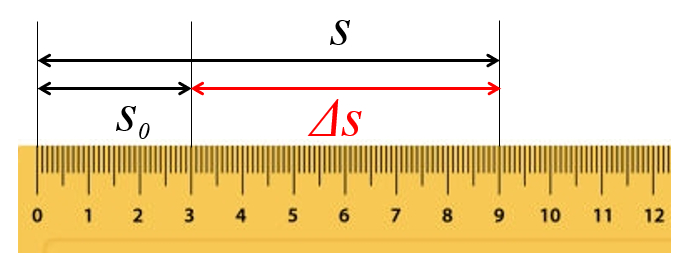
La distance parcourue est déterminée par les positions initiale et finale
Tandis que le temps écoulé ($\Delta t$) est mesuré ou calculé à partir du temps :
Le temps écoulé est déterminé par les instants initial et final
Cela permet de définir a vitesse constante ($v_0$) :
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
qui représente comment la distance est parcourue au fil du temps :
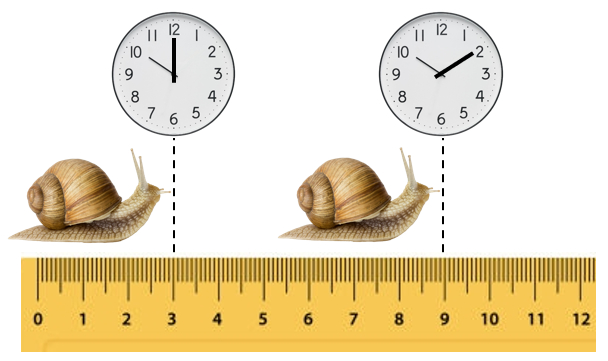
À partir de la distance parcourue et du temps écoulé, on obtient la vitesse
Dans l'exemple, la distance parcourue est $\Delta s =9 cm - 3 cm = 6 cm$, et le temps écoulé est $\Delta t = 10:10-10:00 = 10 min$. Ainsi, la vitesse est :
$v_0 = \displaystyle\frac{6\text{cm}}{10\text{min}} = 0.6\text{cm/min}$
Il est important de noter que, puisque $\Delta s$ est invariant spatialement et $\Delta t$ est invariant temporellement, la définition de la vitesse est à la fois invariante spatialement et temporellement, cest-à-dire quelle reste valable en tout lieu et à tout moment.
De plus, si le principe dinertie est appliqué, qui stipule que, en labsence de forces extérieures, la vitesse reste constante, cette invariance garantit la cohérence dans tous les scénarios.
ID:(16001, 0)
Modèle
Top
Le modèle de base relie a position ($s$), mesuré à partir d'un origine a vitesse ($s_0$), résultant en une distance parcourue en un temps ($\Delta s$), et le temps ($t$), mesuré à partir d'une origine le temps initial ($t_0$), résultant en le temps écoulé ($\Delta t$). À partir de ces différences, a vitesse constante ($v_0$) est défini.
La relation de base du modèle est la droite qui associe les variables centrales du modèle :
Avec cela, la structure en réseau du modèle est :
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ \Delta s \equiv s - s_0 $
Ds = s - s_0
$ \Delta t \equiv t - t_0 $
Dt = t - t_0
$ s = s_0 + v_0 ( t - t_0 )$
s = s_0 + v_0 *( t - t_0 )
$ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$
v_0 = Ds / Dt
ID:(15998, 0)
Distance parcourue
Équation
Nous pouvons calculer a distance parcourue en un temps ($\Delta s$) à partir de a vitesse ($s_0$) et a position ($s$) grâce à l'équation suivante :
| $ \Delta s \equiv s - s_0 $ |
ID:(4352, 0)
Temps écoulé
Équation
Pour décrire le mouvement d'un objet, nous devons calculer le temps écoulé ($\Delta t$). Cette grandeur est obtenue en mesurant le temps initial ($t_0$) et le le temps ($t$) de ce mouvement. La durée est déterminée en soustrayant le temps initial du temps final :
| $ \Delta t \equiv t - t_0 $ |
ID:(4353, 0)
Vitesse constante
Équation
A vitesse constante ($v_0$) peut être calculé à partir de a distance parcourue en un temps ($\Delta s$) et le temps écoulé ($\Delta t$) en utilisant :
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
ID:(16000, 0)
Position à vitesse constante
Équation
Si la vitesse est constante, la vitesse sera égale à A vitesse initiale ($v_0$). Dans ce cas, la distance parcourue en fonction du temps peut être calculée en utilisant la différence entre a position ($s$) et a vitesse ($s_0$), divisée par la différence entre le temps ($t$) et le temps initial ($t_0$) :
| $ s = s_0 + v_0 ( t - t_0 )$ |
Avec a distance parcourue en un temps ($\Delta s$) c'est avec a position ($s$) et a vitesse ($s_0$) :
| $ \Delta s \equiv s - s_0 $ |
et le temps écoulé ($\Delta t$) est avec le temps ($t$) et le temps initial ($t_0$) :
| $ \Delta t \equiv t - t_0 $ |
L'équation pour la vitesse moyenne :
L'équation correspondante définit une ligne droite dans l'espace-temps.
ID:(3154, 0)