Usuario:
Mecanismos
Iframe 
La clave del modelo para describir un movimiento a velocidad constante es comprender el concepto de
• posición,
• camino recorrido,
• tiempo y
• tiempo transcurrido
para definir la velocidad. Por ultimo se discute la representación grafica y su interpretación.
Mecanismos
ID:(15999, 0)
Posición
Concepto
La posición ($s$) de un objeto en un sistema unidimensional se refiere a la ubicación del objeto en relación con un punto de referencia. Esta ubicación se expresa como la distancia entre el objeto y el punto de origen. Esta distancia puede ser una línea recta en un eje cartesiano, o puede seguir un camino curvo:
Posición a lo largo de una carretera siguiendo el eje de esta
ID:(15, 0)
Posición inicial
Concepto
La posición inicial ($s_0$) es la ubicación inicial de un objeto antes de que comience un movimiento. Esta ubicación se define como la distancia entre el objeto y el punto de origen. Esta distancia puede ser una línea recta sobre un eje cartesiano, o puede seguir una trayectoria curva.
Posición inicial a lo largo de una carretera siguiendo el eje de esta
ID:(10302, 0)
Distancia recorrida
Concepto
La distancia recorrida en un tiempo ($\Delta s$) por un objeto se determina midiendo la distancia entre dos puntos específicos a lo largo de una trayectoria. Esta trayectoria puede ser una línea recta en un eje cartesiano o un camino curvo. La distancia se calcula como la longitud de la trayectoria que conecta los dos puntos inicial y final.
Distancia recorrida desde un punto inicial hasta un punto final
Como el valor de la distancia recorrida en un tiempo ($\Delta s$) se calcula como la diferencia entre la posición ($s$) y la posición inicial ($s_0$):
| $ \Delta s \equiv s - s_0 $ |
es posible "trasladar" el origen de la posición añadiendo un valor constante $d$ a ambas magnitudes:
$s \rightarrow s + d$
$s_0 \rightarrow s_0 + d$
sin afectar el resultado de la distancia recorrida:
$\Delta s = s - s_0 \rightarrow (s + d) - (s_0 + d) = s - s_0 = \Delta s$
Este concepto se conoce como invariancia espacial, lo que implica que el valor de la distancia recorrida no depende del punto específico desde el cual se inicia la medición.
Esto significa que las leyes formuladas utilizando este principio serán invariantes espaciales, es decir, serán válidas independientemente del lugar donde se realice la medición.
ID:(9495, 0)
Tiempo
Concepto
La evolución de cualquier sistema se describe mediante distintos parámetros, cada uno de ellos evolucionando en función de un escalar denominado el tiempo ($t$).
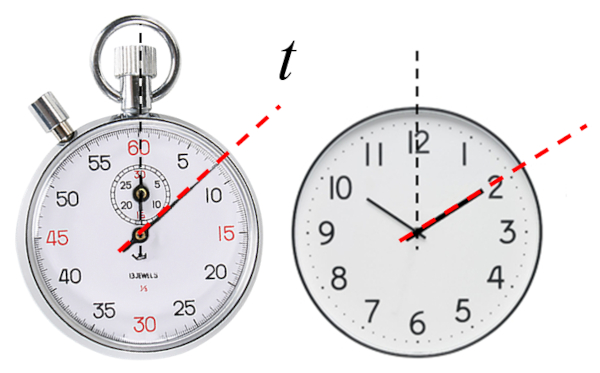
Tiempo que indica un reloj ya sea el valor en que se marca o la hora
Tradicionalmente, el tiempo se consideraba absoluto en la física clásica, siendo igual en todos los sistemas de referencia. No obstante, la teoría de la relatividad ha generalizado este concepto y ahora debe ser visto como propio de cada sistema de referencia, pudiendo diferir en su avance.
ID:(478, 0)
Tiempo inicial
Concepto
De esta forma, podemos fijar el tiempo inicial ($t_0$) según sea más conveniente para facilitar los cálculos. Esto puede ser hecho en función del instrumento con que se determina el tiempo, para asegurar la precisión de los resultados, o de manera teórica para simplificar los cálculos.
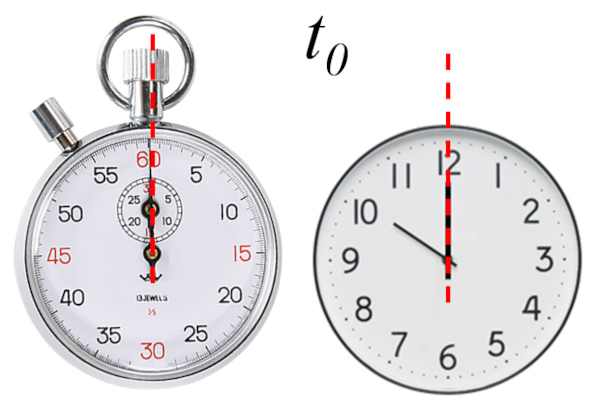
El tiempo en que se inicia la medición ya sea fijado o por sistema (cronómetro)
De esta forma, el tiempo inicial puede ser fijado libremente sin preocuparse por cambios en el resultado.
ID:(715, 0)
Tiempo transcurrido
Concepto
La base de la descripción de cualquier evolución es la definición del tiempo en que se describe. En particular, se trabaja con el tiempo transcurrido ($\Delta t$) desde un tiempo de referencia.
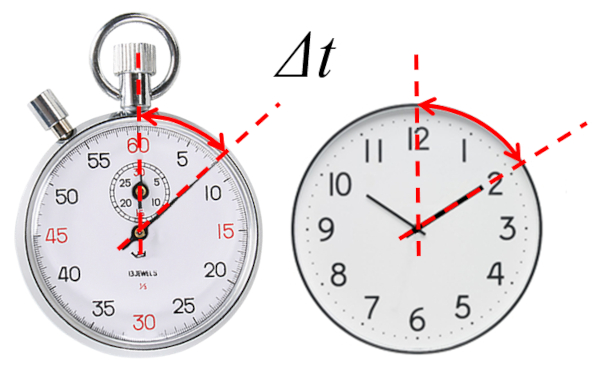
El cronometro nos entre directamente el tiempo transcurrido ya que su tiempo inicial es nulo
En el caso de un cronómetro, el tiempo transcurrido se mide desde el inicio de su medición, es decir, un tiempo inicial cero ($t_0=0$).
En el caso del reloj es necesario definir el tipo inicial para poder determinar el tiempo trascurrido.
En el caso de un reloj, el tiempo transcurrido se mide desde un tiempo inicial definido, que puede ser o no cero.
Como el tiempo transcurrido ($\Delta t$) se calcula como la diferencia entre el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
es posible "trasladar" el origen del tiempo sumando un valor constante
a ambas magnitudes:
$t \rightarrow t + \tau$
$t_0 \rightarrow t_0 + \tau$
sin afectar el resultado del tiempo transcurrido:
$\Delta t = t - t_0 \rightarrow (t + \tau) - (t_0 + \tau) = t - t_0 = \Delta t$
Este concepto se conoce como invariancia temporal, lo que implica que el valor del tiempo transcurrido no depende del momento específico en que se inicia la medición.
Esto significa que las leyes formuladas utilizando este principio serán invariantes temporales, es decir, serán válidas independientemente de si se aplican en el presente, en el pasado o en el futuro.
ID:(12507, 0)
Velocidad constante
Concepto
La velocidad constante ($v_0$) se puede calcular a partir de la distancia recorrida en un tiempo ($\Delta s$) y el tiempo transcurrido ($\Delta t$) de la siguiente manera:
la distancia recorrida en un tiempo ($\Delta s$) se mide o calcula a partir de las posiciones:
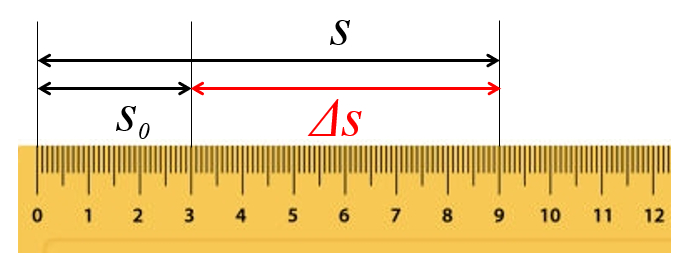
El camino recorrido se determina a partir de las posiciones inicial y final
Mientras que el tiempo transcurrido ($\Delta t$) se mide o calcula a partir del tiempo:
El tiempo transcurrido se determina a partir del tiempo inicial y final
Esto permite definir la velocidad constante ($v_0$):
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
que representa cómo se avanza en el tiempo:
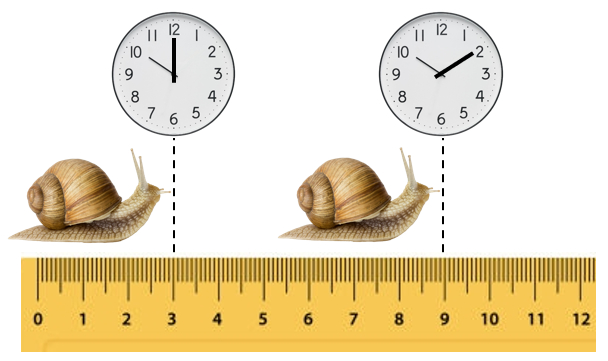
De la distancia recorrida y el tiempo transcurrido se obtiene la velocidad
En el ejemplo, la distancia recorrida es $\Delta s =9 cm - 3 cm = 6 cm$, y el tiempo transcurrido es $\Delta t = 10:10-10:00 = 10 min$. Por lo tanto, la velocidad es:
$v_0 = \displaystyle\frac{6\text{cm}}{10\text{min}} = 0.6\text{cm/min}$
Es importante notar que, dado que $\Delta s$ es invariante espacial y $\Delta t$ es invariante temporal, la definición de velocidad es tanto invariante espacial como temporal, es decir, es válida en cualquier lugar y momento.
Además, si se aplica el principio de inercia, que establece que en ausencia de fuerzas externas la velocidad permanece constante, esta invariancia garantiza la coherencia en todos los escenarios.
ID:(16001, 0)
Modelo
Top
El modelo base relaciona la posición ($s$), medido desde un origen la posición inicial ($s_0$), lo que resulta en una distancia recorrida en un tiempo ($\Delta s$), y el tiempo ($t$), medido desde un origen el tiempo inicial ($t_0$), lo que da el tiempo transcurrido ($\Delta t$). A partir de estas diferencias, se define la velocidad constante ($v_0$).
La relación base del modelo es la recta que asocia las variables centrales del modelo:
Con esto, la estructura de red del modelo es la siguiente:
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ \Delta s \equiv s - s_0 $
Ds = s - s_0
$ \Delta t \equiv t - t_0 $
Dt = t - t_0
$ s = s_0 + v_0 ( t - t_0 )$
s = s_0 + v_0 *( t - t_0 )
$ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$
v_0 = Ds / Dt
ID:(15998, 0)
Distancia recorrida
Ecuación
Podemos calcular la distancia recorrida en un tiempo ($\Delta s$) a partir de la posición inicial ($s_0$) y la posición ($s$) mediante la siguiente ecuación:
| $ \Delta s \equiv s - s_0 $ |
ID:(4352, 0)
Tiempo transcurrido
Ecuación
Para describir el movimiento de un objeto, debemos calcular el tiempo transcurrido ($\Delta t$). Esta magnitud se obtiene midiendo el tiempo inicial ($t_0$) y el el tiempo ($t$) de dicho movimiento. La duración se determina restando el tiempo inicial al tiempo final:
| $ \Delta t \equiv t - t_0 $ |
ID:(4353, 0)
Velocidad constante
Ecuación
La velocidad constante ($v_0$) se puede calcular de la distancia recorrida en un tiempo ($\Delta s$) y el tiempo transcurrido ($\Delta t$) mediante:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
ID:(16000, 0)
Posición con velocidad constante
Ecuación
Si la velocidad es constante, la velocidad será igual a la velocidad inicial ($v_0$). En este caso, el camino recorrido en función del tiempo puede calcularse utilizando la diferencia entre la posición ($s$) y la posición inicial ($s_0$), dividida por la diferencia entre el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ s = s_0 + v_0 ( t - t_0 )$ |
Con la distancia recorrida en un tiempo ($\Delta s$) es con la posición ($s$) y la posición inicial ($s_0$):
| $ \Delta s \equiv s - s_0 $ |
y el tiempo transcurrido ($\Delta t$) es con el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
Se tiene que la ecuación de la velocidad media:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
puede escribirse como:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
Por lo tanto, despejando, se obtiene:
| $ s = s_0 + v_0 ( t - t_0 )$ |
La ecuación correspondiente define una línea recta en el espacio-tiempo.
ID:(3154, 0)