Benützer:
Mechanismen
Iframe 
Der Schlüssel zur Beschreibung einer Bewegung mit konstanter Geschwindigkeit liegt im Verständnis der Konzepte von:
• Position,
• zurückgelegter Weg,
• Zeit und
• vergangener Zeit,
um die Geschwindigkeit zu definieren. Schließlich wird die grafische Darstellung und deren Interpretation diskutiert.
Mechanismen
ID:(15999, 0)
Position
Konzept
Die Position ($s$) eines Objekts in einem eindimensionalen System bezieht sich auf den Standort des Objekts in Bezug auf einen Referenzpunkt. Diese Lage wird als Entfernung zwischen dem Objekt und dem Ursprungspunkt ausgedrückt. Diese Entfernung kann eine Gerade auf einem kartesischen Koordinatensystem sein oder einem gekrümmten Pfad folgen.
Position entlang einer Straße entlang ihrer Achse
ID:(15, 0)
Ausgangsposition
Konzept
Die Ausgangsstellung ($s_0$) ist der Startort eines Objekts, bevor sich dieses bewegt. Diese Position wird als Entfernung zwischen dem Objekt und dem Ursprungspunkt definiert. Diese Entfernung kann eine Gerade auf einem kartesischen Koordinatensystem sein oder einem gekrümmten Pfad folgen.
Anfangsposition entlang einer Straße, die ihrer Achse folgt
ID:(10302, 0)
Zurückgelegte Strecke
Konzept
Die Zurückgelegte Strecke in einer Zeit ($\Delta s$) wird für ein Objekt bestimmt, indem die Entfernung zwischen zwei bestimmten Punkten entlang eines Pfads gemessen wird. Dieser Pfad kann eine gerade Linie in einem kartesischen Koordinatensystem oder eine gekrümmte Bahn sein. Die Entfernung wird als die Länge des Pfads berechnet, der die Anfangs- und Endpunkte verbindet.
Zurückgelegte Strecke von einem Anfangspunkt zu einem Endpunkt
Da der Wert von die Zurückgelegte Strecke in einer Zeit ($\Delta s$) als die Differenz zwischen die Position ($s$) und die Ausgangsstellung ($s_0$) berechnet wird:
| $ \Delta s \equiv s - s_0 $ |
ist es möglich, den Ursprung der Position zu verschieben, indem ein konstanter Wert $d$ zu beiden Größen addiert wird:
$s \rightarrow s + d$
$s_0 \rightarrow s_0 + d$
ohne das Ergebnis der zurückgelegten Strecke zu beeinflussen:
$\Delta s = s - s_0 \rightarrow (s + d) - (s_0 + d) = s - s_0 = \Delta s$
Dieses Konzept wird als räumliche Invarianz bezeichnet, was bedeutet, dass der Wert der zurückgelegten Strecke nicht davon abhängt, wo genau die Messung beginnt.
Das bedeutet, dass die mit diesem Prinzip formulierten Gesetze räumlich invariant sind, das heißt, sie gelten unabhängig davon, wo die Messung durchgeführt wird.
ID:(9495, 0)
Zeit
Konzept
Die Entwicklung jedes Systems wird durch verschiedene Parameter beschrieben, die jeweils nach einer Skala, der Zeit ($t$), entwickeln.
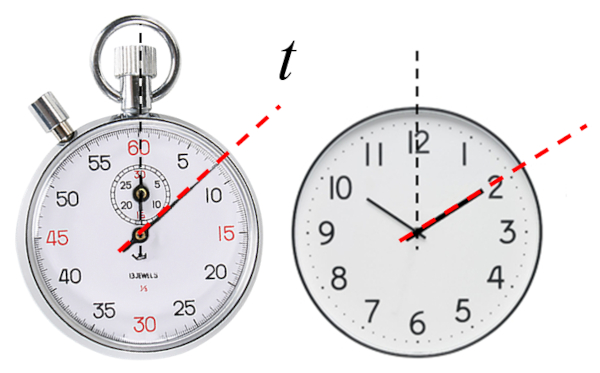
Zeit, die von einer Uhr angezeigt wird, entweder der Wert, den sie markiert, oder die Zeit
Traditionell wurde Zeit in der klassischen Physik als absolut betrachtet, gleich in allen Referenzsystemen. Die Relativitätstheorie hat diesen Begriff jedoch verallgemeinert und er muss nun als einzigartig für jedes Referenzsystem angesehen werden, das in seiner Entwicklung unterschiedlich sein kann.
ID:(478, 0)
Anfangszeit
Konzept
Systeme sind zeitinvariant, was bedeutet, dass ihr Verhalten nicht von dem Zeitpunkt abhängt, wann der Prozess beginnt. Dies ermöglicht es uns, der Startzeit ($t_0$), auf das Bequemste zu wählen. Dies könnte auf dem Instrument basieren, das verwendet wird, um die Zeit zu messen oder die Berechnungen zu erleichtern.
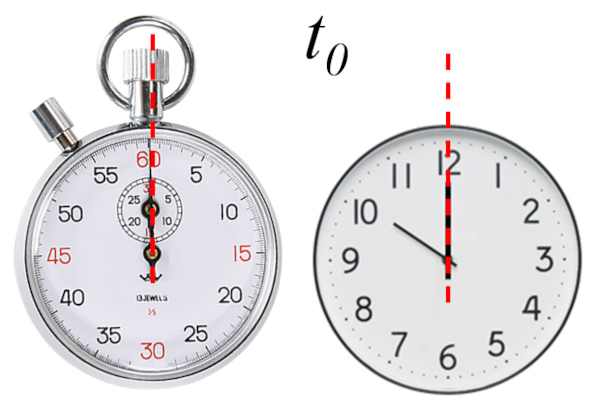
Der Zeitpunkt, zu dem die Messung beginnt, ob fest oder nach System (Chronometer)
Letztendlich kann der Beginnzeitpunkt frei gewählt werden.
ID:(715, 0)
Verstrichene Zeit
Konzept
Die Grundlage für die Beschreibung jeder Entwicklung ist die Definition der Zeit, in der sie beschrieben wird. Insbesondere wird mit der Abgelaufene Zeit ($\Delta t$) seit einem Referenzzeitpunkt gearbeitet.
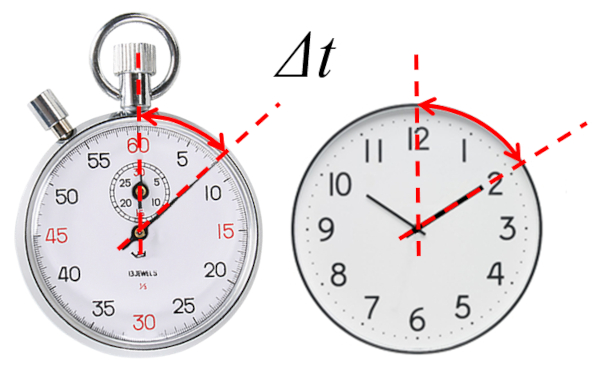
Die Stoppuhr zeigt uns direkt die verstrichene Zeit an, seit ihre Anfangszeit Null ist
Im Falle eines Stoppuhrs wird die verstrichene Zeit seit Beginn der Messung gemessen, d.h. eine Null-Startzeit ($t_0=0$).
Im Fall der Uhr ist es notwendig, den Anfangstyp zu definieren, um die verstrichene Zeit zu bestimmen.
Im Falle einer Uhr wird die verstrichene Zeit seit einem definierten Startzeitpunkt gemessen, der null oder ungleich null sein kann.
Da der Abgelaufene Zeit ($\Delta t$) als die Differenz zwischen der Zeit ($t$) und der Startzeit ($t_0$) berechnet wird:
| $ \Delta t \equiv t - t_0 $ |
ist es möglich, den Zeitursprung zu "verschieben", indem ein konstanter Wert
zu beiden Größen hinzugefügt wird:
$t \rightarrow t + \tau$
$t_0 \rightarrow t_0 + \tau$
ohne das Ergebnis der verstrichenen Zeit zu beeinflussen:
$\Delta t = t - t_0 \rightarrow (t + \tau) - (t_0 + \tau) = t - t_0 = \Delta t$
Dieses Konzept wird als zeitliche Invarianz bezeichnet, was bedeutet, dass der Wert der verstrichenen Zeit unabhängig vom spezifischen Startpunkt der Messung unverändert bleibt.
Dies bedeutet, dass die mit diesem Prinzip formulierten Gesetze zeitlich invariant sind, d. h., sie gelten unabhängig davon, ob sie in der Gegenwart, der Vergangenheit oder der Zukunft angewendet werden.
ID:(12507, 0)
Konstante Geschwindigkeit
Konzept
Die Konstante Geschwindigkeit ($v_0$) kann aus die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) wie folgt berechnet werden:
die Zurückgelegte Strecke in einer Zeit ($\Delta s$) wird gemessen oder berechnet aus den Positionen:
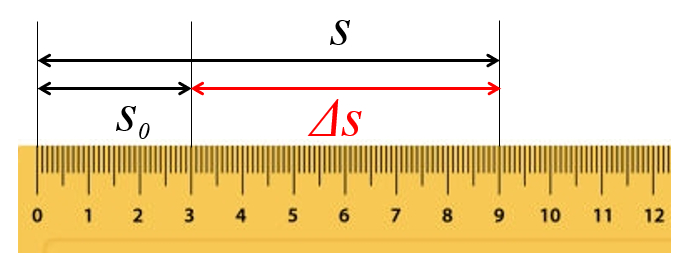
Die zurückgelegte Strecke wird aus den Anfangs- und Endpositionen bestimmt
Während der Abgelaufene Zeit ($\Delta t$) aus der Zeit gemessen oder berechnet wird:
Die verstrichene Zeit wird aus der Anfangs- und Endzeit bestimmt
Daraus lässt sich die Konstante Geschwindigkeit ($v_0$) definieren:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
was beschreibt, wie sich die Strecke über die Zeit verändert:
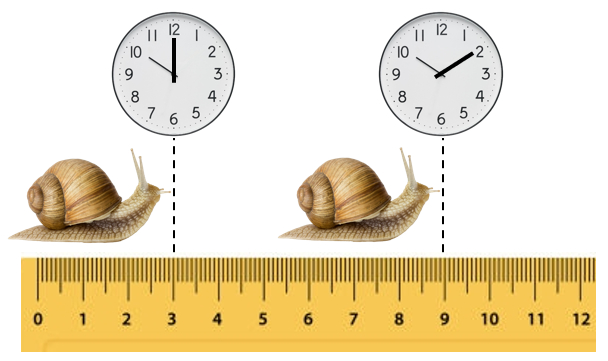
Aus der zurückgelegten Strecke und der verstrichenen Zeit ergibt sich die Geschwindigkeit
Im Beispiel ist die zurückgelegte Strecke $\Delta s =9 cm - 3 cm = 6 cm$, und die verstrichene Zeit beträgt $\Delta t = 10:10-10:00 = 10 min$. Somit ergibt sich die Geschwindigkeit:
$v_0 = \displaystyle\frac{6\text{cm}}{10\text{min}} = 0.6\text{cm/min}$
Es ist wichtig zu beachten, dass, da $\Delta s$ räumlich invariant ist und
$\Delta t$ zeitlich invariant ist, die Definition der Geschwindigkeit sowohl räumlich als auch zeitlich invariant ist, das heißt, sie gilt an jedem Ort und zu jeder Zeit.
Wenn zusätzlich das Trägheitsprinzip gilt, das besagt, dass die Geschwindigkeit konstant bleibt, solange keine äußeren Kräfte wirken, garantiert diese Invarianz die Konsistenz in allen Szenarien.
ID:(16001, 0)
Modell
Top
Das Basismodell bezieht sich auf die Position ($s$), gemessen von einem Ursprung die Ausgangsstellung ($s_0$), was zu eine Zurückgelegte Strecke in einer Zeit ($\Delta s$) führt, und der Zeit ($t$), gemessen von einem Ursprung der Startzeit ($t_0$), was zu der Abgelaufene Zeit ($\Delta t$) führt. Aus diesen Differenzen ergibt sich die Konstante Geschwindigkeit ($v_0$) entspricht.
Die Basisbeziehung des Modells ist die Gerade, die die zentralen Variablen des Modells verbindet:
Damit ist die Netzwerkstruktur des Modells:
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ \Delta s \equiv s - s_0 $
Ds = s - s_0
$ \Delta t \equiv t - t_0 $
Dt = t - t_0
$ s = s_0 + v_0 ( t - t_0 )$
s = s_0 + v_0 *( t - t_0 )
$ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$
v_0 = Ds / Dt
ID:(15998, 0)
Zurückgelegten Strecke
Gleichung
Wir können die Zurückgelegte Strecke in einer Zeit ($\Delta s$) aus die Ausgangsstellung ($s_0$) und die Position ($s$) berechnen mit der folgenden Gleichung:
| $ \Delta s \equiv s - s_0 $ |
ID:(4352, 0)
Verstrichenen Zeit
Gleichung
Um die Bewegung eines Objekts zu beschreiben, müssen wir der Abgelaufene Zeit ($\Delta t$) berechnen. Diese Größe wird durch Messung von der Startzeit ($t_0$) und der der Zeit ($t$) dieser Bewegung erhalten. Die Dauer wird bestimmt, indem die Anfangszeit von der Endzeit subtrahiert wird:
| $ \Delta t \equiv t - t_0 $ |
ID:(4353, 0)
Konstante Geschwindigkeit
Gleichung
Die Konstante Geschwindigkeit ($v_0$) kann aus die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) berechnet werden mit:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
ID:(16000, 0)
Fall von konstante Geschwindigkeit
Gleichung
Wenn die Geschwindigkeit konstant ist, wird die Geschwindigkeit gleich die Anfangsgeschwindigkeit ($v_0$) sein. In diesem Fall kann der zurückgelegte Weg in Abhängigkeit von der Zeit berechnet werden, indem die Differenz zwischen die Position ($s$) und die Ausgangsstellung ($s_0$) durch die Differenz zwischen der Zeit ($t$) und der Startzeit ($t_0$) geteilt wird:
| $ s = s_0 + v_0 ( t - t_0 )$ |
Mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) gleich die Position ($s$) und die Ausgangsstellung ($s_0$):
| $ \Delta s \equiv s - s_0 $ |
und der Abgelaufene Zeit ($\Delta t$) ist gleich der Zeit ($t$) und der Startzeit ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
Die Gleichung für die durchschnittliche Geschwindigkeit:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
kann geschrieben werden als:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
somit ergibt sich, wenn man nach ihr auflöst:
| $ s = s_0 + v_0 ( t - t_0 )$ |
Die entsprechende Gleichung definiert eine gerade Linie im Raum-Zeit-Kontinuum.
ID:(3154, 0)