Freie Weg von mehreren Partikeln
Beschreibung 
Wenn Sie die freien Wege für Photonen, Neutronen, Elektronen und Protonen im Wasser vergleichen, beobachten Sie Unterschiede in Zehnerpotenzen:
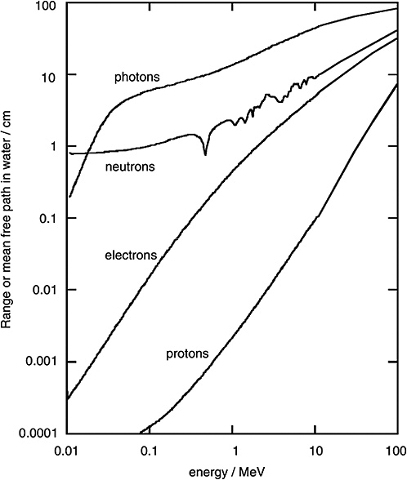
Freier Weg von Partikeln in Wasser (ICRU-Bericht von 1970).
In diesem Fall werden die Werte in Zentimetern angegeben. Für den Bereich von bis zu 0,01 bis 6 MeV sind die Bereiche (in cm)Partikel | 0,01 MeV | 6 MeV------------- |: ------------: |: ----------:Photonen | 0.198 | 41.7Neutronen | 0,878 | 0.430Elektronen | 0.00032 | 0.211Protonen | - | 0,033
ID:(9257, 0)
Freier Weg eines Photons
Beschreibung 
Wenn der freie Weg als eine Funktion der Dichte dargestellt wird, kann er zwischen verschiedenen Materialien verglichen werden. Als eine Funktion der Energie des Photons wird erreicht, dass der freie Weg in Knochen und Wasser im Bereich von 0 bis 10MeV sehr ähnlich ist:

Weg frei von Photonen in Wasser und Knochen. Der EGS4 Code System Report SLAC-265, Nelson W.R. et. al., Stanford Linear Accelerator Center, Kalifornien, 1985
Wenn eine Abschätzung der freien Weglänge des Photons in Wasser erwünscht ist, die ein dem Gewebe sehr ähnliches Verhalten zeigt, genügt es, die Länge in Gramm pro Quadratzentimeter mit der Dichte zu multiplizieren, mit der Werte zwischen 0 und 30 cm erhalten werden.
ID:(9256, 0)
Codestruktur (1)
Beschreibung 
Die Struktur des Simulationscodes muss aus drei Grundeinheiten bestehen:- die Definition der Verteilungsfunktion (die Anordnung, die Kugeln in der Galton-Tabelle sammelt)- der Simulator des Fortschritts des Teilchens, das die endgültige Position liefert- die Einheit, die die Klasse bestimmt, die in der Verteilungsfunktion erhöht werden muss (die Einheit, die bestimmt, in welchem ??Container des Empfängers von Kugeln diese abgelegt wird)Für den ersten Punkt müssen wir eine Anordnung definieren, die anfänglich auf Null gesetzt wird und schließlich entsprechend der erreichten Position besiedelt wird.Für den ersten Schritt müssen wir zuerst den Bereich definieren, in den die Kugel fällt, dh einen Minimalwert
ID:(9250, 0)
Codestruktur (2)
Beschreibung 
Um die endgültigen Positionen zu berechnen, müssen Sie:- über mehrere Partikel iterieren (N)- Für jede Partikelschätzung die gefahrenen Straßen- Fügen Sie die Straßen hinzu, die die Ausbreitungsrichtungen abwechselnIn diesem Fall wird angenommen, dass das Teilchen bei jeder Kollision seine Ausbreitungsrichtung ändert. Zu Beginn fängt es immer an zu reisen und vergrößert den Abstand, der als positive Richtung definiert ist (dir = 1). Bei jedem Absturz wird das dir-Zeichen invertiert (dir = -dir oder dir = 1, dies wird dir = -1).Für die Länge des Schritts wird die zuvor definierte Längenerzeugungsfunktion (exprob) aufgerufen, die mit der Adresse gewichtet wird, um die neue Position mit der vorherigen Position zu erhalten.```// particles (n de N)for(n = 0;n < N;n++){ x = 0; // initial position dir = 1; // initial direction for(i = 0;i < sp;i++){ x = x + dir*exprob(len); // new position dir = -dir; // change direction } // finish position calculation // clasification of end position x in distribution p}```
ID:(9258, 0)
Simulador random walk paso variable
Beschreibung 
Um die Verteilung der Positionen der Teilchen zu erhalten, kann folgende Iterationen durchgeführt werden```0. Position und Startadresse definiert1. Partikel in eine Richtung bewegen in einem Abstand der durch die Zufallswahrscheinlichkeitsfunktion erzeugt wird,2. Richtung umkehren3. Fortsetzung 1```Angenommen, wir eine bestimmte Zeit und das sich das Teilchen mit einer konstanten Geschwindigkeit bewegt. Somit kam die Position nach einer Zeit oder einem zurück gelegten Weg bestimmt werden.
ID:(9100, 0)
Zusammenfassung
Beschreibung 
Mit dem Simulator zu spielen, haben wir das bemerkt```1. Es ist nur sinnvoll, Verteilungen von möglichen Positionen zu betrachten2. Die Verteilung basiert auf der Bestimmung von Positionen in diskreten Bereichen3. Bereiche kleinerer Größe erfordern eine größere Anzahl von Iterationen```
ID:(9101, 0)
Modellierung mit homogenem Material (1D)
Beschreibung 
Variablen
Berechnungen
Berechnungen
Gleichungen
(ID 9255)
Beispiele
Der einfachste Fall ist der einer Partikel die sich entlang einer Achse bewegt und die nach einem Zusammensto mit einem Objekt die Bewegungsrichtung umkehrt.
Wenn die Wahrscheinlichkeit ein Abstand zwischen
Falls diese Wahrscheinlichkeit proportional zur Wahrscheinlichkeit
So folgt, dass
| $p(x)dx = \displaystyle\frac{1}{\lambda}e^{-x/\lambda}dx$ |
wobei
(ID 9099)
Wenn die Verteilung integriert ist
| $p(x)dx = \displaystyle\frac{1}{\lambda}e^{-x/\lambda}dx$ |
ber alle m glichen Entfernungen
| $\displaystyle\int_0^{\infty}p(x)dx = \displaystyle\int_0^{\infty}\displaystyle\frac{1}{\lambda}e^{-x/\lambda}dx=1$ |
was bedeutet, dass die Funktion normalisiert ist. Dies ist nicht berraschend, da die Funktion
(ID 9251)
Wenn Sie die freien Wege f r Photonen, Neutronen, Elektronen und Protonen im Wasser vergleichen, beobachten Sie Unterschiede in Zehnerpotenzen:

Freier Weg von Partikeln in Wasser (ICRU-Bericht von 1970).
In diesem Fall werden die Werte in Zentimetern angegeben. F r den Bereich von bis zu 0,01 bis 6 MeV sind die Bereiche (in cm)Partikel | 0,01 MeV | 6 MeV------------- |: ------------: |: ----------:Photonen | 0.198 | 41.7Neutronen | 0,878 | 0.430Elektronen | 0.00032 | 0.211Protonen | - | 0,033
(ID 9257)
Wenn der freie Weg als eine Funktion der Dichte dargestellt wird, kann er zwischen verschiedenen Materialien verglichen werden. Als eine Funktion der Energie des Photons wird erreicht, dass der freie Weg in Knochen und Wasser im Bereich von 0 bis 10MeV sehr hnlich ist:

Weg frei von Photonen in Wasser und Knochen. Der EGS4 Code System Report SLAC-265, Nelson W.R. et. al., Stanford Linear Accelerator Center, Kalifornien, 1985
Wenn eine Absch tzung der freien Wegl nge des Photons in Wasser erw nscht ist, die ein dem Gewebe sehr hnliches Verhalten zeigt, gen gt es, die L nge in Gramm pro Quadratzentimeter mit der Dichte zu multiplizieren, mit der Werte zwischen 0 und 30 cm erhalten werden.
(ID 9256)
Die Struktur des Simulationscodes muss aus drei Grundeinheiten bestehen:- die Definition der Verteilungsfunktion (die Anordnung, die Kugeln in der Galton-Tabelle sammelt)- der Simulator des Fortschritts des Teilchens, das die endg ltige Position liefert- die Einheit, die die Klasse bestimmt, die in der Verteilungsfunktion erh ht werden muss (die Einheit, die bestimmt, in welchem ??Container des Empf ngers von Kugeln diese abgelegt wird)F r den ersten Punkt m ssen wir eine Anordnung definieren, die anf nglich auf Null gesetzt wird und schlie lich entsprechend der erreichten Position besiedelt wird.F r den ersten Schritt m ssen wir zuerst den Bereich definieren, in den die Kugel f llt, dh einen Minimalwert
(ID 9250)
Um den Weg zu simulieren, m ssen wir in der Lage sein, die freien Weg gr ndet auf der Verteilung zuf llig zu erzeugen
| $p(x)dx = \displaystyle\frac{1}{\lambda}e^{-x/\lambda}dx$ |
Um dies zu tun, ist es ausreichend, die Wahrscheinlichkeit zu berechnen, einen Pfad
und l sche den Weg
| $x=-\lambda\ln(1-P)$ |
Wir erhalten eine Gleichung, die, wenn wir zuf llig eine Zahl zwischen 0 und 1 erzeugen, einen Pfad
(ID 9255)
Um die endg ltigen Positionen zu berechnen, m ssen Sie:- ber mehrere Partikel iterieren (N)- F r jede Partikelsch tzung die gefahrenen Stra en- F gen Sie die Stra en hinzu, die die Ausbreitungsrichtungen abwechselnIn diesem Fall wird angenommen, dass das Teilchen bei jeder Kollision seine Ausbreitungsrichtung ndert. Zu Beginn f ngt es immer an zu reisen und vergr ert den Abstand, der als positive Richtung definiert ist (dir = 1). Bei jedem Absturz wird das dir-Zeichen invertiert (dir = -dir oder dir = 1, dies wird dir = -1).F r die L nge des Schritts wird die zuvor definierte L ngenerzeugungsfunktion (exprob) aufgerufen, die mit der Adresse gewichtet wird, um die neue Position mit der vorherigen Position zu erhalten.```// particles (n de N)for(n = 0;n < N;n++){ x = 0; // initial position dir = 1; // initial direction for(i = 0;i < sp;i++){ x = x + dir*exprob(len); // new position dir = -dir; // change direction } // finish position calculation // clasification of end position x in distribution p}```
(ID 9258)
Um die Verteilung der Positionen der Teilchen zu erhalten, kann folgende Iterationen durchgef hrt werden```0. Position und Startadresse definiert1. Partikel in eine Richtung bewegen in einem Abstand der durch die Zufallswahrscheinlichkeitsfunktion erzeugt wird,2. Richtung umkehren3. Fortsetzung 1```Angenommen, wir eine bestimmte Zeit und das sich das Teilchen mit einer konstanten Geschwindigkeit bewegt. Somit kam die Position nach einer Zeit oder einem zur ck gelegten Weg bestimmt werden.
(ID 9100)
Mit dem Simulator zu spielen, haben wir das bemerkt```1. Es ist nur sinnvoll, Verteilungen von m glichen Positionen zu betrachten2. Die Verteilung basiert auf der Bestimmung von Positionen in diskreten Bereichen3. Bereiche kleinerer Gr e erfordern eine gr ere Anzahl von Iterationen```
(ID 9101)
ID:(1129, 0)
