Storyboard

El método de celdas de Boltzmann (Lattice Boltzmann Method - LBM) fue creado para reducir el tiempo de procesamiento en la solución de problemas hidro y aerodinámicos. En vez de resolver la ecuación diferencial de Navier Stokes, usa una representación equivalente basada en la ecuación de transporte de Boltzmann y reduce el esfuerzo de procesamiento trabajando con un espacio de fase discreto simplificado. El resultado es un simulador de alta velocidad capaz de describir procesos de alta complejidad.

>Modelo

ID:(1162, 0)

Ecuación

>Top, >Modelo

La función de Boltzmann describe el transporte de un sistema de partículas descrito por la función de distribución de velocidades:

donde el termino C describe la interacción (colisiones) entre estas.

ID:(8462, 0)

Ecuación

>Top, >Modelo

Si los parámetros se calculan con\\n\\n

$\chi = m c(\vec{x},t)$

y se promedia sobre la velocidad mediante

se obtiene mediante la masa la estimación de la densidad mediante:

ID:(8458, 0)

Ecuación

>Top, >Modelo

Si los parámetros se calculan con\\n\\n

$\chi_k = v_k$

promediando sobre la velocidad mediante

\\n\\ny con\\n\\n

$c(\vec{x},t)=\displaystyle\frac{1}{m}\rho(\vec{x},t)$

la velocidad del flujo se calcula integrando la función distribución de velocidad sobre todas las velocidades ponderando sobre las velocidades:

ID:(8459, 0)

Ecuación

>Top, >Modelo

Con el teorema de equipartición en que\\n\\n

$\displaystyle\frac{1}{2}m\vec{v}\cdot\vec{v}=\displaystyle\frac{3}{2}k_B T$

\\n\\ncon el parámetro se calculan con\\n\\n

$\chi = T = \displaystyle\frac{m\vec{v}\cdot\vec{v}}{3k_B}=\displaystyle\frac{\vec{v}\cdot\vec{v}}{3R}\displaystyle\frac{c(\vec{x},t)}{\rho(\vec{x},t)}$

y se promedia promediando sobre la velocidad mediante

y se considera el teorema de equipartición, la temperatura se podrá estimar integrando la energía cinética ponderada por la distribución de velocidad dividida por la constante de los gases:

ID:(8460, 0)

Ecuación

>Top, >Modelo

Si los parámetros se calculan con\\n\\n

$\chi = m c(\vec{x},t)(v_i-u_i)(v_j-u_j)$

y se promedia sobre la velocidad mediante

el tensor del flujo se calcula integrando la función distribución de velocidad sobre todas las velocidades ponderando sobre las diferencias de velocidades:

ID:(8461, 0)

Descripción

>Top

La problemática con sistemas en escala macro que se basan en fenómenos microscópicos es que

- los modelos macroscópicos son demasiado simples para reflejar correctamente la dinámica

- los modelos microscópicos para describir la realidad macroscópica no se pueden resolver analítica y las soluciones numéricas son engorrosas (= exigen muchos recursos computacionales)

El método de celdas de Boltzmann busca un camino intermedio. Se basa en la ecuación de transporte de Boltzmann, rescata de la parte microscópica vía el termino de colisiones e implementa una estructura simplificada para calcular los resultados macroscópicos. Hablamos de un enfoque mesoscopico en que podemos, según se requiera, reducir el esfuerzo microscópico perdiendo precisión pero ahorrando recursos o mejorando la precisión invirtiendo mas recursos.

ID:(8488, 0)

Imagen

>Top

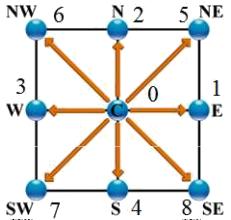
El modelo D2Q9 es un modelo bidimensional (D2) en que se se conecta el nodo (punto central) en nodos a lo largo de los ejes cartesianos\\n\\nen el origen\\n\\n

$\vec{e}_0=(0,0)$

\\n\\nen las esquinas\\n\\n

$\vec{e}_1=(1,0)$

(E),\\n

$\vec{e}_2=(0,1)$

(N), \\n

$\vec{e}_3=(-1,0)$

(W) y \\n

$\vec{e}_4=(0,-1)$

(S)\\n\\ny en las diagonales\\n\\n

$\vec{e}_5=(1,1)$

(NE), \\n

$\vec{e}_6=(-1,1)$

(SE), \\n

$\vec{e}_7=(-1,-1)$

(SW) y \\n

$\vec{e}_8=(1,-1)$

(NW)

lo que se representa en la siguiente gráfica:

ID:(8496, 0)

Imagen

>Top

El modelo D3Q15 es un modelo bidimensional (D3) en que se se conecta el nodo (punto central) en nodos a lo largo de los ejes cartesianos\\n\\n

$(1,0,0), (-1,0,0), (0,1,0), (0,-1,0), (0,0,1) y (0,0,-1)$

\\n\\ny en las esquinas del cubo\\n\\n

$(1,0,1), (-1,0,1), (0,1,1) , (0,-1,1), (1,0,-1), (-1,0,-1), (0,1,-1) , (0,-1,-1)$

lo que se representa en la siguiente gráfica:

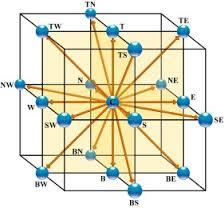
Es facil que se pueden construir modelos del tipo D3Q19 (incluyendo las mitades de las aristas laterales) o D3Q27 (todos los puntos posibles).

ID:(8497, 0)

Ecuación

>Top, >Modelo

En el caso de la discretización en los modelos LBM se trabaja no con funciones de la velocidad si no que con componentes discretas. De esta forma se define la componente i mediante:

en donde w_i es el peso relativo.

ID:(8466, 0)

Ecuación

>Top, >Modelo

En el proceso de streaming se desplazan las partículas según sus direcciones de velocidades a las celdas vecinas

donde \vec{x} es la posición, t el tiempo, \delta t el incremento en el tiempo, \vec{e}_i la dirección de la grilla y c la velocidad.

ID:(9150, 0)

Imagen

>Top

Si el choque no ocurre en el punto de la red si no que a una distancia \Delta:

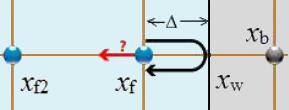
\\n\\nentonces la función debe considerar el desfase ponderando las contribuciones\\n\\n

$f_i(x_f,t+\delta t)=\displaystyle\frac{(1-\Delta)f_{-i}(x_f,t)+\Delta(f_{-i}(x_b,t)+f_{-i}(x_{f2},t)}{1+\Delta}$

ID:(8499, 0)

Imagen

>Top

Si la pared muestra una inclinación respecto de la red debe ser modelada en una forma mas compleja:

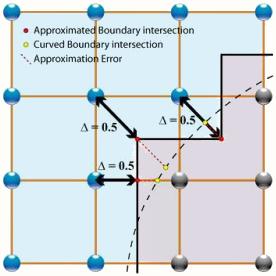
Borde mas general

Primero debe ser definida una frontera aproximada que permita establecer las ecuaciones de borde necesarias. Luego deben ser aplicadas en el proceso de steraming.

ID:(8500, 0)

Descripción

>Top

En el caso de un sistema D2Q9 se tienen los 9 valores f_i que hemos acotado como O, N, E, S, W, NE, SE, SW, NW. Si el numero de partículas en la posición (n,m) se denota como f_i(j.k) se tiene que las ecuaciones son

```

N[x,y] = N[x,y-1]

NW[x,y] = NW[x+1,y-1]

E[x,y] = E[x-1,y]

NE[x,y] = NE[x-1,y-1]

S[x,y] = S[x,y+1]

SE[x,y] = SE[x-1,y+1]

W[x,y] = W[x+1,y]

SW[x,y] = SW[x+1,y+1]

```

ID:(9151, 0)

Ecuación

>Top, >Modelo

En la aproximación de relajación se supone que la distribución f_i(\vec{x},t) tiende a relajarse en un tiempo \tau a una distribución en equilibrio f_i^{eq}(\vec{x},t) según la ecuación\\n\\n

$\displaystyle\frac{df_i}{dt}=-\displaystyle\frac{f_i-f_i^{eq}}{\tau}$

que tiene en la aproximación discreta la ecuación

donde el termino de las diferencias en las funciones distribución representa las colisiones.

ID:(8489, 0)

Descripción

>Top

En el caso D2Q9 el termino colision se calcula sumando los distintos factores

\\n\\npor lo que se tiene para cada celda\\n\\n

$O = O+w(4rho/9)(1-3u2/2) - O)$

\\n

$E = E+w(rho/9)(1+u_x/3+5u_x^2-3u2/2)-E)$

\\n

$W = W+w(rho/9)(1-u_x/3+5u_x^2-3u2/2)-W)$

\\n

$N = N+w(rho/9)(1+u_y/3+5u_y^2-3u2/2)-N)$

\\n

$S = S+w(rho/9)(1-u_y/3+5u_y^2-3u2/2)-S)$

\\n

$NE = NE+w(rho/36)(1+u_x/3+u_y/3+5(u2+2u_xu_y)/2-3u2/2)-NE)$

\\n

$SE = SE+w(rho/36)(1+u_x/3-u_y/3+5(u2-2u_xu_y)/2-3u2/2)-SE)$

\\n

$NW = NW+w(rho/36)(1-u_x/3+u_y/3+5(u2-2u_xu_y)/2-3u2/2)-NW)$

\\n

$SW = SW+w(rho/36)(1-u_x/3-u_y/3+5(u2+2u_xu_y)/2-3u2/2)-SW)$

\\n\\ncon\\n\\n

$u2 = u_x^2+u_y^2$

ID:(9155, 0)

Ecuación

>Top, >Modelo

La distribución en equilibrio se puede aproximar por una distribución de Maxwell Boltzmann

en donde m es la masa de la partícula, T la temperatura del sistema y k la constante de Boltzmann.

ID:(8490, 0)

Ecuación

>Top, >Modelo

En la aproximación Bhatnagar-Gross-Krook la distribución en equilibrio se asume como la de un gas de partículas sin interacción

con \vec{u} la velocidad del flujo, k la constante de Boltzmann, T la temperatura y m la masa de la particula. Si se desarrolla esta expresión en el limite de velocidades \vec{u} comparada con la velocidad de las moleculas c\hat{e}_i se tiene que

con \omega_i los pesos dados por

que se determinan asegurando que la distribución equilibrio cumpla las leyes de conservación.

ID:(9084, 0)

Descripción

>Top

En el caso de partículas de un liquido el método LBM permite desarrollar simuladores como se muestra en el ejemplo:

(html file)

ID:(9156, 0)