Usuario:


Revisión del Método Monte Carlo (MCM)
Storyboard

Aun que el método Monte Carlo (MCM) es visto como la panacea en el calculo de dosis, su aplicación esta limitada por el esfuerzo computacional, Este esta ligada al gran numero de partículas que se deben simular para lograr reducir la incerteza numérica inherente a la complejidad del sistema. En esta revisión se describe el método y se revisa la problemática de la incerteza numérica.

>Modelo

ID:(1161, 0)


Camino aleatorio
Imagen

>Top


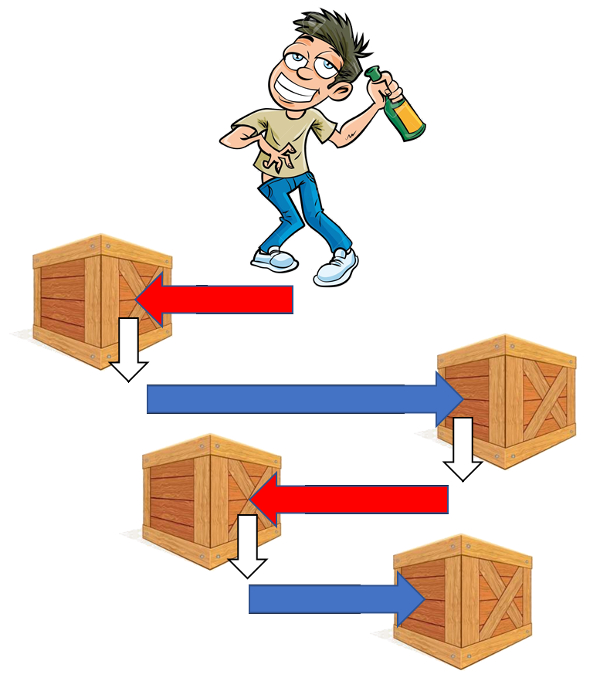
Para explorar las propiedades de Monte Carlo supongamos que queremos simular el comportamiento de un borrachito.

Este se desplaza unidimensionalmente pudiendo dar pasos tanto a la derecha como a la izquierda.

Las distancias recorrida en cada dirección dependen de los objetos en el camino. Estos se encuentran distribuidos en forma aleatoria.

Cada vez que llega a un objeto invierte la dirección en que se desplaza.

ID:(9175, 0)


Distribución de distancias recorridas
Ecuación

>Top, >Modelo


El caso mas simple es el de una particular que se desplaza a lo largo de un eje pudiendo impactar algún objeto.

Si la probabilidad de lograr llegar a una distancia entre x y x+dx es p(x), se tendrá que la probabilidad de impactar será igual a la diferencia de propagación:

p(x)-p(x+dx)\sim-\displaystyle\frac{dp}{dx}dx

Si la probabilidad de llegar a x es p(x) y la probabilidad de impactar en el camino dx es proporcional a dx/\lambda, donde \lambda es un largo característico, se tiene que

dp = -\displaystyle\frac{dx}{\lambda} p(x)

que se puede integrar dando

$p(x)dx = \displaystyle\frac{1}{\lambda}e^{-x/\lambda}dx$

donde \lambda es la constante de integración.

La función p(x) muestra como se distribuyen en la distancia x las ubicaciones en donde ocurre el primer impacto si la partícula inicia su camino en el origen (x=0).

Una distribución de esta forma corresponde a una distribución de Poisson.

ID:(9099, 0)


Simulador camino aleatorio paso variable
Php

>Top


Para obtener la distribución de las partículas en función de la posición se puede realizar una iteración en que

> 0. se define una posición y dirección inicial
> 1. se generado al azar un largo de paso
> 2. se define al azar si se invierte la dirección
> 3. se desplaza según el paso definido en 1 y 2
> 3. se continua en 1

Si se supone que esperamos un tiempo definido y que la partícula se desplaza a velocidad constante, se puede determinar la posición que tiene tras un tiempo dado o tras un camino total definido.

Para comprender como este tipo de simulación depende de los parámetros se propone variar:

> i) la resolución (ancho de la clase con que se estima la distribución)

> ii) numero de iteraciones

ID:(9100, 0)


Conclusiones
Descripción

>Top


Jugando con el simulador notamos que

> 1. Solo tiene sentido considerar distribuciones de posiciones posibles

> 2. La distribución se basa en determinar posiciones en rangos discretos

> 3. Rangos de menor tamaño requieren de un mayor numero de iteraciones

ID:(9101, 0)


Sección eficaz total y camino libre
Ecuación

>Top, >Modelo


La sección efectiva total \sigma está relacionada con la sección efectiva que la partícula ofrece al haz incidente y por lo tanto afecta directamente a la trayectoria libre. Si se multiplica por la concentración de las partículas c se puede demostrar que la trayectoria libre es

ID:(9178, 0)


Compton Scattering
Imagen

>Top


El scattering de Compton ocurre cuando un fotón interactua con una partícula cargada, en particular con un electrón. En el proceso el fotón pierde energía y se desvía poniendo el electrón en movimiento:

ID:(9176, 0)


Scattering de Compton
Ecuación

>Top, >Modelo


El scattering de Compton ocurre cuando un foton interactua con un electrón transfiirendole el primero energía al segundo (interacción inelástica). El largo de onda con que emerge del scatering el foton se puede calcular mediante

$\lambda_2=\lambda+\lambda_c(1-\cos\theta)$



en donde

$\lambda_c=\displaystyle\frac{h}{m_ec}$

es el largo de onda de Compton y \theta el angulo de desvío del foton.

ID:(9145, 0)


Sección eficaz diferencial de scattering de Compton
Ecuación

>Top, >Modelo


En el caso de scattering de Compton, la sección eficaz diferencial es según Klein-Nishina

$\displaystyle\frac{d\sigma_{KN}}{d\Omega}=\displaystyle\frac{3}{16\pi}\displaystyle\frac{\sigma_T}{(1+\epsilon(1-\cos\theta))^2}\left(\epsilon(1-cos\theta)+\displaystyle\frac{1}{1+\epsilon(1-\cos\theta)}-\cos^2\theta\right)$



donde

$\sigma_T=\displaystyle\frac{8\pi}{3}r_0^2$



es la sección eficaz de Thomson y el factor

$\epsilon=\displaystyle\frac{E}{m_ec^2}$

es la energía normalizada.

ID:(9144, 0)


Sección eficaz total de scattering de Compton
Ecuación

>Top, >Modelo


Si se toma la sección eficaz diferencial según Klein-Nishina

$\displaystyle\frac{d\sigma_{KN}}{d\Omega}=\displaystyle\frac{3}{16\pi}\displaystyle\frac{\sigma_T}{(1+\epsilon(1-\cos\theta))^2}\left(\epsilon(1-cos\theta)+\displaystyle\frac{1}{1+\epsilon(1-\cos\theta)}-\cos^2\theta\right)$



y se integra en el angulo solido

$d\Omega=2\pi \sin\theta d\theta$



se obtiene la sección eficaz total

$\sigma_{KN}=\displaystyle\frac{3}{4}\sigma_T\left(\displaystyle\frac{(1+\epsilon)}{\epsilon^3}\left(\displaystyle\frac{2\epsilon(1+\epsilon)}{1+2\epsilon}-\log(1+2\epsilon)\right)+\displaystyle\frac{\log(1+2\epsilon)}{2\epsilon}-\displaystyle\frac{(1+3\epsilon)}{(1+2\epsilon)^2}\right)$



donde

$\sigma_T=\displaystyle\frac{8\pi}{3}r_0^2$



es la sección eficaz de Thomson y el factor

$\epsilon=\displaystyle\frac{E}{m_ec^2}$

es la energía normalizada.

En el limite de pequeños \epsilon\ll 1 se tiene que la sección total es

\sigma_{KN}\sim\sigma_T\left(1-2\epsilon+\displaystyle\frac{26}{5}\epsilon^2\ldots\right)

y en el limite \epsilon\gg 1 se tiene que la sección total es

\sigma_{KN}\sim\displaystyle\frac{3}{8}\displaystyle\frac{\sigma_T}{\epsilon}\left(\log(2\epsilon)+\displaystyle\frac{1}{2}\right)

ID:(9111, 0)


Simulador camino aleatorio con scattering de Compton
Php

>Top


Se puede estudiar el modelo de Klein-Nishina en forma numérica. Para ello se muestra

- la sección eficaz total en función de la energía del foton
- la sección diferencial en función del angulo para las energías mínima, media y máxima que se definan
- lo que seria la sección eficaz total en un sistema unidimensional que da según la energía transmisión o reflexión

ID:(9114, 0)