Análisis de la fracción de tejido y su dosis
Definición 
Análisis de la fracción de tejido y su dosis
ID:(2714, 0)
Factor DVH
Nota 
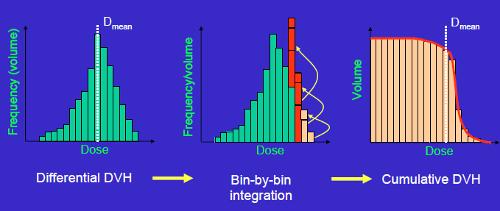
Para poder estimar que tan bueno es un plan cuando la información es 3D se puede proceder a sumar todos los voxeles que tienen la misma dosis y así generar un diagrama unidimensional:
ID:(1501, 0)
Probabilidad de complicaciones en tejido normal (NTCP)
Ejercicio 
El segundo aspecto claves dentro del desarrollo del tratamiento optimo es minimizar la probabilidad de efectos adversos por el tratamiento, lo que en ingles se denomina el normal tissue complication probability, NTCP. Existen varios modelos que permiten estimar dicha probabilidad.
ID:(1499, 0)
Comparación TCP y NTCP
Ecuación 
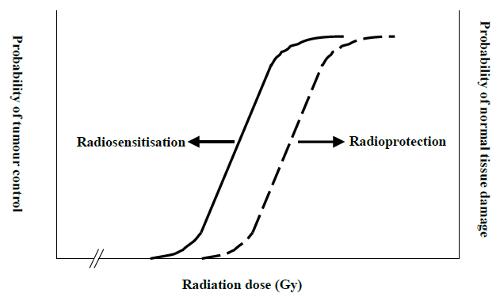
La siguiente gráfica muestra la distribución probabilística de daño a órganos (linea azul) que da origen a la función de probabilidad de complicaciones en tejido normal (NTCP) (linea amarilla):

Adicionalmente se incluye la curva probabilidad de control de tumor TCP para compararla con la de TCP (linea roja).
El objetivo debe ser:
- lograr evitar irradiar órganos sensibles de modo de que la distribución de probable secuela sea mínima (linea azul) y con ello el NTCP (linea amarilla) sea lo mas plana posible solo aumentando para dosis mayores que la que se usara
- lograr que la linea de control de tumor TCP (linea roja) llegue a los mayores valores posibles a baja dosis asegurando asi el control del tumor
ID:(2713, 0)
Probabilidad de Complicaciones en Tejido Normal (NTCP)
Storyboard 
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
En el caso de haber solo un voxel, la dosis efectiva es igual a la dosis del voxel
dato que la fracci n de volumen es la unidad.
En el caso de haber mas de un rgano que puede afectar el tratamiento, se debe calcular el NTCP para cada uno de estos y calcular el NTCP total
donde se supone que la probabilidad de no haber problemas
En caso de existir dos rganos con respectivos
An lisis de la fracci n de tejido y su dosis
Modelo de Lyman-Kutcher-Burman (NTCP)
La integral de la gausseana se puede representar con una desviaci n m xima del
La estimaci n de la probabilidad de complicaciones en el Modelo Lyman Kutcher Burman (LKB) asumiendo que la probabilidad de falle se puede representar como una gauseana en torno a la dosis $D_{50}$. Por ello el valor del NTCP se estima integrando la gauseana hasta el valor de $t$:
La probabilidad de falla de un organo se estima en base a la desviaci n de la dosis efectiva calculada para el tejido sano
El factor
Para poder estimar que tan bueno es un plan cuando la informaci n es 3D se puede proceder a sumar todos los voxeles que tienen la misma dosis y as generar un diagrama unidimensional:
La integral de la gauseana se puede aproximar por la expresi n
por lo que se tiene que en primera aproximaci n el NTCP es:
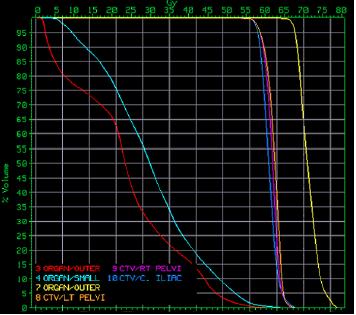
Calculo del DVH
La dosis se calcula considerando la fracci n de los volumenes $v_i$ de los distintos elementos $i$ en que se subdivide el cuerpo del paciente (voxels).
Con ello la dosis efectiva es:
donde $n$ es un factor que se ajusta y su valor esta en torno de la unidad.
El segundo aspecto claves dentro del desarrollo del tratamiento optimo es minimizar la probabilidad de efectos adversos por el tratamiento, lo que en ingles se denomina el normal tissue complication probability, NTCP. Existen varios modelos que permiten estimar dicha probabilidad.
La siguiente gr fica muestra la distribuci n probabil stica de da o a rganos (linea azul) que da origen a la funci n de probabilidad de complicaciones en tejido normal (NTCP) (linea amarilla):
Adicionalmente se incluye la curva probabilidad de control de tumor TCP para compararla con la de TCP (linea roja).
El objetivo debe ser:
- lograr evitar irradiar rganos sensibles de modo de que la distribuci n de probable secuela sea m nima (linea azul) y con ello el NTCP (linea amarilla) sea lo mas plana posible solo aumentando para dosis mayores que la que se usara
- lograr que la linea de control de tumor TCP (linea roja) llegue a los mayores valores posibles a baja dosis asegurando asi el control del tumor
La dosis se calcula considerando la fracci n de los volumenes $v_i$ de los distintos elementos $i$ en que se subdivide el cuerpo del paciente (voxels).
Con ello la dosis efectiva es:
donde $n$ es un factor que se ajusta y su valor esta en torno de la unidad.
La dosis se calcula considerando la fracci n de los volumenes $v_i$ de los distintos elementos $i$ en que se subdivide el cuerpo del paciente (voxels).
Con ello la dosis efectiva es:
donde $n$ es un factor que se ajusta y su valor esta en torno de la unidad.
La dosis se calcula considerando la fracci n de los volumenes $v_i$ de los distintos elementos $i$ en que se subdivide el cuerpo del paciente (voxels).
Con ello la dosis efectiva es:
donde $n$ es un factor que se ajusta y su valor esta en torno de la unidad.
La dosis se calcula considerando la fracci n de los volumenes $v_i$ de los distintos elementos $i$ en que se subdivide el cuerpo del paciente (voxels).
Con ello la dosis efectiva es:
donde $n$ es un factor que se ajusta y su valor esta en torno de la unidad.
Probabilidad de complicaciones seg n el modelo de Zaider-Amols:
ID:(741, 0)