Usuario:
Oscilador armónico
Storyboard 
Mediante el oscilador armónico, podemos analizar la probabilidad de que una partícula se encuentre en una posición o velocidad específica dentro de un rango determinado. Esto nos permite comprender cómo se utiliza el espacio de fase tanto en términos de momento como de posición.
ID:(1558, 0)
Modelo de oscilador armónico
Definición
Un oscilador armónico es un sistema que esta expuesto a una fuerza proporcional a la distancia al punto de equilibrio que siempre de opone al alejarse de este. Un ejemplo de oscilador armónico lo representa una masa fijada a dos resortes:
ID:(11462, 0)
Curva de en el espacio de fase del oscilador armónico
Imagen
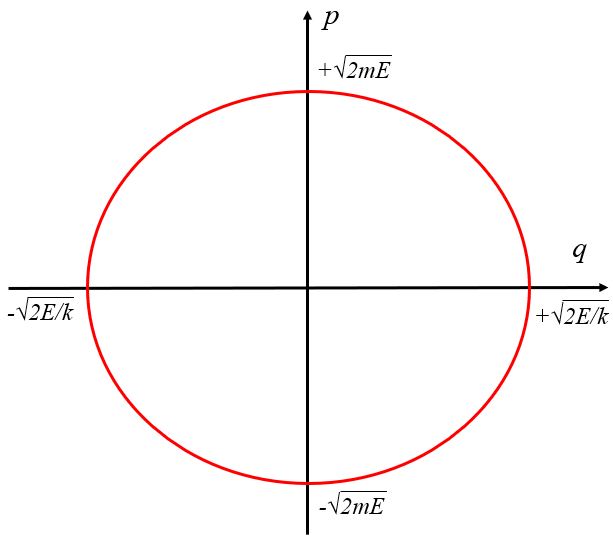
La energía de un oscilador armónico con es
| $ \displaystyle\frac{ p ^2}{ 2 m E }+\displaystyle\frac{ q ^2}{ 2 E / k }=1 $ |
lo que se representa como la elipse que muestra la gráfica:
ID:(11467, 0)
Rango en curva de en el espacio de fase del oscilador armónico
Nota
La probabilidad solo tiene sentido en la medida que se refiere a un rango ya que de lo contrario sería nula. En el caso del oscilador armónico el rango en que buscamos estudiar es el de la energía, es decir la energía del sistema esta entre
ID:(11468, 0)
Probabilidad de encontrar el oscilador armónico en una posición
Cita
La probabilidad de encontrar la partícula en una posición entre
ID:(11469, 0)
Probabilidad de encontrar el oscilador armónico con un momento
Ejercicio
La probabilidad de encontrar la partícula con una memento entre
ID:(11470, 0)
Oscilador armónico
Storyboard
Mediante el oscilador armónico, podemos analizar la probabilidad de que una partícula se encuentre en una posición o velocidad específica dentro de un rango determinado. Esto nos permite comprender cómo se utiliza el espacio de fase tanto en términos de momento como de posición.
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Ejemplos
Un oscilador arm nico es un sistema que esta expuesto a una fuerza proporcional a la distancia al punto de equilibrio que siempre de opone al alejarse de este. Un ejemplo de oscilador arm nico lo representa una masa fijada a dos resortes:
En el caso cl sico de una part cula de masa
La ecuaci n de la energ a del oscilador arm nico con
se puede reescribir en la forma t pica de una ecuaci n de una elipse con
con los ejes mayor
y el eje menor
El eje mayor de la elipse del oscilador arm nico en el espacio de fase es con
es con
El eje menor de la elipse del oscilador arm nico en el espacio de fase es con
es igual con
La energ a de un oscilador arm nico con
lo que se representa como la elipse que muestra la gr fica:
La probabilidad solo tiene sentido en la medida que se refiere a un rango ya que de lo contrario ser a nula. En el caso del oscilador arm nico el rango en que buscamos estudiar es el de la energ a, es decir la energ a del sistema esta entre
rea de una elipse
El rea de una elipse con
cuyo eje mayor es
y cuyo eje menor es
se calcula con
Usando el rea delipse en el espacio de fase del oscilador arm nico con
el rea en el espacio de fase se obtiene restando el rea en la energ a $E+dE$ al rea en la energ a $E$:
$2 \pi (E + dE)\sqrt{\displaystyle\frac{m}{k}} - 2 \pi E \sqrt{\displaystyle\frac{m}{k}} = 2 \pi E \sqrt{\displaystyle\frac{m}{k}}$
En otras palabras, con
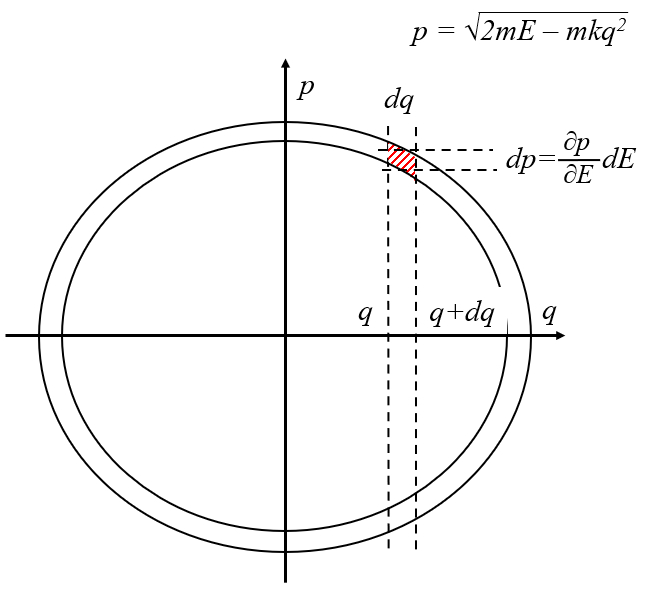
La probabilidad de encontrar la part cula en una posici n entre
Con el rea de la capa con
y la ecuaci n de la elipse con
$dp =\displaystyle\frac{\partial}{\partial E}\sqrt{2 m E - k m q^2} dE =\displaystyle\frac{m}{\sqrt{2 m E - m k q ^2}} dE $
con lo que la probabilidad es con
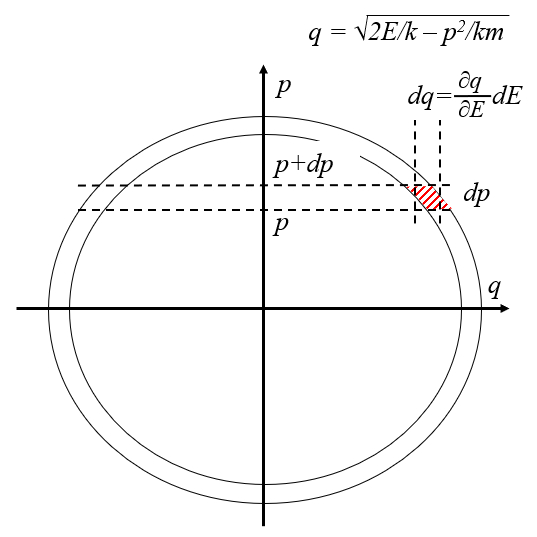
La probabilidad de encontrar la part cula con una memento entre
Con el rea de la capa con
y la ecuaci n de la elipse con
$dq =\displaystyle\frac{\partial}{\partial E}\sqrt{2 E / k - p ^2/ m k } dE=\displaystyle\frac{ m }{\sqrt{2 m E - m k q ^2}} dE$
con lo que la probabilidad es con
ID:(1558, 0)