Benützer:


Harmonischer Oszillator
Storyboard

Mithilfe des harmonischen Oszillators können wir die Wahrscheinlichkeit untersuchen, eine Teilchen an einer bestimmten Position oder Geschwindigkeit innerhalb eines definierten Bereichs zu finden. Dies ermöglicht uns zu verstehen, wie der Phasenraum sowohl in Bezug auf den Impuls als auch die Position genutzt wird.

>Modell

ID:(1558, 0)


Harmonisches Oszillatormodell
Definition

Ein harmonischer Oszillator ist ein System, das einer Kraft ausgesetzt ist, die proportional zum Abstand zum Gleichgewichtspunkt ist, dem es immer entgegenwirkt, wenn es sich von ihm entfernt. Ein Beispiel für einen harmonischen Oszillator ist eine Masse, die an zwei Federn befestigt ist:

ID:(11462, 0)


Phasenraumkurve des harmonischen Oszillators
Bild

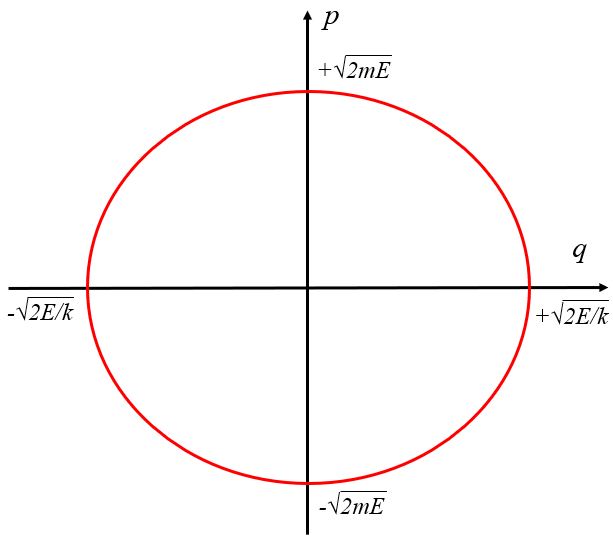
La energía de un oscilador armónico con constante del resorte $N/m$, entropia del sistema $J/K$, masa de la partícula $kg$, momento de la partícula $kg m/s$ und posición $m$ es

$ \displaystyle\frac{ p ^2}{ 2 m E }+\displaystyle\frac{ q ^2}{ 2 E / k }=1 $



lo que se representa como la elipse que muestra la gráfica:

ID:(11467, 0)


Gekrümmter Bereich des Phasenraums des harmonischen Oszillators
Notiz

Wahrscheinlichkeit ist nur insoweit sinnvoll, als sie sich auf einen Bereich bezieht, da sie sonst null wäre. Im Fall des harmonischen Oszillators ist der Bereich, in dem wir untersuchen möchten, der der Energie, dh die Energie des Systems liegt zwischen E und E+dE. Wenn es im Phasenraum dargestellt wird, gibt es einen Bereich:

ID:(11468, 0)


Wahrscheinlichkeit, den harmonischen Oszillator in einer Position zu finden
Zitat

Die Wahrscheinlichkeit, das Teilchen an einer Position zwischen q und q+dq zu finden, entspricht der Schätzung der Zustände in diesem Bereich in Bezug auf alle Zustände, für die die Energie ist zwischen E und E+dE:

ID:(11469, 0)


Wahrscheinlichkeit, den harmonischen Oszillator mit einem Moment zu finden
Übung

Die Wahrscheinlichkeit, das Teilchen mit einem Andenken zwischen p und p+dp zu finden, entspricht der Schätzung der Zustände in diesem Bereich in Bezug auf alle Zustände, für die die Energie ist zwischen E und E+dE:

ID:(11470, 0)


Harmonischer Oszillator
Beschreibung

Mithilfe des harmonischen Oszillators können wir die Wahrscheinlichkeit untersuchen, eine Teilchen an einer bestimmten Position oder Geschwindigkeit innerhalb eines definierten Bereichs zu finden. Dies ermöglicht uns zu verstehen, wie der Phasenraum sowohl in Bezug auf den Impuls als auch die Position genutzt wird.

Variablen
Symbol
Text
Variable
Wert
Einheiten
Berechnen
MKS-Wert
MKS-Einheiten
$S$
S
Acción
J s
$k$
k
Constante del resorte
N/m
$p(p)$
p_p
Densidad de probabilidad de un momento
-
$p(q)$
p_q
Densidad de probabilidad de un posición
-
$a$
a
Eje mayor de la elipse
m
$b$
b
Eje menor de la elipse
kg m/s
$dE$
dE
Elemento de energía
J
$dS$
dS
Elemento de superficie de acción
J s
$E$
E
Energía del sistema
J
$S$
S
Entropia del sistema
J/K
$r$
r
Krümmung Radio
m
$m$
m
Masa de la partícula
kg
$p$
p
Momento de la partícula
kg m/s
$S$
S
Oberfläche der Luftblase
m^2
$\vec{q}$
&q
Posición
m
$dp$
dp
Rango de momento
kg m/s
$dq$
dq
Rango de posición
m

Berechnungen

Zuerst die Gleichung auswählen:   zu ,  dann die Variable auswählen:   zu 
Symbol
Gleichung
Gelöst
Übersetzt

Berechnungen

Symbol
Gleichung
Gelöst
Übersetzt

 Variable   Gegeben   Berechnen   Ziel :   Gleichung   Zu verwenden


Gleichungen

Beispiele

Ein harmonischer Oszillator ist ein System, das einer Kraft ausgesetzt ist, die proportional zum Abstand zum Gleichgewichtspunkt ist, dem es immer entgegenwirkt, wenn es sich von ihm entfernt. Ein Beispiel f r einen harmonischen Oszillator ist eine Masse, die an zwei Federn befestigt ist:

(ID 11462)

En el caso cl sico de una part cula de masa m en un potencial arm nico con constante k el sistema puede aceder a cualquier estado (q,p) mientras su energ a sea con

$E=\displaystyle\frac{p^2}{2m}+\displaystyle\frac{1}{2}kq^2$

(ID 3421)

La ecuaci n de la energ a del oscilador arm nico con constante del resorte $N/m$, energía del sistema $J$, masa de la partícula $kg$, momento de la partícula $kg m/s$ und posición $m$

$E=\displaystyle\frac{p^2}{2m}+\displaystyle\frac{1}{2}kq^2$



se puede reescribir en la forma t pica de una ecuaci n de una elipse con constante del resorte $N/m$, energía del sistema $J$, masa de la partícula $kg$, momento de la partícula $kg m/s$ und posición $m$

$ \displaystyle\frac{ p ^2}{ 2 m E }+\displaystyle\frac{ q ^2}{ 2 E / k }=1 $

(ID 11477)

El eje mayor de la elipse del oscilador arm nico en el espacio de fase es con constante del resorte $N/m$, entropia del sistema $J/K$, masa de la partícula $kg$, momento de la partícula $kg m/s$ und posición $m$

$ \displaystyle\frac{ p ^2}{ 2 m E }+\displaystyle\frac{ q ^2}{ 2 E / k }=1 $



es con constante del resorte $N/m$, entropia del sistema $J/K$, masa de la partícula $kg$, momento de la partícula $kg m/s$ und posición $m$ igual a

$ a ^2 =\displaystyle\frac{ 2 E }{ k }$

(ID 11478)

El eje menor de la elipse del oscilador arm nico en el espacio de fase es con constante del resorte $N/m$, entropia del sistema $J/K$, masa de la partícula $kg$, momento de la partícula $kg m/s$ und posición $m$

$ \displaystyle\frac{ p ^2}{ 2 m E }+\displaystyle\frac{ q ^2}{ 2 E / k }=1 $



es igual con constante del resorte $N/m$, entropia del sistema $J/K$, masa de la partícula $kg$, momento de la partícula $kg m/s$ und posición $m$ a

$ b ^2 =2 m E $

(ID 11479)

La energ a de un oscilador arm nico con constante del resorte $N/m$, entropia del sistema $J/K$, masa de la partícula $kg$, momento de la partícula $kg m/s$ und posición $m$ es

$ \displaystyle\frac{ p ^2}{ 2 m E }+\displaystyle\frac{ q ^2}{ 2 E / k }=1 $



lo que se representa como la elipse que muestra la gr fica:

(ID 11467)

Wahrscheinlichkeit ist nur insoweit sinnvoll, als sie sich auf einen Bereich bezieht, da sie sonst null w re. Im Fall des harmonischen Oszillators ist der Bereich, in dem wir untersuchen m chten, der der Energie, dh die Energie des Systems liegt zwischen E und E+dE. Wenn es im Phasenraum dargestellt wird, gibt es einen Bereich:

(ID 11468)

Bereich einer Ellipse

$ S = \pi a b $

(ID 4446)

Die Fl che einer Ellipse mit krümmung Radio $m$ und oberfläche der Luftblase $m^2$

$ S = \pi a b $



deren Hauptachse constante del resorte $N/m$, eje mayor de la elipse $m$ und energía del sistema $J$

$ a ^2 =\displaystyle\frac{ 2 E }{ k }$



und deren Nebenachse eje menor de la elipse $kg m/s$, energía del sistema $J$ und masa de la partícula $kg$

$ b ^2 =2 m E $



wird mithilfe einer eje menor de la elipse $kg m/s$, energía del sistema $J$ und masa de la partícula $kg$

$ S = 2 \pi E \sqrt{\displaystyle\frac{ m }{ k }}$

berechnet.

(ID 11480)

Mit der Fl che der Phasenraumellipse des harmonischen Oszillators mit acción $J s$, constante del resorte $N/m$, energía del sistema $J$ und masa de la partícula $kg$

$ S = 2 \pi E \sqrt{\displaystyle\frac{ m }{ k }}$



wird die Phasenraumfl che erhalten, indem man die Fl che bei der Energie $E+dE$ von der Fl che bei der Energie $E$ subtrahiert:

$2 \pi (E + dE)\sqrt{\displaystyle\frac{m}{k}} - 2 \pi E \sqrt{\displaystyle\frac{m}{k}} = 2 \pi E \sqrt{\displaystyle\frac{m}{k}}$



Also, mit acción $J s$, constante del resorte $N/m$, energía del sistema $J$ und masa de la partícula $kg$:

$ dS = 2 \pi \sqrt{\displaystyle\frac{ m }{ k }} dE $

(ID 11482)

Die Wahrscheinlichkeit, das Teilchen an einer Position zwischen q und q+dq zu finden, entspricht der Sch tzung der Zust nde in diesem Bereich in Bezug auf alle Zust nde, f r die die Energie ist zwischen E und E+dE:

(ID 11469)

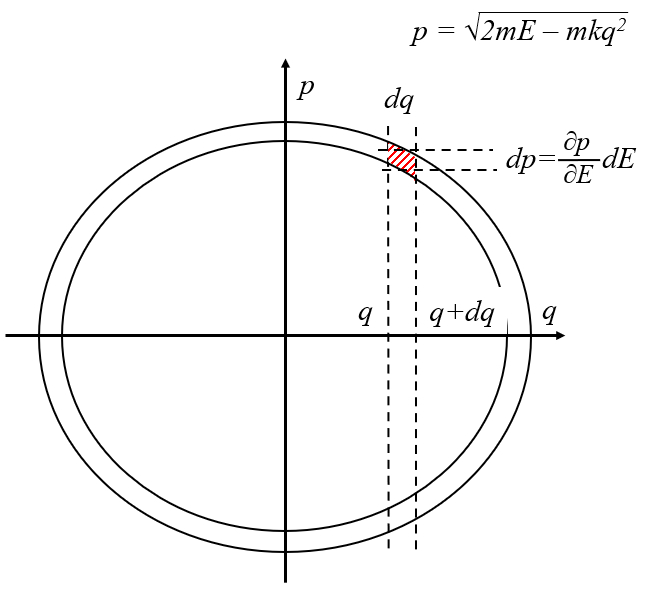
Con el rea de la capa con constante del resorte $N/m$, elemento de energía $J$, elemento de superficie de acción $J s$ und masa de la partícula $kg$

$ dS = 2 \pi \sqrt{\displaystyle\frac{ m }{ k }} dE $



y la ecuaci n de la elipse con constante del resorte $N/m$, entropia del sistema $J/K$, masa de la partícula $kg$, momento de la partícula $kg m/s$ und posición $m$

$ \displaystyle\frac{ p ^2}{ 2 m E }+\displaystyle\frac{ q ^2}{ 2 E / k }=1 $

\\n\\nse puede calcular la altura del segmento dq\\n\\n

$dp =\displaystyle\frac{\partial}{\partial E}\sqrt{2 m E - k m q^2} dE =\displaystyle\frac{m}{\sqrt{2 m E - m k q ^2}} dE $



con lo que la probabilidad es con constante del resorte $N/m$, entropia del sistema $J/K$, masa de la partícula $kg$, momento de la partícula $kg m/s$ und posición $m$

$ P(q) dq = \displaystyle\frac{ dq }{\sqrt{\displaystyle\frac{2 E }{ k }- q ^2}}$

(ID 11481)

Die Wahrscheinlichkeit, das Teilchen mit einem Andenken zwischen p und p+dp zu finden, entspricht der Sch tzung der Zust nde in diesem Bereich in Bezug auf alle Zust nde, f r die die Energie ist zwischen E und E+dE:

(ID 11470)

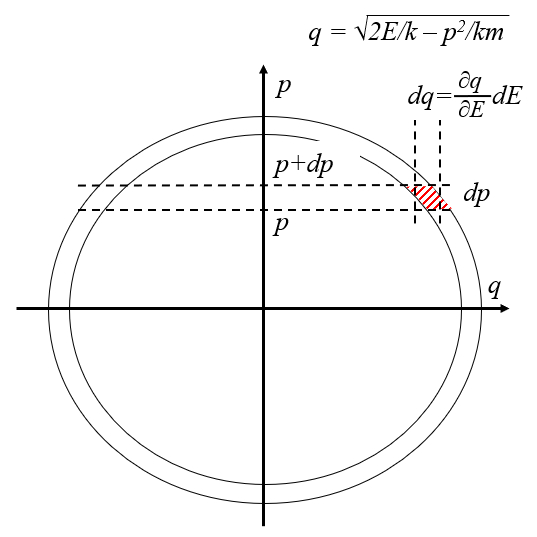
Con el rea de la capa con constante del resorte $N/m$, elemento de energía $J$, elemento de superficie de acción $J s$ und masa de la partícula $kg$

$ dS = 2 \pi \sqrt{\displaystyle\frac{ m }{ k }} dE $



y la ecuaci n de la elipse con constante del resorte $N/m$, entropia del sistema $J/K$, masa de la partícula $kg$, momento de la partícula $kg m/s$ und posición $m$

$ \displaystyle\frac{ p ^2}{ 2 m E }+\displaystyle\frac{ q ^2}{ 2 E / k }=1 $

\\n\\nse puede calcular la altura del segmento dq\\n\\n

$dq =\displaystyle\frac{\partial}{\partial E}\sqrt{2 E / k - p ^2/ m k } dE=\displaystyle\frac{ m }{\sqrt{2 m E - m k q ^2}} dE$



con lo que la probabilidad es con constante del resorte $N/m$, entropia del sistema $J/K$, masa de la partícula $kg$, momento de la partícula $kg m/s$ und posición $m$

$ P(p) dp = \displaystyle\frac{ dp }{\sqrt{2 m E - p ^2}}$

(ID 11483)

ID:(1558, 0)