Usuario:
Sistema de partículas en 1D
Storyboard 
Consideremos varias partículas en una dimensión que no interactúan entre sí y discutamos cómo obtener la probabilidad de que una de ellas tenga un momento dentro de un rango específico.
ID:(1559, 0)
Dos partículas en una caja
Definición
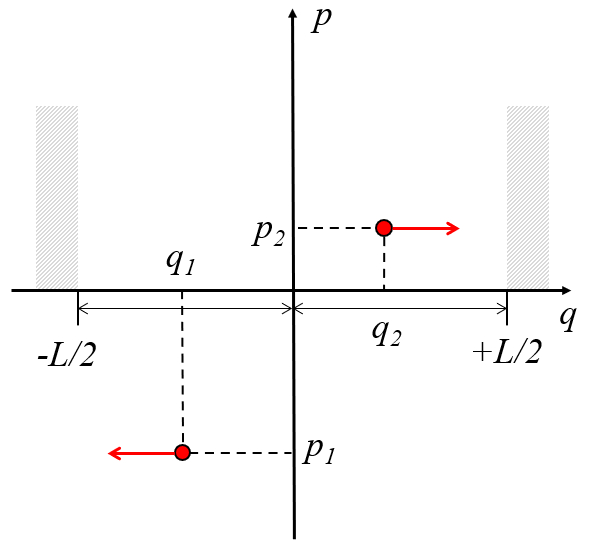
Dos partículas en una caja rebotando en las paredes a una distancia
ID:(11471, 0)
Espacio de fase de las dos partículas
Imagen
Si se consideran dos partículas con una energía total en un rango entre
| $ E = \displaystyle\frac{ p_1 ^2}{2 m }+ \displaystyle\frac{ p_2 ^2}{2 m }$ |
lo que se representa a continuación con :
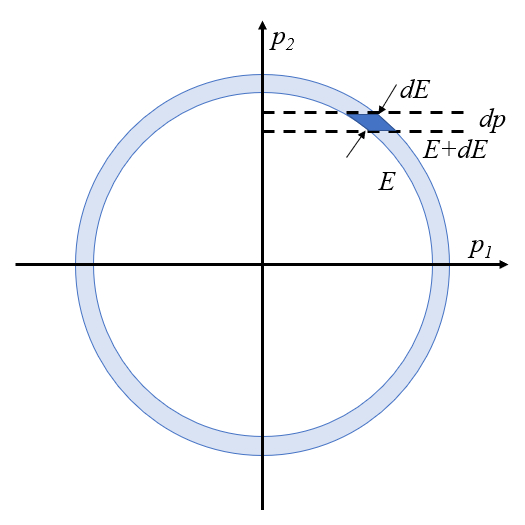
En este caso:
• existen dos grados de libertad, uno por cada partícula
• existe una restricción, que es el rango en que esta la energía del sistema
• el calculo de la probabilidad de encontrar el momento en un rango represente la segunda restricción
Por ello el calculo de la probabilidad es una solución directa de las ecuaciones del sistema sin que existan grados de libertad adicionales.
ID:(11472, 0)
Espacio de fase de las tres partículas
Nota
Si se consideran tres partículas con una energía total en un rango entre
| $ E = \displaystyle\frac{ p_1 ^2}{2 m }+ \displaystyle\frac{ p_2 ^2}{2 m }+ \displaystyle\frac{ p_3 ^2}{2 m }$ |
lo que se representa a continuación:
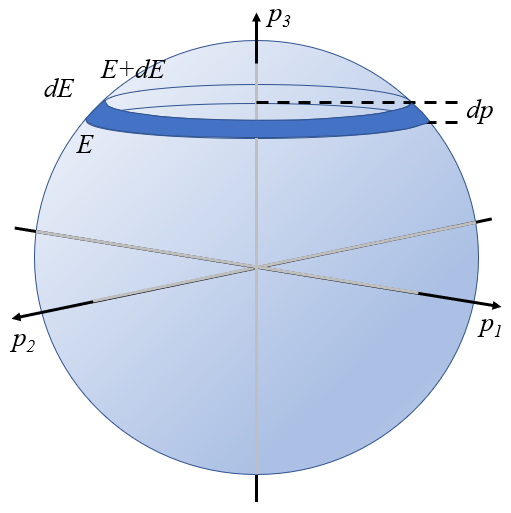
En este caso:
• existen tres grados de libertad, uno por cada partícula
• existe una restricción, que es el rango en que esta la energía del sistema
• el calculo de la probabilidad de encontrar el momento en un rango represente la segunda restricción
Por ello el sistema tiene un grado de libertad que no es determinado por las restricciones. Esto significa que, al ser todos los estados son igualmente probables, debe sumarse (integrarse) sobre todos los valores que puede tomar el grado de libertad.
En un sistema de mayor numero de grados de libertad debe siempre sumarse (integrarse) sobre todos los grados de libertad que no están restringidos.
ID:(11502, 0)
Sistema de partículas en 1D
Descripción
Consideremos varias partículas en una dimensión que no interactúan entre sí y discutamos cómo obtener la probabilidad de que una de ellas tenga un momento dentro de un rango específico.
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Ejemplos
Dos part culas en una caja rebotando en las paredes a una distancia
(ID 11471)
Si las part culas son libres su energ a sera con solo cin tica por lo que
| $ E = \displaystyle\frac{ p_1 ^2}{2 m }+ \displaystyle\frac{ p_2 ^2}{2 m }$ |
(ID 11484)
Si se consideran dos part culas con una energ a total en un rango entre
| $ E = \displaystyle\frac{ p_1 ^2}{2 m }+ \displaystyle\frac{ p_2 ^2}{2 m }$ |
lo que se representa a continuaci n con :
En este caso:
• existen dos grados de libertad, uno por cada part cula
• existe una restricci n, que es el rango en que esta la energ a del sistema
• el calculo de la probabilidad de encontrar el momento en un rango represente la segunda restricci n
Por ello el calculo de la probabilidad es una soluci n directa de las ecuaciones del sistema sin que existan grados de libertad adicionales.
(ID 11472)
Si las part culas son libres su energ a sera con solo cin tica por lo que
| $ E = \displaystyle\frac{ p_1 ^2}{2 m }+ \displaystyle\frac{ p_2 ^2}{2 m }+ \displaystyle\frac{ p_3 ^2}{2 m }$ |
(ID 11501)
Si se consideran tres part culas con una energ a total en un rango entre
| $ E = \displaystyle\frac{ p_1 ^2}{2 m }+ \displaystyle\frac{ p_2 ^2}{2 m }+ \displaystyle\frac{ p_3 ^2}{2 m }$ |
lo que se representa a continuaci n:
En este caso:
• existen tres grados de libertad, uno por cada part cula
• existe una restricci n, que es el rango en que esta la energ a del sistema
• el calculo de la probabilidad de encontrar el momento en un rango represente la segunda restricci n
Por ello el sistema tiene un grado de libertad que no es determinado por las restricciones. Esto significa que, al ser todos los estados son igualmente probables, debe sumarse (integrarse) sobre todos los valores que puede tomar el grado de libertad.
En un sistema de mayor numero de grados de libertad debe siempre sumarse (integrarse) sobre todos los grados de libertad que no est n restringidos.
(ID 11502)
ID:(1559, 0)