Benützer:
1D Partikelsystem
Storyboard 
Betrachten wir mehrere nicht miteinander interagierende Teilchen in einer Dimension und diskutieren, wie wir die Wahrscheinlichkeit berechnen können, dass eines von ihnen einen Impuls innerhalb eines bestimmten Bereichs hat.
ID:(1559, 0)
Zwei Partikel in einer Box
Definition
Zwei Teilchen in einer Box, die in einem Abstand von
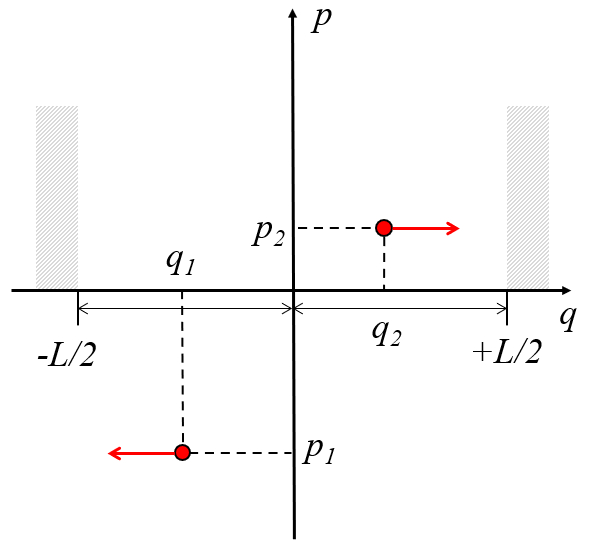
ID:(11471, 0)
Phasenraum der beiden Teilchen
Bild
Si se consideran dos partículas con una energía total en un rango entre
| $ E = \displaystyle\frac{ p_1 ^2}{2 m }+ \displaystyle\frac{ p_2 ^2}{2 m }$ |
lo que se representa a continuación con :
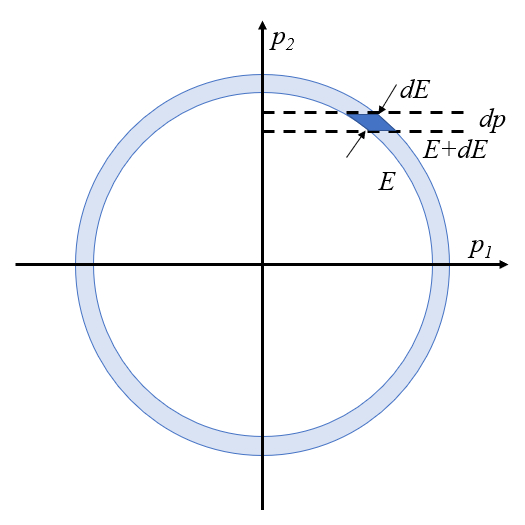
En este caso:
• existen dos grados de libertad, uno por cada partícula
• existe una restricción, que es el rango en que esta la energía del sistema
• el calculo de la probabilidad de encontrar el momento en un rango represente la segunda restricción
Por ello el calculo de la probabilidad es una solución directa de las ecuaciones del sistema sin que existan grados de libertad adicionales.
ID:(11472, 0)
Phasenraum der drei Teilchen
Notiz
Si se consideran tres partículas con una energía total en un rango entre
| $ E = \displaystyle\frac{ p_1 ^2}{2 m }+ \displaystyle\frac{ p_2 ^2}{2 m }+ \displaystyle\frac{ p_3 ^2}{2 m }$ |
lo que se representa a continuación:
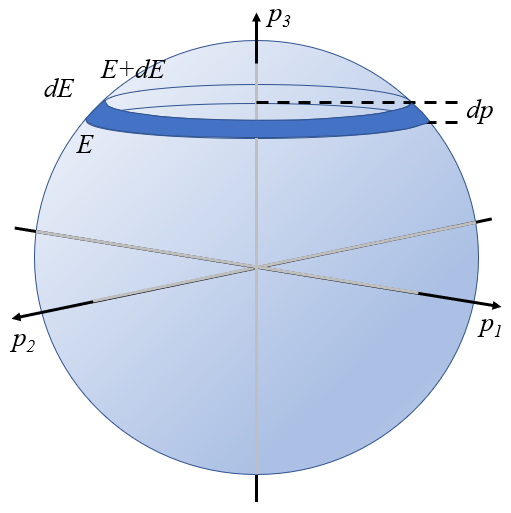
En este caso:
• existen tres grados de libertad, uno por cada partícula
• existe una restricción, que es el rango en que esta la energía del sistema
• el calculo de la probabilidad de encontrar el momento en un rango represente la segunda restricción
Por ello el sistema tiene un grado de libertad que no es determinado por las restricciones. Esto significa que, al ser todos los estados son igualmente probables, debe sumarse (integrarse) sobre todos los valores que puede tomar el grado de libertad.
En un sistema de mayor numero de grados de libertad debe siempre sumarse (integrarse) sobre todos los grados de libertad que no están restringidos.
ID:(11502, 0)
1D Partikelsystem
Beschreibung
Betrachten wir mehrere nicht miteinander interagierende Teilchen in einer Dimension und diskutieren, wie wir die Wahrscheinlichkeit berechnen können, dass eines von ihnen einen Impuls innerhalb eines bestimmten Bereichs hat.
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
Beispiele
Zwei Teilchen in einer Box, die in einem Abstand von
(ID 11471)
Si las part culas son libres su energ a sera con solo cin tica por lo que
| $ E = \displaystyle\frac{ p_1 ^2}{2 m }+ \displaystyle\frac{ p_2 ^2}{2 m }$ |
(ID 11484)
Si se consideran dos part culas con una energ a total en un rango entre
| $ E = \displaystyle\frac{ p_1 ^2}{2 m }+ \displaystyle\frac{ p_2 ^2}{2 m }$ |
lo que se representa a continuaci n con :
En este caso:
• existen dos grados de libertad, uno por cada part cula
• existe una restricci n, que es el rango en que esta la energ a del sistema
• el calculo de la probabilidad de encontrar el momento en un rango represente la segunda restricci n
Por ello el calculo de la probabilidad es una soluci n directa de las ecuaciones del sistema sin que existan grados de libertad adicionales.
(ID 11472)
Si las part culas son libres su energ a sera con solo cin tica por lo que
| $ E = \displaystyle\frac{ p_1 ^2}{2 m }+ \displaystyle\frac{ p_2 ^2}{2 m }+ \displaystyle\frac{ p_3 ^2}{2 m }$ |
(ID 11501)
Si se consideran tres part culas con una energ a total en un rango entre
| $ E = \displaystyle\frac{ p_1 ^2}{2 m }+ \displaystyle\frac{ p_2 ^2}{2 m }+ \displaystyle\frac{ p_3 ^2}{2 m }$ |
lo que se representa a continuaci n:
En este caso:
• existen tres grados de libertad, uno por cada part cula
• existe una restricci n, que es el rango en que esta la energ a del sistema
• el calculo de la probabilidad de encontrar el momento en un rango represente la segunda restricci n
Por ello el sistema tiene un grado de libertad que no es determinado por las restricciones. Esto significa que, al ser todos los estados son igualmente probables, debe sumarse (integrarse) sobre todos los valores que puede tomar el grado de libertad.
En un sistema de mayor numero de grados de libertad debe siempre sumarse (integrarse) sobre todos los grados de libertad que no est n restringidos.
(ID 11502)
ID:(1559, 0)