User:
Pressure difference
Storyboard 
When two columns of liquid with different heights are connected, it can generate a pressure difference that leads to a flow of liquid from the taller column to the shorter one. This movement continues until both columns reach the same height, eliminating any pressure difference.
ID:(1608, 0)
Connecting two liquid columns
Concept
If two columns of water with different heights at their bases are connected, a situation arises where there is a pressure difference along the connecting tube.
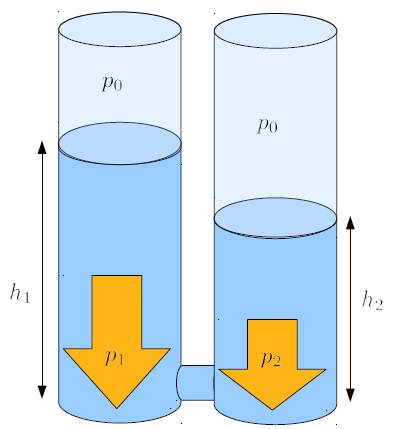
This setup allows us to study how the pressure difference generates a liquid flow along the tube. We can consider an element of liquid with a certain length and a section equal to that of the tube, and estimate the corresponding mass using the density. With the section, we can also convert the pressure difference into a force difference and, ultimately, study how volumes in liquids are accelerated due to pressure differences.
ID:(933, 0)
Pressure difference between columns
Concept
If there is the pressure difference ($\Delta p$) between two points, as determined by the equation:
| $ dp = p - p_0 $ |
we can utilize the water column pressure ($p$), which is defined as:
| $ p_t = p_0 + \rho_w g h $ |
This results in:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
As the height difference ($\Delta h$) is:
| $ \Delta h = h_2 - h_1 $ |
the pressure difference ($\Delta p$) can be expressed as:
| $ \Delta p = \rho_w g \Delta h $ |
ID:(15704, 0)
Pressure difference
Description
When two columns of liquid with different heights are connected, it can generate a pressure difference that leads to a flow of liquid from the taller column to the shorter one. This movement continues until both columns reach the same height, eliminating any pressure difference.
Variables
Calculations
to 
,
then, select the variable: 
to 
Calculations
Variable
Given
Calculate
Target :
Equation
To be used
Equations
As the the column force ($F$) generated by a column of liquid of the column height ($h$), the column Section ($S$), the liquid density ($\rho_w$), and the gravitational Acceleration ($g$) is
| $ F = S h \rho_w g $ |
and the the water column pressure ($p$) is then defined as
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
we have that the the water column pressure ($p$) generated by a column of liquid is
| $ p = \rho_w g h $ |
(ID 4249)
As the the column force ($F$) generated by a column of liquid of the column height ($h$), the column Section ($S$), the liquid density ($\rho_w$), and the gravitational Acceleration ($g$) is
| $ F = S h \rho_w g $ |
and the the water column pressure ($p$) is then defined as
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
we have that the the water column pressure ($p$) generated by a column of liquid is
| $ p = \rho_w g h $ |
(ID 4249)
(ID 4252)
If there is the pressure difference ($\Delta p$) between two points, as determined by the equation:
| $ dp = p - p_0 $ |
we can utilize the water column pressure ($p$), which is defined as:
| $ p_t = p_0 + \rho_w g h $ |
This results in:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
As the height difference ($\Delta h$) is:
| $ \Delta h = h_2 - h_1 $ |
the pressure difference ($\Delta p$) can be expressed as:
| $ \Delta p = \rho_w g \Delta h $ |
(ID 4345)
Examples
(ID 15478)
If two columns of water with different heights at their bases are connected, a situation arises where there is a pressure difference along the connecting tube.
This setup allows us to study how the pressure difference generates a liquid flow along the tube. We can consider an element of liquid with a certain length and a section equal to that of the tube, and estimate the corresponding mass using the density. With the section, we can also convert the pressure difference into a force difference and, ultimately, study how volumes in liquids are accelerated due to pressure differences.
(ID 933)
If there is the pressure difference ($\Delta p$) between two points, as determined by the equation:
| $ dp = p - p_0 $ |
we can utilize the water column pressure ($p$), which is defined as:
| $ p_t = p_0 + \rho_w g h $ |
This results in:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
As the height difference ($\Delta h$) is:
| $ \Delta h = h_2 - h_1 $ |
the pressure difference ($\Delta p$) can be expressed as:
| $ \Delta p = \rho_w g \Delta h $ |
(ID 15704)
(ID 15479)
ID:(1608, 0)