Benützer:
Druckunterschied
Storyboard 
Wenn zwei Säulen aus Flüssigkeit mit unterschiedlichen Höhen miteinander verbunden werden, kann dies einen Druckunterschied erzeugen, der zu einem Fluss von Flüssigkeit von der höheren zur niedrigeren Säule führt. Diese Bewegung setzt sich fort, bis beide Säulen die gleiche Höhe erreichen und somit keinen Druckunterschied mehr aufweisen.
ID:(1608, 0)
Anschließen von zwei Flüssigkeitsäulen
Konzept
Wenn zwei Säulen mit Wasser unterschiedlicher Höhe an ihren Basen verbunden werden, entsteht eine Situation, in der entlang des Verbindungsröhrs ein Druckunterschied herrscht.
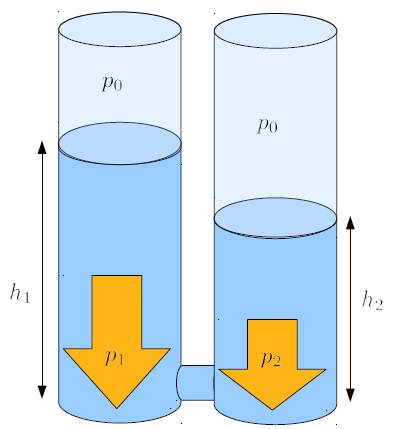
Diese Einrichtung ermöglicht es uns, zu studieren, wie der Druckunterschied einen Flüssigkeitsfluss entlang des Rohrs erzeugt. Wir können ein Element der Flüssigkeit mit einer bestimmten Länge und einer Querschnittsfläche, die der des Rohrs entspricht, betrachten und die entsprechende Masse unter Verwendung der Dichte abschätzen. Mit der Querschnittsfläche können wir auch den Druckunterschied in einen Kraftunterschied umrechnen und letztendlich untersuchen, wie Volumina in Flüssigkeiten aufgrund von Druckunterschieden beschleunigt werden.
ID:(933, 0)
Druckunterschied zwischen Säulen
Konzept
Wenn zwischen zwei Punkten die Druckunterschied ($\Delta p$) existiert, wie durch die Gleichung bestimmt:
| $ dp = p - p_0 $ |
können wir die Druck der Wassersäule ($p$) verwenden, definiert als:
| $ p_t = p_0 + \rho_w g h $ |
Dies ergibt:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Da die Höhendifferenz ($\Delta h$) wie folgt definiert ist:
| $ \Delta h = h_2 - h_1 $ |
kann die Druckunterschied ($\Delta p$) wie folgt ausgedrückt werden:
| $ \Delta p = \rho_w g \Delta h $ |
ID:(15704, 0)
Druckunterschied
Beschreibung
Wenn zwei Säulen aus Flüssigkeit mit unterschiedlichen Höhen miteinander verbunden werden, kann dies einen Druckunterschied erzeugen, der zu einem Fluss von Flüssigkeit von der höheren zur niedrigeren Säule führt. Diese Bewegung setzt sich fort, bis beide Säulen die gleiche Höhe erreichen und somit keinen Druckunterschied mehr aufweisen.
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
Da die die Kraft der Säule ($F$), die von einer Fl ssigkeitss ule von die Höhe der Säule ($h$), die Column Abschnitt ($S$), die Flüssigkeitsdichte ($\rho_w$) und die Gravitationsbeschleunigung ($g$) erzeugt wird, ist
| $ F = S h \rho_w g $ |
und die die Druck der Wassersäule ($p$) dann definiert ist als
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
haben wir, dass die von einer Fl ssigkeitss ule erzeugte die Druck der Wassersäule ($p$) ist
| $ p = \rho_w g h $ |
(ID 4249)
Da die die Kraft der Säule ($F$), die von einer Fl ssigkeitss ule von die Höhe der Säule ($h$), die Column Abschnitt ($S$), die Flüssigkeitsdichte ($\rho_w$) und die Gravitationsbeschleunigung ($g$) erzeugt wird, ist
| $ F = S h \rho_w g $ |
und die die Druck der Wassersäule ($p$) dann definiert ist als
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
haben wir, dass die von einer Fl ssigkeitss ule erzeugte die Druck der Wassersäule ($p$) ist
| $ p = \rho_w g h $ |
(ID 4249)
(ID 4252)
Wenn zwischen zwei Punkten die Druckunterschied ($\Delta p$) existiert, wie durch die Gleichung bestimmt:
| $ dp = p - p_0 $ |
k nnen wir die Druck der Wassersäule ($p$) verwenden, definiert als:
| $ p_t = p_0 + \rho_w g h $ |
Dies ergibt:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Da die Höhendifferenz ($\Delta h$) wie folgt definiert ist:
| $ \Delta h = h_2 - h_1 $ |
kann die Druckunterschied ($\Delta p$) wie folgt ausgedr ckt werden:
| $ \Delta p = \rho_w g \Delta h $ |
(ID 4345)
Beispiele
(ID 15478)
Wenn zwei S ulen mit Wasser unterschiedlicher H he an ihren Basen verbunden werden, entsteht eine Situation, in der entlang des Verbindungsr hrs ein Druckunterschied herrscht.
Diese Einrichtung erm glicht es uns, zu studieren, wie der Druckunterschied einen Fl ssigkeitsfluss entlang des Rohrs erzeugt. Wir k nnen ein Element der Fl ssigkeit mit einer bestimmten L nge und einer Querschnittsfl che, die der des Rohrs entspricht, betrachten und die entsprechende Masse unter Verwendung der Dichte absch tzen. Mit der Querschnittsfl che k nnen wir auch den Druckunterschied in einen Kraftunterschied umrechnen und letztendlich untersuchen, wie Volumina in Fl ssigkeiten aufgrund von Druckunterschieden beschleunigt werden.
(ID 933)
Wenn zwischen zwei Punkten die Druckunterschied ($\Delta p$) existiert, wie durch die Gleichung bestimmt:
| $ dp = p - p_0 $ |
k nnen wir die Druck der Wassersäule ($p$) verwenden, definiert als:
| $ p_t = p_0 + \rho_w g h $ |
Dies ergibt:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Da die Höhendifferenz ($\Delta h$) wie folgt definiert ist:
| $ \Delta h = h_2 - h_1 $ |
kann die Druckunterschied ($\Delta p$) wie folgt ausgedr ckt werden:
| $ \Delta p = \rho_w g \Delta h $ |
(ID 15704)
(ID 15479)
ID:(1608, 0)