Proceso de mezcla en aguas profundas
Storyboard 
En mayores profundidades, los mecanismos de disipación de energía de los vórtices están relacionados con la viscosidad y la flotabilidad. Cuál de estos domina depende de la situación y puede determinarse mediante los números característicos asociados a ambos fenómenos.
[1] Marine Physics, Jerzy Dera, Elsevier, 1992 (6.2 The Turbulent Exchange of Mass, Heat and Momentum in the Sea)
ID:(1628, 0)
Proceso de mezcla en aguas profundas
Storyboard 
En mayores profundidades, los mecanismos de disipación de energía de los vórtices están relacionados con la viscosidad y la flotabilidad. Cuál de estos domina depende de la situación y puede determinarse mediante los números característicos asociados a ambos fenómenos. [1] Marine Physics, Jerzy Dera, Elsevier, 1992 (6.2 The Turbulent Exchange of Mass, Heat and Momentum in the Sea)
Variables
Cálculos
Cálculos
Ecuaciones
Como la energía disipada por viscosidad ($\epsilon_{\eta}$) de los v rtices est relacionado con la viscosidad del agua oceánica ($\eta$), la velocidad del vórtice ($v_l$) y la longitud de mezcla ($l$),
$\epsilon_{\eta} =\eta\displaystyle\frac{v_l}{l}$
la p rdida de energ a por la tiempo característico ($\tau$), que es
se expresa como
Como la energía disipada por flotación ($\epsilon_{\rho}$) es igual a ERROR:9484, la aceleración gravitacional ($g$) y la distancia recorrida ($\Delta z$),
$\epsilon_{\rho} =\Delta\rho g \Delta z$
la p rdida de energ a ser esta energ a por la tiempo característico ($\tau$), que con la longitud de mezcla ($l$) es
por lo que con la velocidad del vórtice ($v_l$) es
En el caso de que los procesos difusivos sean m s relevantes que los de flotaci n, se tiene que con la energía cinética ($\epsilon_v$), la energía disipada por flotación ($\epsilon_{\rho}$) y la energía disipada por viscosidad ($\epsilon_{\eta}$),
$\epsilon_v > \epsilon_{\eta} \gg \epsilon_{\rho}$
Dado que con la tiempo característico ($\tau$), la energía cinética ($\epsilon_v$) y la densidad del medio ($\rho$) es
y la energía disipada por viscosidad ($\epsilon_{\eta}$) es
la existencia del v rtice implica que su energ a cin tica es mayor que la p rdida, por lo que con
$\rho\displaystyle\frac{v_l^3}{l}>\eta\displaystyle\frac{v_l^2}{l^2}$
resulta la exigencia de que se tenga que el número de Reynold ($Re$) es
En el caso de que con la energía cinética ($\epsilon_v$), la energía disipada por viscosidad ($\epsilon_{\eta}$) y la energía disipada por flotación ($\epsilon_{\rho}$) sean tales que
$\epsilon_v > \epsilon_{\rho} \gg \epsilon_{\eta}$
Dado que la energía cinética ($\epsilon_v$) es con la densidad del medio ($\rho$), la longitud de mezcla ($l$) y la velocidad del vórtice ($v_l$) en la tiempo característico ($\tau$),
y la energía disipada por flotación ($\epsilon_{\rho}$) es con ERROR:9484, la aceleración gravitacional ($g$) y la velocidad del vórtice ($v_l$) en la tiempo característico ($\tau$),
la existencia del v rtice implica que su energ a cin tica es mayor que la p rdida, por lo que con
$\rho\displaystyle\frac{v_l^3}{l}>\Delta\rho g v_l$
resulta la exigencia de que con se tiene que el número de Richardson ($R_i$) satisfaga
Como la energía cinética ($\epsilon_v$) del v rtices depende de la densidad del medio ($\rho$) y la velocidad del vórtice ($v_l$) seg n
$\epsilon_v =\displaystyle\frac{1}{2}\rho v_l^2\sim \rho v_l^2$
Como la tiempo característico ($\tau$) con la longitud de mezcla ($l$) es
se tiene que
$\displaystyle\frac{\epsilon_v}{\tau} =\rho \displaystyle\frac{v_l^3}{l}$
osea
Ejemplos
En general, la disipaci n de energ a ocurre en funci n del tiempo considerado, por lo que se debe comparar la energía cinética ($\epsilon_v$) con una tiempo característico ($\tau$), de modo que
$\displaystyle\frac{d\epsilon}{dt}\sim\displaystyle\frac{\epsilon_v}{\tau}$
Existen dos tipos de proceso que reducen la energ a de los v rtices hasta que pasan a ser fluctuaciones t rmicas. Por un lado est la difusi n del momento o viscosidad mientras que por el otro lado est la flotaci n.
La p rdida de la energía cinética ($\epsilon_v$) var a en funci n de la energía disipada por viscosidad ($\epsilon_{\eta}$) y la energía disipada por flotación ($\epsilon_{\rho}$) en la tiempo característico ($\tau$) es
Como la energía cinética ($\epsilon_v$), donde por simplicidad descartamos el factor de 1/2 y depende de la densidad del medio ($\rho$) y la velocidad del vórtice ($v_l$),
$\epsilon =\displaystyle\frac{1}{2}\rho v_l^2\sim \rho v_l^2$
la p rdida de energ a ser esta energ a por la tiempo característico ($\tau$), que con la longitud de mezcla ($l$) es
y as , la variaci n es
Como la energía disipada por viscosidad ($\epsilon_{\eta}$) est con la viscosidad del agua oceánica ($\eta$), la velocidad del vórtice ($v_l$) y la longitud de mezcla ($l$),
$\epsilon_{\eta} =\eta\displaystyle\frac{v_l}{l}$
la p rdida de energ a ser esta energ a por la tiempo característico ($\tau$), que con la longitud de mezcla ($l$) es
y as , la variaci n es
Como la energía disipada por flotación ($\epsilon_{\rho}$) est relacionado con ERROR:9484, la aceleración gravitacional ($g$) y la longitud de mezcla ($l$):
$\epsilon_{\rho} =\Delta\rho g l$
la p rdida de energ a ser esta energ a por la tiempo característico ($\tau$), que es
y as , la variaci n es
En el caso de que los procesos difusivos sean m s relevantes que los de flotaci n, se tiene que con la energía cinética ($\epsilon_v$), la energía disipada por flotación ($\epsilon_{\rho}$) y la energía disipada por viscosidad ($\epsilon_{\eta}$),
$\epsilon_v > \epsilon_{\eta} \gg \epsilon_{\rho}$
Dado que con la tiempo característico ($\tau$), la energía cinética ($\epsilon_v$) es
y la energía disipada por viscosidad ($\epsilon_{\eta}$) es
la existencia del v rtice implica que su energ a cin tica es mayor que la p rdida, por lo que con
$\rho\displaystyle\frac{v_l^3}{l}>\eta\displaystyle\frac{v_l^2}{l^2}$
resulta la exigencia de que se tenga que
En el caso de que con la energía cinética ($\epsilon_v$), la energía disipada por viscosidad ($\epsilon_{\eta}$) y la energía disipada por flotación ($\epsilon_{\rho}$) sean tales que
$\epsilon_v > \epsilon_{\rho} \gg \epsilon_{\eta}$
Dado que la energía cinética ($\epsilon_v$) es con la densidad ($\rho$), la longitud de mezcla ($l$) y la velocidad del vórtice ($v_l$) en la tiempo característico ($\tau$),
y la energía disipada por flotación ($\epsilon_{\rho}$) es con ERROR:9484, la aceleración gravitacional ($g$) y la velocidad del vórtice ($v_l$) en la tiempo característico ($\tau$),
la existencia del v rtice implica que su energ a cin tica es mayor que la p rdida, por lo que con
$\rho\displaystyle\frac{v_l^3}{l}>\Delta\rho g v_l$
resulta la exigencia de que con se tiene que el número de Richardson ($R_i$) satisfaga
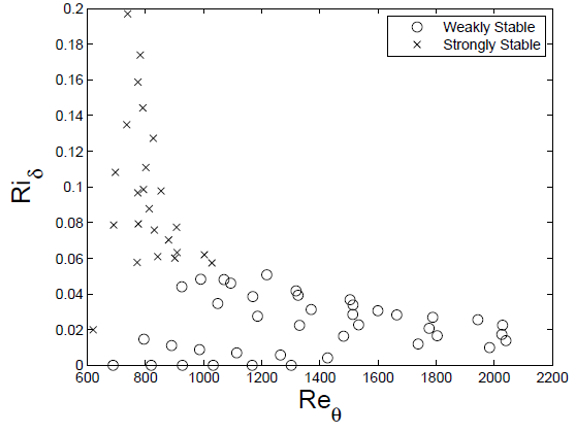
La relaci n entre ERROR:8614 con la densidad ($\rho$), la velocidad del vórtice ($v_l$), la viscosidad del agua oceánica ($\eta$) y la tamaño característico ($l$) est dada por
y el número de Richardson ($R_i$) con ERROR:9484 y la aceleración gravitacional ($g$) est representada por
como se muestra en el gr fico a continuaci n, donde ambos casos l mite marcan las situaciones de l mite de estabilidad:
Existen dos tipos de proceso que reducen la energ a de los v rtices hasta que pasan a ser fluctuaciones t rmicas. Por un lado est la difusi n del momento o viscosidad mientras que por el otro lado est la flotaci n.
La p rdida de la energía cinética ($\epsilon_v$) var a en funci n de la energía disipada por viscosidad ($\epsilon_{\eta}$) y la energía disipada por flotación ($\epsilon_{\rho}$) en la tiempo característico ($\tau$) es
Con la velocidad del vórtice ($v_l$) y la longitud de mezcla ($l$), se puede definir una tiempo característico ($\tau$), lo que permite estimar la p rdida de energ a tanto por viscosidad como flotaci n.
Por lo tanto, se tiene que
La variaci n de la energía cinética ($\epsilon_v$) en la tiempo característico ($\tau$) es proporcional a la energ a cin tica que depende de la densidad del medio ($\rho$) y la velocidad del vórtice ($v_l$), dividida por la tiempo característico ($\tau$). Dado que esta es una funci n de la longitud de mezcla ($l$), se concluye que:
La p rdida debido a la viscosidad del agua se puede calcular directamente a partir de la fuerza viscosa y la distancia recorrida por el v rtice.
La p rdida de la energía disipada por viscosidad ($\epsilon_{\eta}$) var a en funci n de la viscosidad del agua oceánica ($\eta$), la velocidad del vórtice ($v_l$) y la longitud de mezcla ($l$). En la tiempo característico ($\tau$), se expresa como
La p rdida debido a la flotaci n se puede calcular directamente a partir de la fuerza de sustentaci n y la distancia recorrida por el v rtice.
La p rdida de la energía disipada por flotación ($\epsilon_{\rho}$) var a en funci n de ERROR:9484, la aceleración gravitacional ($g$) y la velocidad del vórtice ($v_l$). En la tiempo característico ($\tau$), se expresa como
En el caso de que con la energía cinética ($\epsilon_v$), la energía disipada por viscosidad ($\epsilon_{\eta}$) y la energía disipada por flotación ($\epsilon_{\rho}$) sean tales que
$\epsilon_v > \epsilon_{\eta} \gg \epsilon_{\rho}$
se tiene que la amortiguaci n es ante todo debido a la viscosidad.
En ese caso, se obtiene una condici n para el número de Reynold ($Re$), que es una funci n de la densidad del medio ($\rho$), la velocidad del vórtice ($v_l$), la tamaño característico ($l$) y la viscosidad del agua oceánica ($\eta$), que debe satisfacer
En el caso de que con la energía cinética ($\epsilon_v$), la energía disipada por viscosidad ($\epsilon_{\eta}$) y la energía disipada por flotación ($\epsilon_{\rho}$) sean tales que
$\epsilon_v > \epsilon_{\rho} \gg \epsilon_{\eta}$
se tiene que la amortiguaci n es principalmente debido a la flotabilidad.
En ese caso, se obtiene una condici n para el número de Richardson ($R_i$), que es una funci n de ERROR:9484, la densidad del medio ($\rho$), la velocidad del vórtice ($v_l$), la aceleración gravitacional ($g$) y la longitud de mezcla ($l$), que debe satisfacer
ID:(1628, 0)