Procesos de mezcla en aguas poco profundas
Storyboard 
Los mecanismos de mezcla en áreas poco profundas son generados por diversos tipos de olas. Entre ellos se encuentran las olas internas, las olas superficiales, la interacción entre olas y corrientes, las mareas y el rompimiento de olas en la costa.
ID:(1629, 0)
Procesos de mezcla en aguas poco profundas
Storyboard 
Los mecanismos de mezcla en áreas poco profundas son generados por diversos tipos de olas. Entre ellos se encuentran las olas internas, las olas superficiales, la interacción entre olas y corrientes, las mareas y el rompimiento de olas en la costa.
Variables
Cálculos
Cálculos
Ecuaciones
As como la estrés cinemático ($\tau_x$) se relaciona con la viscosidad turbulenta ($A$) y la longitud de mezcla ($l$), se obtiene que:
Si se emplean la constante de Karman ($\kappa$), la profundidad total ($H$) y la rugosidad ($k$):
y con la velocidad en fricción ($U_d$):
se tiene:
De la misma manera que la estrés cinemático ($\tau_x$) se relaciona con la viscosidad turbulenta ($A$), el perfil de la velocidad ($u_z$) y la profundidad ($z$) se define mediante
se puede integrar desde el desniveles ($d$) hasta la profundidad ($z$) para obtener la velocidad mediante la siguiente expresi n:
$u_z=\displaystyle\int_d^z\displaystyle\frac{\tau_x}{A}dz'$
Con la formulaci n de la viscosidad turbulenta ($A$) en funci n de la profundidad relativa ($\xi$) junto con la profundidad total ($H$), la rugosidad ($k$) y la velocidad en fricción ($U_d$), y considerando que
se deriva la siguiente ecuaci n para la velocidad:
$u_z=\displaystyle\frac{U_d\sqrt{1-k}}{\kappa}(\ln(z/d) + \Phi(\xi,k))$
donde
$\Phi=2[\arctan(\lambda)-\arctan(\lambda_0)]-\ln\left(\displaystyle\frac{1+\lambda}{1+\lambda_0}\right)$
se define con
$\lambda=\sqrt{1-\xi}$
y
$\lambda=\sqrt{1-k}$
Dado que a lo largo de la mayor parte de la profundidad
$\ln(z/d) \gg \Phi(\xi,k)$
el perfil de velocidad se puede simplificar a
Como la fuerza viscosa ($F_v$) de las superficies paralelas ($S$), la viscosidad ($\eta$), la diferencia de velocidad entre superficies ($\Delta v$) y la distancia entre las superficies ($\Delta z$) mediante:
se tiene que el analogo a la fuerza por area y densidad $\rho$ es
$\displaystyle\frac{F_v}{S\rho}=\tau_x$
y el analogo a la viscosidad y densidad es
$\displaystyle\frac{\eta}{\rho}=A$
por lo que resulta en la anlog a
Los sedimentos tienden a caer al fondo con una velocidad de sedimentación ($\omega_s$), mientras que la difusi n, que en este caso corresponde a la mezcla generada por los torbellinos, induce un flujo igual a la viscosidad turbulenta ($A$) y el gradiente de el concentración de sedimentos ($c_z$) en la profundidad ($z$) de la siguiente forma:
$A\displaystyle\frac{\partial c_z}{\partial z}+\omega_s c_z= 0$
Si se integra esta expresi n, se obtiene:
$c_z = \displaystyle\frac{E}{\omega_s}e^{-\displaystyle\int_d^z \omega_s/A dz'}$
con la longitud de mezcla ($l$):
se tiene:
$c_z=\displaystyle\frac{E}{\omega_s}e^{-\displaystyle\int_d^z \omega_s/l\sqrt{\tau_x} dz'}$
lo que resulta en:
$c_z=\displaystyle\frac{E}{\omega_s}\left(\displaystyle\frac{z}{d}\right)^{R_s}\Phi_c(\xi,k)$
con el factor de Rouse ($R_s$) y el número de Rouse ($R_0$):
donde:
$\Phi=\left(\displaystyle\frac{1+\lambda}{1+\lambda_0}\right)^{2R_s}e^{2R_s[\arctan(\lambda)-\arctan(\lambda_0)]}$
con:
$\lambda=\sqrt{1-\xi}$
y:
$\lambda=\sqrt{1-k}$
Como en gran parte de la profundidad:
$\Phi\sim 1$
se tiene la distribuci n de la concentraci n:
As como la viscosidad turbulenta ($A$) se relaciona con la longitud de mezcla ($l$), el perfil de la velocidad ($u_z$) y la profundidad ($z$) se define como
y dado que la estrés cinemático ($\tau_x$) es
si se elimina el gradiente, se obtiene
Ejemplos
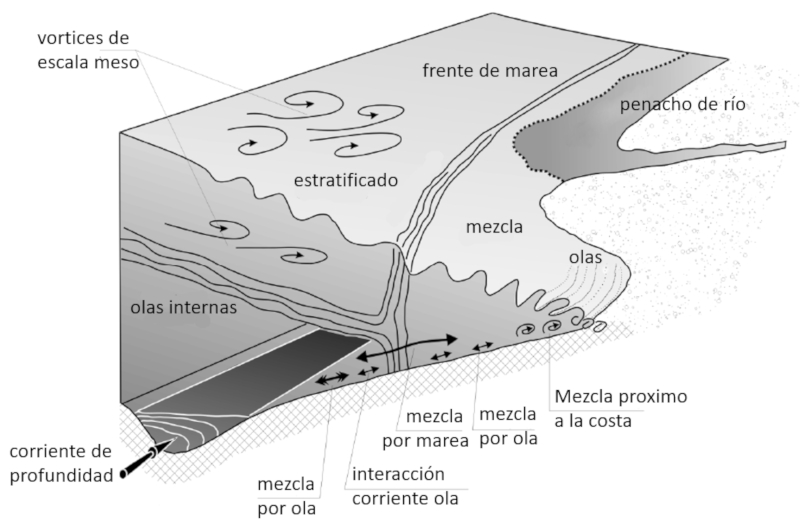
Para el caso en el borde costero en donde hay baja profundidad se tienen los siguientes mecanismos que contribuyen el mezclado de las aguas por efecto de:
• olas internas
adicionalmente existen contribuciones adicionales mediante
• mezcla por ola
• interacci n de corriente con olas
• mezcla por mares
• mezcla por quiebre de olas en costa
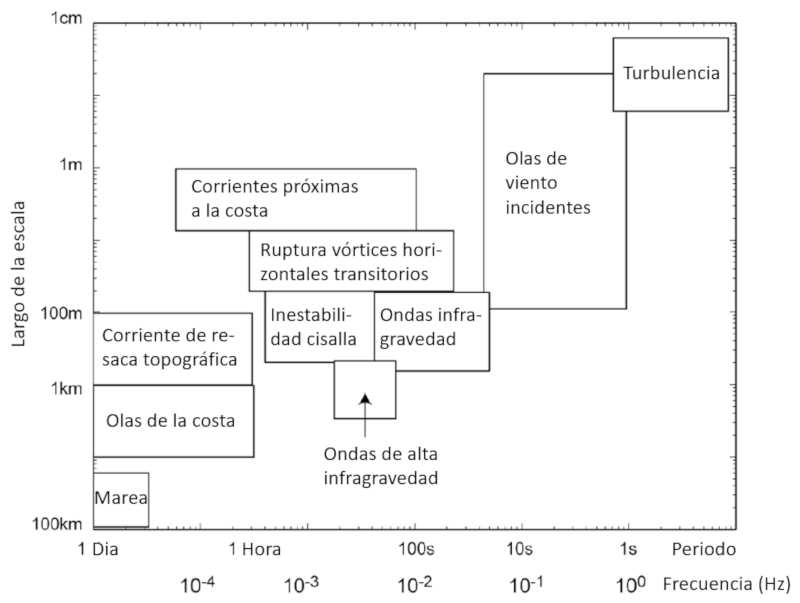
Las perturbaciones se pueden ordenar en funci n de sus escalas de tiempo y dimensiones. El resultado se presenta en la siguiente grafica:
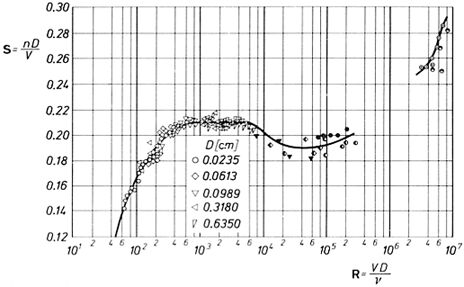
El número de Strouhal ($St$) se relaciona de forma emp rica con el número de Reynold ($Re$). El número de Strouhal ($St$) est asociado con la frecuencia de generación de vortices ($\omega$), la velocidad en fricción ($U_d$), y la profundidad total ($H$) es
Esto permite estimar, a trav s de el número de Reynold ($Re$), la frecuencia con la que la concentraci n puede intercambiar los componentes a difundir. Sin embargo, hay que tener presente que el proceso puede ser interrumpido si la frecuencia es menor que la de las mareas.
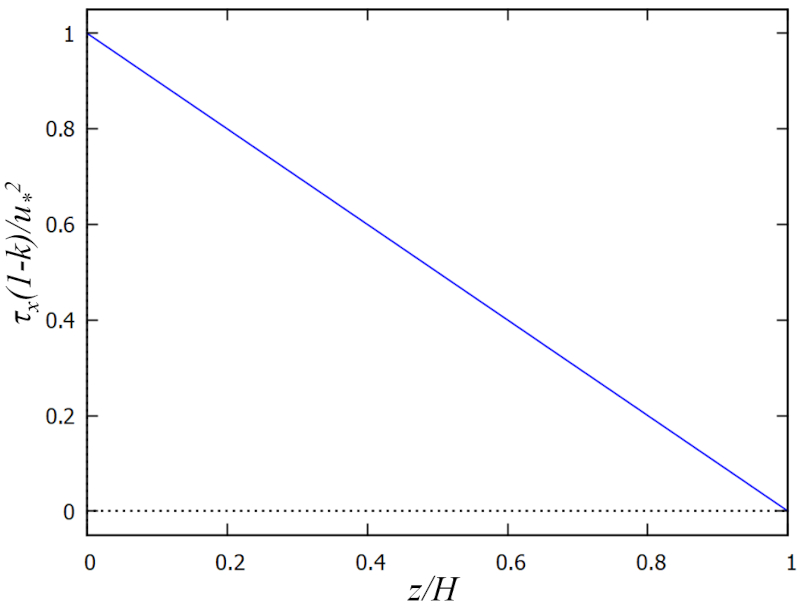
Si se asume que no hay viento sobre la superficie, se puede suponer que no existe tensi n en esta. Por lo tanto, solo habr tensi n del agua sobre el fondo. Esta tensi n disminuir linealmente desde el fondo hasta la superficie. Para simplificar el modelamiento, se puede trabajar con la proporci n entre la profundidad ($z$) y la profundidad total ($H$), lo que nos proporciona un factor adimensional la profundidad relativa ($\xi$). La estrés cinemático ($\tau_x$) ser , por ende, proporcional a
$\tau_x \propto 1-\xi$
Dado que la estrés cinemático ($\tau_x$) es equivalente a la densidad de energ a dividida por la densidad, el valor en el fondo debe ser proporcional al cuadrado de la velocidad en el fondo. Esta ltima se describe en el modelo con la velocidad en fricción ($U_d$) y significa que
$\tau_x \propto U_d^2$
Por ltimo, se tiene el efecto de la rugosidad ($k$) del fondo marino, es decir, la proporci n de el desniveles ($d$) y la profundidad total ($H$). Esto lleva a que la estrés cinemático ($\tau_x$) se debe corregir por un factor an logo al de profundidad:
$\tau_x \propto \displaystyle\frac{1-\xi}{1-k}$
Con esto, se obtiene un modelo de la siguiente forma:
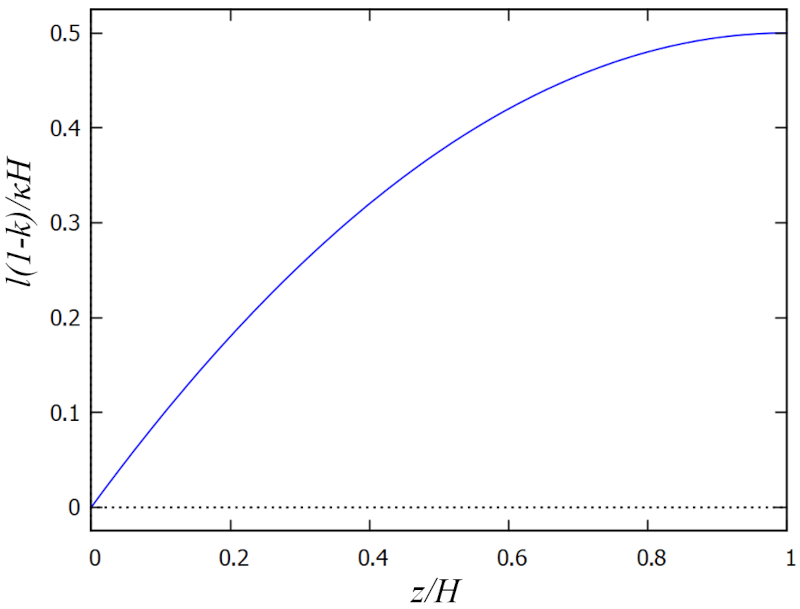
que se grafica a continuaci n:
La longitud de mezcla ($l$) corresponde al tama o de los v rtices. En la proximidad de la pared, estos solo pueden tener un tama o m ximo igual a la distancia a la pared, lo cual es m nimo. A medida que nos acercamos a la superficie, estos pueden ser cada vez m s grandes, por lo que la funci n debe alcanzar un m ximo en este punto.
Para simplificar la modelizaci n, se puede trabajar con la proporci n entre la profundidad ($z$) y la profundidad total ($H$), lo que nos proporciona un factor adimensional la profundidad relativa ($\xi$). De esta forma, una funci n simple que cumple con esta descripci n es de la forma:
$l \propto \xi\left(1-\displaystyle\frac{1}{2}\xi\right)$
Por otro lado, el modelo de capa superficial de Prandtl muestra que estas son una fracci n del flujo con un ancho igual a la profundidad total ($H$) y una proporci n de la constante de Karman ($\kappa$), por lo que:
$l \propto \kappa H$
Finalmente, debemos corregir por el efecto de la rugosidad de la misma forma que se realiza para el estr s cinem tico:
$l \propto \displaystyle\frac{\kappa H}{1-k}$
Por lo tanto, la longitud de mezcla ($l$) se puede modelar mediante:
Cuando Prandtl modela la formaci n de torbellinos en la proximidad de las paredes, establece la relaci n entre la viscosidad turbulenta ($A$), la longitud de mezcla ($l$), y el gradiente de el perfil de la velocidad ($u_z$) en la profundidad ($z$) de la siguiente forma:
Por otro lado, la fuerza viscosa t pica, que se modela como la viscosidad multiplicada por la superficie de contacto y el gradiente de la velocidad, corresponde en el caso de las turbulencias a la estrés cinemático ($\tau_x$):
De ambas ecuaciones surge la relaci n:
Esta relaci n permite calcular la viscosidad turbulenta ($A$) en funci n de la estrés cinemático ($\tau_x$) y la longitud de mezcla ($l$), que se modelan en este caso. Se obtiene as con la profundidad total ($H$), la velocidad en fricción ($U_d$), la rugosidad ($k$), la profundidad relativa ($\xi$), y la constante de Karman ($\kappa$):
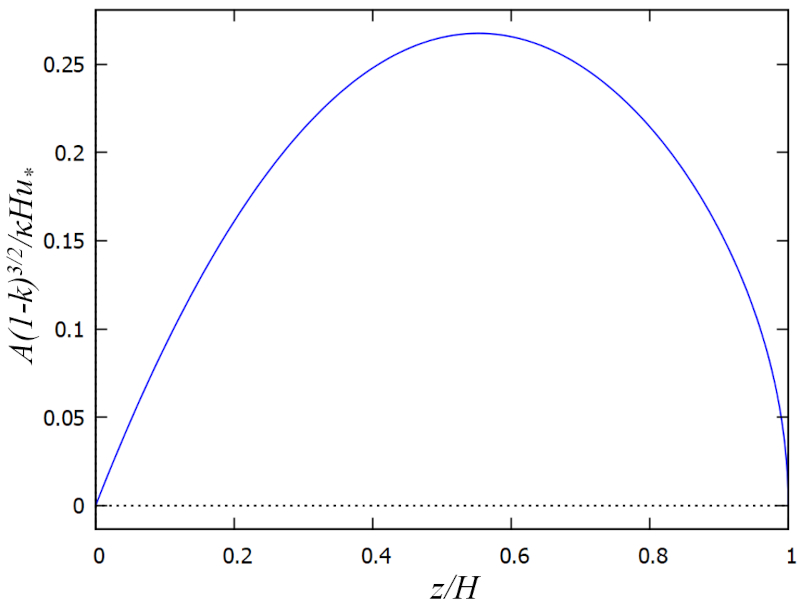
que se representa a continuaci n:
El resultado es que la viscosidad turbulenta es m xima a media profundidad y se reduce a valores m nimos tanto cerca del fondo como cerca de la superficie. Es decir, en estas zonas el mezclado y la p rdida de momento son menores.
Dado que la estrés cinemático ($\tau_x$) es igual a la viscosidad turbulenta ($A$) y al gradiente de el perfil de la velocidad ($u_z$) respecto de la profundidad ($z$), es posible integrar la ecuaci n para obtener el perfil de velocidad:
$u_z = \displaystyle\int_d^z \frac{\tau_x}{A} dz'$
Al realizar esta integraci n, y utilizando la velocidad en fricción ($U_d$), la constante de Karman ($\kappa$), la rugosidad ($k$) y la profundidad relativa ($\xi$), se obtiene:
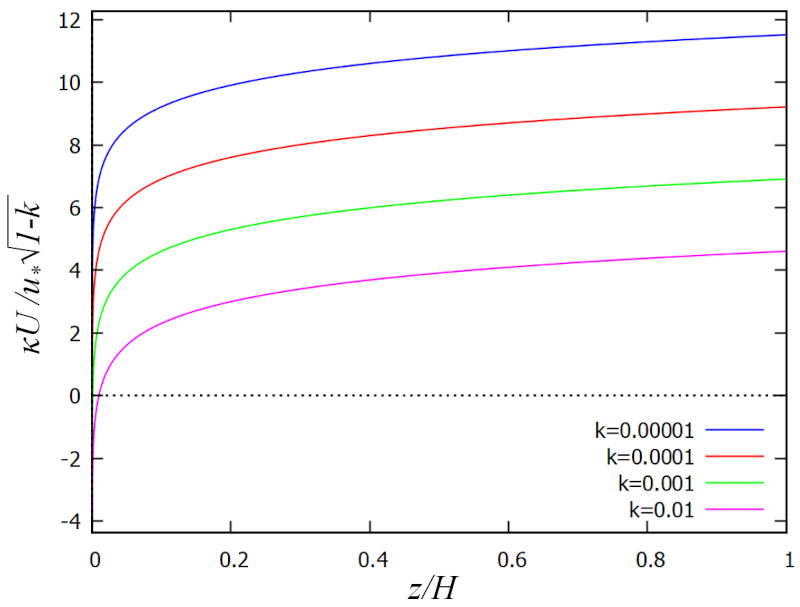
Esta expresi n corresponde a la conocida ley logar tmica del perfil de velocidades, desarrollada por Prandtl y Schlichting.
El resultado se visualiza en la siguiente gr fica:
Este perfil tambi n permite establecer una relaci n entre el velocidad en la superficie ($U$) y la velocidad en fricción ($U_d$) en funci n de la coeficiente de arrastre ($C_D$):
A su vez, la coeficiente de arrastre ($C_D$) puede estimarse a partir de la rugosidad ($k$) y la constante de Karman ($\kappa$) mediante:
Si se considera el comportamiento del material suspendido, se observar que por un lado existe la tendencia a sedimentar con una velocidad la velocidad de sedimentación ($\omega_s$), generando un flujo que depende de el concentración de sedimentos ($c_z$), expresado como:
$\omega_s c_z$
Por otro lado, los torbellinos tienden a mezclar el agua, generando una difusi n que lleva los sedimentos hacia la superficie. Este flujo, representado con la viscosidad turbulenta ($A$), es dado por el gradiente de el concentración de sedimentos ($c_z$) en la profundidad ($z$), igual a:
$A\displaystyle\frac{\partial c_z}{\partial z}$
La distribuci n se forma cuando los sedimentos alcanzan el equilibrio, siendo igual el flujo de sedimentaci n a la difusi n generada por los torbellinos hacia la superficie. Integrando ambos t rminos de la ecuaci n con el tasa de erosión ($E$) y el desniveles ($d$), se obtiene la distribuci n:
$c_z=\displaystyle\frac{E}{\omega_s}e^{\displaystyle\int_d^z \omega_s/A dz'}$
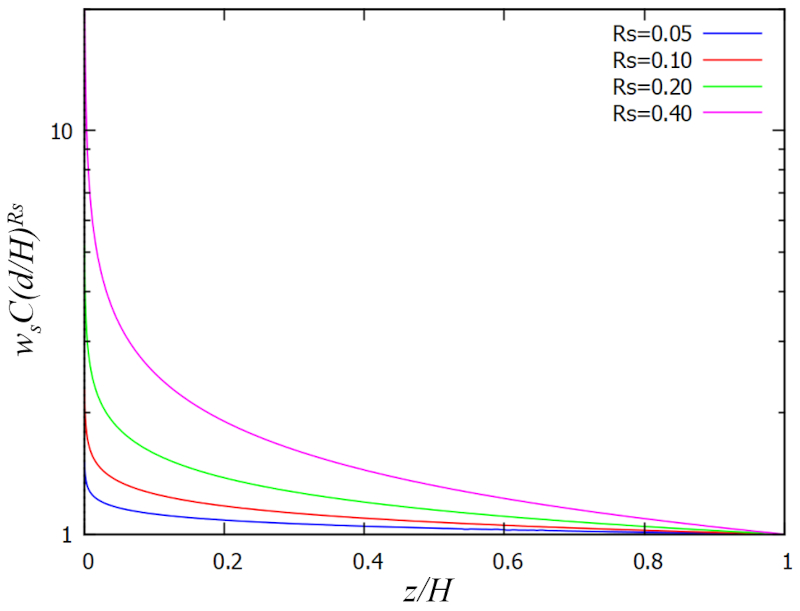
Despu s de emplear la expresi n obtenida para la viscosidad turbulenta ($A$) con el factor de Rouse ($R_s$), la rugosidad ($k$) y la profundidad relativa ($\xi$), se obtiene la expresi n:
lo cual se puede representar gr ficamente como:
El número de Strouhal ($St$) caracteriza la frecuencia de generación de vortices ($\omega$). Compara la velocidad asociada a la frecuencia de generación de vortices ($\omega$) y su tama o con el del flujo representado por la profundidad total ($H$).
Por tanto, con ello, tenemos
El comportamiento de la corriente y las turbulencias a generar o amortiguar depende de la rugosidad ($k$) del fondo marino. Esto se define comparando el perfil medio de el desniveles ($d$) con el perfil de la profundidad total ($H$) en el que se encuentra.
Por lo tanto, se define que la rugosidad ($k$) es
La profundidad relativa ($\xi$) se define en funci n de la profundidad ($z$) y la profundidad total ($H$), expresado de la siguiente manera:
Para un flujo laminar, la fuerza viscosa ($F_v$) se puede calcular a partir de las superficies paralelas ($S$), la viscosidad ($\eta$), la diferencia de velocidad entre superficies ($\Delta v$) y la distancia entre las superficies ($\Delta z$) utilizando la siguiente f rmula:
En el caso de flujo turbulento, se establece una analog a definiendo una viscosidad turbulenta ($A$) como la viscosidad dividida por la densidad, asociada a la fuerza por rea y densidad, a lo que llamaremos la estrés cinemático ($\tau_x$), calculado en funci n de el perfil de la velocidad ($u_z$) y la profundidad ($z$) de la siguiente manera:
En 1925, Prandtl [1] introdujo el concepto de una capa l mite donde los torbellinos mezclan el fluido y transfieren momento de manera similar a como se modela la transferencia a nivel molecular, generando comportamiento viscoso. El tama o de esta zona se define como la longitud de mezcla ($l$) y el efecto se describe con un an logo a la viscosidad que corresponde a la viscosidad turbulenta ($A$). Esto se puede estimar mediante el gradiente de el perfil de la velocidad ($u_z$) en la profundidad ($z$) utilizando:
[1] Prandtl, Ludwig (1925). "Bericht ber Untersuchungen zur ausgebildeten Turbulenz" (Informe sobre investigaciones en turbulencia desarrollada). Z. Angew. Math. Mech. 5 (2): 136.
La estrés cinemático ($\tau_x$) se puede calcular a partir de la viscosidad turbulenta ($A$) y la longitud de mezcla ($l$) utilizando el siguiente m todo:
La estrés cinemático ($\tau_x$) alcanzar su m ximo cerca del fondo y ser nulo en la superficie, siempre y cuando no haya viento en la superficie del oc ano. Dado que en el fondo est asociado con la velocidad en fricción ($U_d$), pero necesita correcci n por el efecto de la rugosidad ($k$), se puede modelar en funci n de la profundidad relativa ($\xi$) de la siguiente manera:
La zona de mezcla introducida por Prandtl, de tama o la longitud de mezcla ($l$), se estima como una fracci n del orden de la constante de Karman ($\kappa$) de la profundidad total ($H$). Adem s, se debe ajustar por el efecto de la rugosidad ($k$), y considerar que la longitud de mezcla ($l$) depende de la profundidad relativa ($\xi$), siendo nulo en el fondo y aproximadamente constante y m ximo cerca de la superficie. Por lo tanto, se puede modelar de la siguiente manera:
[1] Prandtl, Ludwig (1925). "Bericht ber Untersuchungen zur ausgebildeten Turbulenz" (Informe sobre investigaciones en turbulencia desarrollada). Z. Angew. Math. Mech. 5 (2): 136.
A partir de mediciones, podemos modelar la viscosidad turbulenta ($A$) con la profundidad relativa ($\xi$), la profundidad total ($H$), la rugosidad ($k$), la velocidad en fricción ($U_d$) y la constante de Karman ($\kappa$) mediante la expresi n:
El perfil de la velocidad ($u_z$) es una funci n de la profundidad relativa ($\xi$) y los par metros la rugosidad ($k$), la velocidad en fricción ($U_d$) y la constante de Karman ($\kappa$), representada de la forma siguiente:
El velocidad en la superficie ($U$) es proporcional a la velocidad en fricción ($U_d$), con una constante de proporcionalidad que depende de la constante de Karman ($\kappa$) y la rugosidad ($k$), seg n:
La velocidad en fricción ($U_d$) es proporcional a el velocidad en la superficie ($U$), con una constante de proporci n la coeficiente de arrastre ($C_D$), que representa la relaci n entre las respectivas energ as cin ticas:
El concentración de sedimentos ($c_z$) es una funci n de la profundidad relativa ($\xi$) que depende de el tasa de erosión ($E$), la velocidad de sedimentación ($\omega_s$), la rugosidad ($k$) y el factor de Rouse ($R_s$), y se calcula de la siguiente manera:
El valor el número de Rouse ($R_0$) compara la velocidad de sedimentaci n, que rivaliza con la difusi n relacionada con la corriente en el fondo. Al combinarlo con la velocidad de sedimentación ($\omega_s$), la velocidad en fricción ($U_d$) y la constante de Karman ($\kappa$) se obtiene:
El valor el número de Rouse ($R_0$) eval a la velocidad de sedimentaci n, que compite con la difusi n vinculada a la corriente en el fondo. En combinaci n con la velocidad de sedimentación ($\omega_s$), la velocidad en fricción ($U_d$) y la constante de Karman ($\kappa$) se deriva:
En situaciones donde el fondo marino no es uniforme, existe la rugosidad ($k$), lo que requiere una correcci n del n mero de Rouse, a la que llamamos factor de Rouse:
ID:(1629, 0)