Deep water mixing process
Storyboard 
In the case of greater depths, the energy dissipation mechanisms of vortices are related to viscosity and buoyancy. Which one dominates depends on the situation and can be determined using characteristic numbers associated with both phenomena.
[1] Marine Physics, Jerzy Dera, Elsevier, 1992 (6.2 The Turbulent Exchange of Mass, Heat and Momentum in the Sea)
ID:(1628, 0)
Deep water mixing process
Storyboard 
In the case of greater depths, the energy dissipation mechanisms of vortices are related to viscosity and buoyancy. Which one dominates depends on the situation and can be determined using characteristic numbers associated with both phenomena. [1] Marine Physics, Jerzy Dera, Elsevier, 1992 (6.2 The Turbulent Exchange of Mass, Heat and Momentum in the Sea)
Variables
Calculations
Calculations
Equations
The loss from the vortices involves the energy dissipated by viscosity ($\epsilon_{\eta}$) with the viscosity of ocean water ($\eta$), the vortex speed ($v_l$), and the mixing length ($l$).
$\epsilon_{\eta} =\eta\displaystyle\frac{v_l}{l}$
The energy loss due to the characteristic time ($\tau$), which is
is described by
Since the energy dissipated by flotation ($\epsilon_{\rho}$) equals ERROR:9484, the gravitational Acceleration ($g$), and the distance traveled ($\Delta z$),
$\epsilon_{\rho} =\Delta\rho g \Delta z$
the energy loss will be this energy per the characteristic time ($\tau$), which, with the mixing length ($l$), is
so with the vortex speed ($v_l$), it is
In the case where diffusive processes are more relevant than buoyancy, we have that with the kinetic energy ($\epsilon_v$), the energy dissipated by flotation ($\epsilon_{\rho}$) and the energy dissipated by viscosity ($\epsilon_{\eta}$),
$\epsilon_v > \epsilon_{\eta} \gg \epsilon_{\rho}$
Given that with the characteristic time ($\tau$), the kinetic energy ($\epsilon_v$) and the medium density ($\rho$) is
and the energy dissipated by viscosity ($\epsilon_{\eta}$) is
the existence of the vortex implies that its kinetic energy is greater than the loss, so with
$\rho\displaystyle\frac{v_l^3}{l}>\eta\displaystyle\frac{v_l^2}{l^2}$
the requirement that the reynolds number ($Re$) must be
In the event that with the kinetic energy ($\epsilon_v$), the energy dissipated by viscosity ($\epsilon_{\eta}$), and the energy dissipated by flotation ($\epsilon_{\rho}$) are such that
$\epsilon_v > \epsilon_{\rho} \gg \epsilon_{\eta}$
Given that the kinetic energy ($\epsilon_v$) is with the medium density ($\rho$), the mixing length ($l$), and the vortex speed ($v_l$) in the characteristic time ($\tau$),
and the energy dissipated by flotation ($\epsilon_{\rho}$) is with ERROR:9484, the gravitational Acceleration ($g$), and the vortex speed ($v_l$) in the characteristic time ($\tau$),
the existence of the vortex implies that its kinetic energy is greater than the loss, so with
$\rho\displaystyle\frac{v_l^3}{l}>\Delta\rho g v_l$
the requirement arises that with, the richardson number ($R_i$) must satisfy
Como the kinetic energy ($\epsilon_v$) of the vortices depends on the medium density ($\rho$) and the vortex speed ($v_l$) according to
$\epsilon_v =\displaystyle\frac{1}{2}\rho v_l^2\sim \rho v_l^2$
Como the characteristic time ($\tau$) with the mixing length ($l$) is
we have that
$\displaystyle\frac{\epsilon_v}{\tau} =\rho \displaystyle\frac{v_l^3}{l}$
which means
Examples
In general, energy dissipation occurs over the considered time period, so the kinetic energy ($\epsilon_v$) should be compared with a characteristic time ($\tau$) such that
$\displaystyle\frac{d\epsilon}{dt}\sim\displaystyle\frac{\epsilon_v}{\tau}$
There are two types of processes that reduce the energy of vortices until they become thermal fluctuations. On one hand, there's momentum diffusion or viscosity, while on the other hand, there's flotation.
The loss of the kinetic energy ($\epsilon_v$) varies depending on the energy dissipated by viscosity ($\epsilon_{\eta}$) and the energy dissipated by flotation ($\epsilon_{\rho}$) in the characteristic time ($\tau$) as
As the kinetic energy ($\epsilon_v$), where for simplicity we neglect the factor of 1/2 and it depends on the medium density ($\rho$) and the vortex speed ($v_l$),
$\epsilon =\displaystyle\frac{1}{2}\rho v_l^2\sim \rho v_l^2$
the energy loss will be this energy by the characteristic time ($\tau$), which with the mixing length ($l$) is
and thus, the variation is
As the energy dissipated by viscosity ($\epsilon_{\eta}$) is with the viscosity of ocean water ($\eta$), the vortex speed ($v_l$), and the mixing length ($l$),
$\epsilon_{\eta} =\eta\displaystyle\frac{v_l}{l}$
the energy loss will be this energy by the characteristic time ($\tau$), which with the mixing length ($l$) is
and thus, the variation is
As the energy dissipated by flotation ($\epsilon_{\rho}$) is with ERROR:9484, the gravitational acceleration ($g$), and the mixing length ($l$):
$\epsilon_{\rho} =\Delta\rho g l$
the energy loss will be this energy by the characteristic time ($\tau$), which is
and thus, the variation is
In the case where diffusive processes are more relevant than flotation ones, it is observed that with the kinetic energy ($\epsilon_v$), the energy dissipated by flotation ($\epsilon_{\rho}$), and the energy dissipated by viscosity ($\epsilon_{\eta}$),
$\epsilon_v > \epsilon_{\eta} \gg \epsilon_{\rho}$
Given that with the characteristic time ($\tau$), the kinetic energy ($\epsilon_v$) is
and the energy dissipated by viscosity ($\epsilon_{\eta}$) is
the existence of the vortex implies that its kinetic energy is greater than the loss, so with
$\rho\displaystyle\frac{v_l^3}{l}>\eta\displaystyle\frac{v_l^2}{l^2}$
it results in the requirement that it must be the case that
In the event that with the kinetic energy ($\epsilon_v$), the energy dissipated by viscosity ($\epsilon_{\eta}$), and the energy dissipated by flotation ($\epsilon_{\rho}$) are such that
$\epsilon_v > \epsilon_{\rho} \gg \epsilon_{\eta}$
Given that the kinetic energy ($\epsilon_v$) is with the density ($\rho$), the mixing length ($l$), and the vortex speed ($v_l$) in the characteristic time ($\tau$),
and the energy dissipated by flotation ($\epsilon_{\rho}$) is with ERROR:9484, the gravitational Acceleration ($g$), and the vortex speed ($v_l$) in the characteristic time ($\tau$),
the existence of the vortex implies that its kinetic energy is greater than the loss, so with
$\rho\displaystyle\frac{v_l^3}{l}>\Delta\rho g v_l$
the requirement arises that with it must be the case that the richardson number ($R_i$) satisfies
The relationship between ERROR:8614 with the density ($\rho$), the vortex speed ($v_l$), the viscosity of ocean water ($\eta$), and the tamaño característico ($l$) is given by
and the richardson number ($R_i$) with ERROR:9484 and the gravitational Acceleration ($g$) is represented by
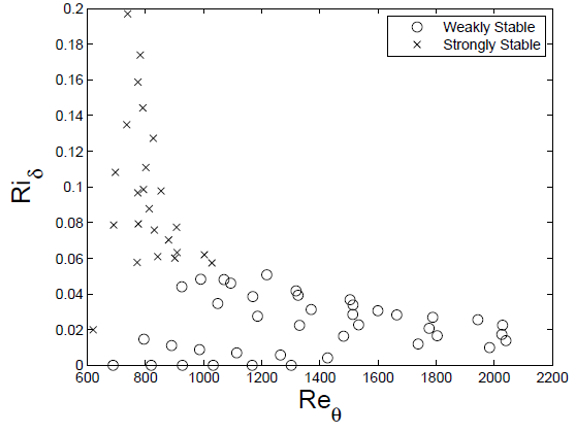
as shown in the graph below, where both boundary cases mark the stability limit situations:
There are two types of processes that reduce the energy of vortices until they become thermal fluctuations. On one hand, there's momentum diffusion or viscosity, while on the other hand, there's flotation.
The loss of the kinetic energy ($\epsilon_v$) varies depending on the energy dissipated by viscosity ($\epsilon_{\eta}$) and the energy dissipated by flotation ($\epsilon_{\rho}$) in the characteristic time ($\tau$) as
With the vortex speed ($v_l$) and the mixing length ($l$), one can define a characteristic time ($\tau$), which allows estimating the energy loss both due to viscosity and flotation.
Therefore, it follows that
The variation of the kinetic energy ($\epsilon_v$) in the characteristic time ($\tau$) is proportional to the kinetic energy, which depends on the medium density ($\rho$) and the vortex speed ($v_l$), divided by the characteristic time ($\tau$). Since this is a function of the mixing length ($l$), it follows that:
The loss due to water viscosity can be calculated directly from the viscous force and the path traveled by the vortex.
The loss of the energy dissipated by viscosity ($\epsilon_{\eta}$) varies depending on the viscosity of ocean water ($\eta$), the vortex speed ($v_l$), and the mixing length ($l$). In the characteristic time ($\tau$), it is expressed as
The loss due to buoyancy can be calculated directly from the lift force and the distance traveled by the vortex.
The loss of the energy dissipated by flotation ($\epsilon_{\rho}$) varies depending on ERROR:9484, the gravitational Acceleration ($g$), and the vortex speed ($v_l$). In the characteristic time ($\tau$), it is expressed as
In the event that with the kinetic energy ($\epsilon_v$), the energy dissipated by viscosity ($\epsilon_{\eta}$), and the energy dissipated by flotation ($\epsilon_{\rho}$) are such that
$\epsilon_v > \epsilon_{\eta} \gg \epsilon_{\rho}$
the damping is primarily due to viscosity.
In that case, a condition is obtained for the reynolds number ($Re$), which is a function of the medium density ($\rho$), the vortex speed ($v_l$), the tamaño característico ($l$), and the viscosity of ocean water ($\eta$), which must satisfy
In the event that with the kinetic energy ($\epsilon_v$), the energy dissipated by viscosity ($\epsilon_{\eta}$), and the energy dissipated by flotation ($\epsilon_{\rho}$) are such that
$\epsilon_v > \epsilon_{\rho} \gg \epsilon_{\eta}$
the damping is primarily due to buoyancy.
In that case, a condition is obtained for the richardson number ($R_i$), which is a function of ERROR:9484, the medium density ($\rho$), the vortex speed ($v_l$), the gravitational Acceleration ($g$), and the mixing length ($l$), which must satisfy
ID:(1628, 0)