Campo eléctrico
Storyboard 
Como las cargas generan fuerzas, una distribución de cargas actuara sobre una carga que uno posiciones en cualquier punto del espacio. En otras palabras existe un 'campo' es decir una fuerza en cualquier punto del espacio. Esta fuerza depende de la carga que expongamos por lo que tiene sentido definir una fuerza por carga de modo que sea independiente de la carga de la partícula la que buscamos estudiar su comportamiento. Por ello es posible definir lo que llamamos un campo eléctrico que es la suma total de todas las fuerzas de Coulomb de las cargas distribuidas dividio por la carga de la partícula de la que se esta estudiando el comportamiento.
ID:(814, 0)
Campo eléctrico
Storyboard 
Como las cargas generan fuerzas, una distribución de cargas actuara sobre una carga que uno posiciones en cualquier punto del espacio. En otras palabras existe un 'campo' es decir una fuerza en cualquier punto del espacio. Esta fuerza depende de la carga que expongamos por lo que tiene sentido definir una fuerza por carga de modo que sea independiente de la carga de la partícula la que buscamos estudiar su comportamiento. Por ello es posible definir lo que llamamos un campo eléctrico que es la suma total de todas las fuerzas de Coulomb de las cargas distribuidas dividio por la carga de la partícula de la que se esta estudiando el comportamiento.
Variables
Cálculos
Cálculos
Ecuaciones
La fuerza ($\vec{F}$) sobre la carga de prueba ($q$) en la posición ($\vec{r}$) depender de el número de cargas ($N$), contabilizado con el ndice $i$, representado por la carga del ion i ($Q_i$) ubicado en la posición de una carga i ($\vec{u}_i$). Con los par metros la constante dieléctrica ($\epsilon$) y la constante de campo eléctrico ($\epsilon_0$), esto se puede escribir como:
Con la definici n de el campo eléctrico ($\vec{E}$) dada por
se tiene que el campo el ctrico de una distribuci n de cargas es
La magnitud de la fuerza con masa constante ($F$) generada entre dos cargas, representadas por la carga de prueba ($q$) y la carga ($Q$), que se encuentran a una distancia de la distancia ($r$), se calcula utilizando la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$) de la siguiente manera:
Con la definici n del campo el ctrico como
se obtiene
Ejemplos
Para medir la fuerza de Coulomb, se necesita introducir una carga de prueba en el sistema. Si dicha carga es la carga de prueba ($q$), se puede estimar la fuerza por unidad de carga que las cargas del sistema ejercen sobre la carga de prueba. La magnitud de la fuerza la fuerza ($\vec{F}$) por unidad de carga la carga de prueba ($q$) se denomina campo el ctrico el campo eléctrico ($\vec{E}$) y se mide en Newtons (N) por Coulomb (C). El campo el ctrico se mide asumiendo que la carga de prueba no perturba significativamente el sistema; en otras palabras, se supone que esta es muy peque a. La definici n del campo se puede escribir como:
En el caso en que la geometr a permita trabajar de forma unidimensional, se puede definir la fuerza con masa constante ($F$) por la carga de prueba ($q$) introduciendo el campo eléctrico ($E$), lo cual se expresa como:
La magnitud de la fuerza con masa constante ($F$) generada entre dos cargas, representadas por la carga de prueba ($q$) y la carga ($Q$), que se encuentran a una distancia de la distancia ($r$), se calcula utilizando la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$) de la siguiente manera:
Con la definici n del campo el ctrico como
se obtiene
La fuerza ($\vec{F}$) sobre la carga de prueba ($q$) en la posición ($\vec{r}$) depender de el número de cargas ($N$), contabilizado con el ndice $i$, representado por la carga del ion i ($Q_i$) ubicado en la posición de una carga i ($\vec{u}_i$). Con los par metros la constante dieléctrica ($\epsilon$) y la constante de campo eléctrico ($\epsilon_0$), esto se puede escribir como:
Con la definici n de el campo eléctrico ($\vec{E}$) dada por
se tiene que el campo el ctrico de una distribuci n de cargas es
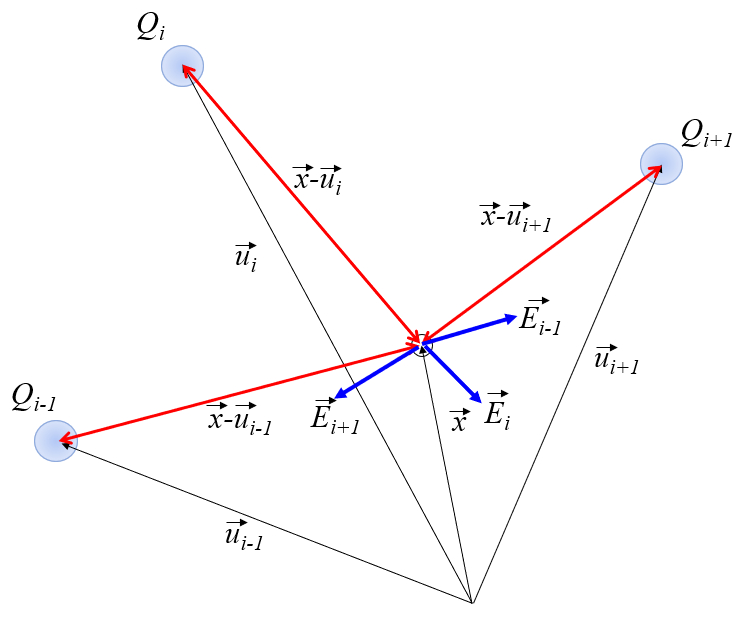
La ecuaci n se puede representar graficamente de la siguiente forma:
La fuerza ($\vec{F}$) por la carga de prueba ($q$) se define como el campo eléctrico ($\vec{E}$), lo cual se expresa como:
La fuerza con masa constante ($F$) por la carga de prueba ($q$) se define como el campo eléctrico ($E$), lo cual se expresa como:
Una vez que se conoce el campo eléctrico ($E$), se puede calcular la fuerza con masa constante ($F$), que act a sobre la carga ($q$), mediante:
Una vez que se conoce el campo eléctrico ($\vec{E}$), se puede calcular la fuerza ($\vec{F}$), que act a sobre la carga ($q$), mediante:
La magnitud de el campo eléctrico ($E$) generada por la carga ($Q$), que se encuentran a una distancia de la distancia ($r$), se calcula utilizando la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$) de la siguiente manera:
El campo eléctrico ($\vec{E}$) en la posición ($\vec{r}$) depender de el número de cargas ($N$), contabilizado con el ndice $i$ representado por la carga del ion i ($Q_i$), ubicado en la posición de una carga i ($\vec{u}_i$). Con los par metros la constante dieléctrica ($\epsilon$) y la constante de campo eléctrico ($\epsilon_0$), esto se puede expresar de la siguiente manera:
ID:(814, 0)