mechanisms

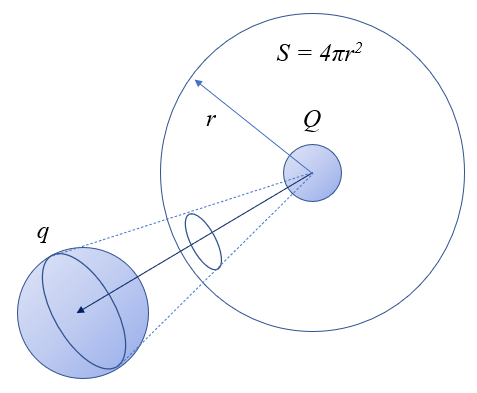
Una forma de comprender la naturaleza de la fuerza entre dos cargas es considerar que la interacci n se modela a trav s del intercambio de part culas, que en este caso son fotones. La cantidad de estos mensajeros es proporcional a la carga que los emite y tambi n a la probabilidad de que sean capturados por la otra carga. En ese sentido,

la fuerza deber a ser proporcional al producto de ambas cargas.

Por otro lado, estos mensajeros son emitidos en todas direcciones, distribuy ndose sobre una esfera imaginaria alrededor de la carga. La superficie de esta esfera es $4\pi r^2$, donde

r es el radio, correspondiente a la distancia entre las cargas. Por tanto,

la fuerza deber a ser inversamente proporcional al cuadrado de la distancia entre las cargas, es decir, inversamente proporcional a la superficie de la esfera centrada en la otra carga.

Esta distribuci n se puede visualizar gr ficamente como la superficie alrededor de una carga y el 'cono' dentro del cual los fotones son capturados por la otra carga.

image

As , la fuerza, como una magnitud escalar, tendr a la forma

$F \propto \displaystyle\frac{qQ}{4\pi r^2}$

La fuerza entre cargas el ctricas depende de:

• Las magnitudes de las cargas, siendo positiva si ambas cargas son del mismo signo y negativa si son de signos opuestos.
• La magnitud de la fuerza disminuye con el cuadrado de la distancia entre las cargas.
• La direcci n de la fuerza se alinea a lo largo de la l nea que conecta ambas cargas.

image

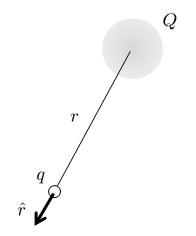
Por esta raz n, Coulomb [1] formul que la fuerza con masa constante ($F$) es proporcional al producto de las magnitudes de las cargas la carga de prueba ($q$) y la carga ($Q$), inversamente proporcional al cuadrado de la distancia ($r$) que las separa, con constantes de proporcionalidad la constante dieléctrica ($\epsilon$) y la constante de campo eléctrico ($\epsilon_0$):

equation=3212

La fuerza de Coulomb act a en la direcci n de la distancia ($r$), que se puede representar con el verson ($\hat{r}$). Por lo tanto, la ecuaci n anterior se puede generalizar como:

equation=15772

[1] "Premier M moire sur l lectricit et le Magn tisme" (Primera memoria sobre la electricidad y el magnetismo), Charles-Augustin de Coulomb, Acad mie Royale des Sciences en Par s, 1785.

La fuerza ($\vec{F}$), generada entre dos cargas representadas por la carga de prueba ($q$) y la carga ($Q$), que se encuentran a una distancia de la distancia ($r$), se calcula utilizando la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$). La direcci n es a lo largo de la distancia ($r$), lo que se puede representar mediante el verson ($\hat{r}$). Por lo tanto, la ley se expresa como:

equation=15772

Si se considera que la distancia ($r$) es la distancia entre la posición 1 ($\vec{s}_1$) y la posición 2 ($\vec{s}_2$), se puede expresar como:

equation=10390

y para el verson ($\hat{r}$), mediante:

equation=10391

Asociando la posición ($\vec{r}$) con la posición 2 ($\vec{s}_2$), la posición 1 ($\vec{s}_1$) con la posición de una carga i ($\vec{u}_i$) y la carga ($Q$) con la carga del ion i ($Q_i$), se puede concluir que el total de la fuerza ($\vec{F}$) es:

equation=10392

model

La distancia ($r$) representa la distancia entre la posición 1 ($\vec{s}_1$) y la posición 2 ($\vec{s}_2$), que se puede expresar como:

kyon

El verson ($\hat{r}$) a lo largo de la distancia entre la posición 1 ($\vec{s}_1$) y la posición 2 ($\vec{s}_2$) se puede calcular utilizando la siguiente f rmula:

kyon

La magnitud de la fuerza con masa constante ($F$) generada entre dos cargas, representadas por la carga de prueba ($q$) y la carga ($Q$), que se encuentran a una distancia de la distancia ($r$), se calcula utilizando la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$) de la siguiente manera:

kyon

La fuerza ($\vec{F}$), generada entre dos cargas representadas por la carga de prueba ($q$) y la carga ($Q$), que se encuentran a una distancia de la distancia ($r$), se calcula utilizando la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$). La direcci n es a lo largo de la distancia ($r$), lo que se puede representar mediante el verson ($\hat{r}$). Por lo tanto, la ley se escribe como:

kyon

La fuerza ($\vec{F}$) sobre la carga de prueba ($q$) en la posición ($\vec{r}$) depender de el número de cargas ($N$), contabilizado con el ndice $i$ representado por la carga del ion i ($Q_i$) ubicado en la posición de una carga i ($\vec{u}_i$). Con los par metros la constante dieléctrica ($\epsilon$) y la constante de campo eléctrico ($\epsilon_0$), esto se puede escribir como:

kyon