Elektrisches Feld
Storyboard 
Wenn Lasten Kräfte erzeugen, wirkt eine Lastverteilung auf eine Last, die an einem beliebigen Punkt im Raum positioniert wird. Mit anderen Worten, es gibt ein 'Feld', das an jedem Punkt im Raum eine Kraft ist. Diese Kraft hängt von der Ladung ab, die wir exponieren. Es ist daher sinnvoll, eine Kraft pro Ladung zu definieren, damit sie unabhängig von der Ladung des Teilchens ist, dessen Verhalten wir untersuchen möchten. Daher ist es möglich zu definieren, was wir ein elektrisches Feld nennen, das die Gesamtsumme aller Coulomb-Kräfte der verteilten Ladungen dividiert durch die Ladung des Teilchens, von dem aus das Verhalten untersucht wird.
ID:(814, 0)
Elektrisches Feld
Storyboard 
Wenn Lasten Kräfte erzeugen, wirkt eine Lastverteilung auf eine Last, die an einem beliebigen Punkt im Raum positioniert wird. Mit anderen Worten, es gibt ein 'Feld', das an jedem Punkt im Raum eine Kraft ist. Diese Kraft hängt von der Ladung ab, die wir exponieren. Es ist daher sinnvoll, eine Kraft pro Ladung zu definieren, damit sie unabhängig von der Ladung des Teilchens ist, dessen Verhalten wir untersuchen möchten. Daher ist es möglich zu definieren, was wir ein elektrisches Feld nennen, das die Gesamtsumme aller Coulomb-Kräfte der verteilten Ladungen dividiert durch die Ladung des Teilchens, von dem aus das Verhalten untersucht wird.
Variablen
Berechnungen
Berechnungen
Gleichungen
Die Kraft ($\vec{F}$) auf die Test Ladung ($q$) bei die Position ($\vec{r}$) h ngt von der Anzahl der Ladunegn ($N$) ab, die mit dem Index $i$ erfasst und durch die Ladung der Ionen i ($Q_i$) dargestellt wird, das sich bei die Position einer Ladung i ($\vec{u}_i$) befindet. Mit den Parametern die Dielektrizitätskonstante ($\epsilon$) und die Elektrische Feldkonstante ($\epsilon_0$) kann dies wie folgt geschrieben werden:
Mit der Definition von der Elektrisches Feld ($\vec{E}$) durch
ergibt sich, dass das elektrische Feld einer Ladungsverteilung
Die Gr e von die Kraft mit konstanter Masse ($F$), die zwischen zwei Ladungen erzeugt wird, dargestellt durch die Test Ladung ($q$) und die Ladung ($Q$), die sich in einem Abstand von die Entfernung ($r$) befinden, wird wie folgt unter Verwendung von die Elektrische Feldkonstante ($\epsilon_0$) und die Dielektrizitätskonstante ($\epsilon$) berechnet:
Mit der Definition des elektrischen Feldes als
erhalten wir
Beispiele
Um die Coulomb-Kraft zu messen, muss eine Probeladung in das System eingef hrt werden. Wenn diese Probeladung die Test Ladung ($q$) betr gt, kann die Kraft pro Ladungseinheit gesch tzt werden, die die Ladungen des Systems auf die Probeladung aus ben. Die Gr e der Kraft die Kraft ($\vec{F}$) pro Ladungseinheit die Test Ladung ($q$) wird als elektrisches Feld der Elektrisches Feld ($\vec{E}$) bezeichnet und in Newton (N) pro Coulomb (C) gemessen. Das elektrische Feld wird unter der Annahme gemessen, dass die Probeladung das System nicht wesentlich st rt; mit anderen Worten, es wird angenommen, dass sie sehr klein ist. Die Definition des Feldes kann wie folgt geschrieben werden:
Wenn die Geometrie eine eindimensionale Analyse erm glicht, kann die Kraft mit konstanter Masse ($F$) pro die Test Ladung ($q$) durch Einf hrung von der Elektrisches Feld ($E$) definiert werden, was wie folgt ausgedr ckt wird:
Die Gr e von die Kraft mit konstanter Masse ($F$), die zwischen zwei Ladungen erzeugt wird, dargestellt durch die Test Ladung ($q$) und die Ladung ($Q$), die sich in einem Abstand von die Entfernung ($r$) befinden, wird wie folgt unter Verwendung von die Elektrische Feldkonstante ($\epsilon_0$) und die Dielektrizitätskonstante ($\epsilon$) berechnet:
Mit der Definition des elektrischen Feldes als
erhalten wir
Die Kraft ($\vec{F}$) auf die Test Ladung ($q$) bei die Position ($\vec{r}$) h ngt von der Anzahl der Ladunegn ($N$) ab, die mit dem Index $i$ erfasst und durch die Ladung der Ionen i ($Q_i$) dargestellt wird, das sich bei die Position einer Ladung i ($\vec{u}_i$) befindet. Mit den Parametern die Dielektrizitätskonstante ($\epsilon$) und die Elektrische Feldkonstante ($\epsilon_0$) kann dies wie folgt geschrieben werden:
Mit der Definition von der Elektrisches Feld ($\vec{E}$) durch
ergibt sich, dass das elektrische Feld einer Ladungsverteilung
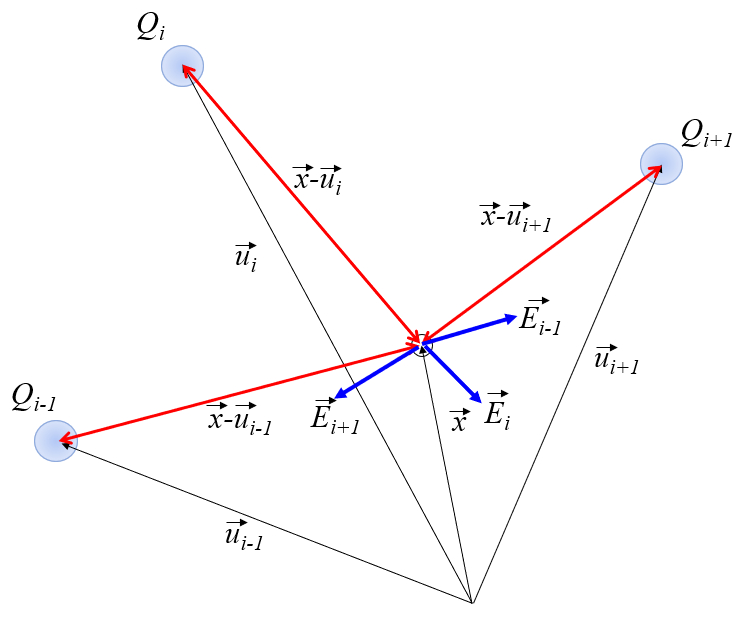
Die Gleichung kann grafisch wie folgt dargestellt werden:
Die Kraft ($\vec{F}$) f r die Test Ladung ($q$) ist als der Elektrisches Feld ($\vec{E}$) definiert, was ausgedr ckt wird als:
Die Kraft mit konstanter Masse ($F$) f r die Test Ladung ($q$) ist als der Elektrisches Feld ($E$) definiert, was ausgedr ckt wird als:
Sobald der Elektrisches Feld ($E$) bekannt ist, kann die Kraft mit konstanter Masse ($F$), das auf die Ladung ($q$) wirkt, berechnet werden mittels:
Sobald der Elektrisches Feld ($\vec{E}$) bekannt ist, kann die Kraft ($\vec{F}$), der auf die Ladung ($q$) wirkt, berechnet werden mit:
Die Gr e von der Elektrisches Feld ($E$), die durch die Ladung ($Q$) erzeugt wird und die sich in einem Abstand von die Entfernung ($r$) befinden, wird wie folgt unter Verwendung von die Elektrische Feldkonstante ($\epsilon_0$) und die Dielektrizitätskonstante ($\epsilon$) berechnet:
Der Elektrisches Feld ($\vec{E}$) bei die Position ($\vec{r}$) h ngt von der Anzahl der Ladunegn ($N$) ab, das mit dem Index $i$ erfasst und durch die Ladung der Ionen i ($Q_i$) dargestellt wird, das sich bei die Position einer Ladung i ($\vec{u}_i$) befindet. Mit den Parametern die Dielektrizitätskonstante ($\epsilon$) und die Elektrische Feldkonstante ($\epsilon_0$) kann dies wie folgt geschrieben werden:
ID:(814, 0)