User:
Coulomb law
Storyboard 
Charges exert forces on each other; if they are of the same sign, the force is repulsive, and if they are of opposite signs, it is attractive. This force is governed by Coulomb's Law and is proportional to the product of the magnitudes of the charges and inversely proportional to the square of the distance between them. The direction of the force is along the line that connects the two charges.
ID:(1497, 0)
Phenomenological description of the interaction between charges
Image
One way to understand the nature of the force between two charges is to consider that the interaction is modeled through the exchange of particles, which in this case are photons. The number of these messengers is proportional to the charge that emits them and also to the probability that they are captured by the other charge. In this sense,
the force should be proportional to the product of both charges.
On the other hand, these messengers are emitted in all directions, distributing over an imaginary sphere surrounding the charge. The surface area of this sphere is $4\pi r^2$, where
r is the radius, corresponding to the distance between the charges. Therefore,
the force should be inversely proportional to the square of the distance between the charges, that is, inversely proportional to the surface area of the sphere centered on the other charge.
This distribution can be visually represented as the surface around one charge and the 'cone' within which photons are captured by the other charge.
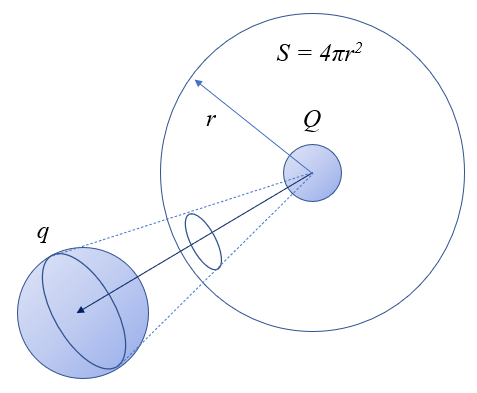
Thus, the force, as a scalar quantity, would take the form
$F \propto \displaystyle\frac{qQ}{4\pi r^2}$
ID:(11363, 0)
Coulomb force
Note
The force between electric charges depends on:
• The magnitudes of the charges, being positive if both charges have the same sign and negative if they have opposite signs.
• The magnitude of the force decreases with the square of the distance between the charges.
• The direction of the force aligns along the line that connects both charges.
For this reason, Coulomb [1] formulated that the force with constant mass ($F$) is proportional to the product of the magnitudes of the charges the test charge ($q$) and the charge ($Q$), inversely proportional to the square of the distance ($r$) separating them, with proportionality constants the dielectric constant ($\epsilon$) and the electric field constant ($\epsilon_0$):
| $ F =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2}$ |
The Coulomb force acts in the direction of the distance ($r$), which can be represented by the verson ($\hat{r}$). Therefore, the previous equation can be generalized as:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2} \hat{r} $ |
[1] "Premier Mémoire sur lÉlectricité et le Magnétisme" (First memory on electricity and magnetism), Charles-Augustin de Coulomb, Académie Royale des Sciences in Paris, 1785.
ID:(1697, 0)
Coulomb's law for a charge distribution
Quote
The force ($\vec{F}$), generated between two charges represented by the test charge ($q$) and the charge ($Q$), which are at a distance of the distance ($r$), is calculated using the electric field constant ($\epsilon_0$) and the dielectric constant ($\epsilon$). The direction is along the distance ($r$), which can be represented by the verson ($\hat{r}$). Therefore, the law is expressed as:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2} \hat{r} $ |
If the distance ($r$) is considered the distance between the position 1 ($\vec{s}_1$) and the position 2 ($\vec{s}_2$), it can be expressed as:
| $ r =| \vec{s}_2 - \vec{s}_1 |$ |
and for the verson ($\hat{r}$), using:
| $ \hat{r} =\displaystyle\frac{( \vec{s}_2 - \vec{s}_1 )}{| \vec{s}_2 - \vec{s}_1 |}$ |
By associating the position ($\vec{r}$) with the position 2 ($\vec{s}_2$), the position 1 ($\vec{s}_1$) with the position of a charge i ($\vec{u}_i$), and the charge ($Q$) with the charge of the ion i ($Q_i$), it can be concluded that the total the force ($\vec{F}$) is:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\sum_i^N\displaystyle\frac{ q Q_i }{| \vec{r} - \vec{u}_i |^3}( \vec{r} - \vec{u}_i )$ |
ID:(15773, 0)
Coulomb law
Description
Charges exert forces on each other; if they are of the same sign, the force is repulsive, and if they are of opposite signs, it is attractive. This force is governed by Coulomb's Law and is proportional to the product of the magnitudes of the charges and inversely proportional to the square of the distance between them. The direction of the force is along the line that connects the two charges.
Variables
Calculations
to 
,
then, select the variable: 
to 
Calculations
Variable
Given
Calculate
Target :
Equation
To be used
Equations
The force ($\vec{F}$), generated between two charges represented by the test charge ($q$) and the charge ($Q$), which are at a distance of the distance ($r$), is calculated using the electric field constant ($\epsilon_0$) and the dielectric constant ($\epsilon$). The direction is along the distance ($r$), which can be represented by the verson ($\hat{r}$). Therefore, the law is expressed as:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2} \hat{r} $ |
If the distance ($r$) is considered the distance between the position 1 ($\vec{s}_1$) and the position 2 ($\vec{s}_2$), it can be expressed as:
| $ r =| \vec{s}_2 - \vec{s}_1 |$ |
and for the verson ($\hat{r}$), using:
| $ \hat{r} =\displaystyle\frac{( \vec{s}_2 - \vec{s}_1 )}{| \vec{s}_2 - \vec{s}_1 |}$ |
By associating the position ($\vec{r}$) with the position 2 ($\vec{s}_2$), the position 1 ($\vec{s}_1$) with the position of a charge i ($\vec{u}_i$), and the charge ($Q$) with the charge of the ion i ($Q_i$), it can be concluded that the total the force ($\vec{F}$) is:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\sum_i^N\displaystyle\frac{ q Q_i }{| \vec{r} - \vec{u}_i |^3}( \vec{r} - \vec{u}_i )$ |
(ID 10392)
The magnitude of the force with constant mass ($F$) generated between two charges, represented by the test charge ($q$) and the charge ($Q$), which are at a distance of the distance ($r$), is calculated using the electric field constant ($\epsilon_0$) and the dielectric constant ($\epsilon$) as follows:
| $ F =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2}$ |
To model the force ($\vec{F}$) between charges in vector form, one must include the direction in which it acts, defined by the verson ($\hat{r}$), resulting in:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2} \hat{r} $ |
(ID 15772)
Examples
(ID 15264)
One way to understand the nature of the force between two charges is to consider that the interaction is modeled through the exchange of particles, which in this case are photons. The number of these messengers is proportional to the charge that emits them and also to the probability that they are captured by the other charge. In this sense,
the force should be proportional to the product of both charges.
On the other hand, these messengers are emitted in all directions, distributing over an imaginary sphere surrounding the charge. The surface area of this sphere is $4\pi r^2$, where
r is the radius, corresponding to the distance between the charges. Therefore,
the force should be inversely proportional to the square of the distance between the charges, that is, inversely proportional to the surface area of the sphere centered on the other charge.
This distribution can be visually represented as the surface around one charge and the 'cone' within which photons are captured by the other charge.
Thus, the force, as a scalar quantity, would take the form
$F \propto \displaystyle\frac{qQ}{4\pi r^2}$
(ID 11363)
The force between electric charges depends on:
• The magnitudes of the charges, being positive if both charges have the same sign and negative if they have opposite signs.
• The magnitude of the force decreases with the square of the distance between the charges.
• The direction of the force aligns along the line that connects both charges.
For this reason, Coulomb [1] formulated that the force with constant mass ($F$) is proportional to the product of the magnitudes of the charges the test charge ($q$) and the charge ($Q$), inversely proportional to the square of the distance ($r$) separating them, with proportionality constants the dielectric constant ($\epsilon$) and the electric field constant ($\epsilon_0$):
| $ F =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2}$ |
The Coulomb force acts in the direction of the distance ($r$), which can be represented by the verson ($\hat{r}$). Therefore, the previous equation can be generalized as:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2} \hat{r} $ |
[1] "Premier M moire sur l lectricit et le Magn tisme" (First memory on electricity and magnetism), Charles-Augustin de Coulomb, Acad mie Royale des Sciences in Paris, 1785.
(ID 1697)
The force ($\vec{F}$), generated between two charges represented by the test charge ($q$) and the charge ($Q$), which are at a distance of the distance ($r$), is calculated using the electric field constant ($\epsilon_0$) and the dielectric constant ($\epsilon$). The direction is along the distance ($r$), which can be represented by the verson ($\hat{r}$). Therefore, the law is expressed as:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2} \hat{r} $ |
If the distance ($r$) is considered the distance between the position 1 ($\vec{s}_1$) and the position 2 ($\vec{s}_2$), it can be expressed as:
| $ r =| \vec{s}_2 - \vec{s}_1 |$ |
and for the verson ($\hat{r}$), using:
| $ \hat{r} =\displaystyle\frac{( \vec{s}_2 - \vec{s}_1 )}{| \vec{s}_2 - \vec{s}_1 |}$ |
By associating the position ($\vec{r}$) with the position 2 ($\vec{s}_2$), the position 1 ($\vec{s}_1$) with the position of a charge i ($\vec{u}_i$), and the charge ($Q$) with the charge of the ion i ($Q_i$), it can be concluded that the total the force ($\vec{F}$) is:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\sum_i^N\displaystyle\frac{ q Q_i }{| \vec{r} - \vec{u}_i |^3}( \vec{r} - \vec{u}_i )$ |
(ID 15773)
(ID 15323)
The distance ($r$) represents the distance between the position 1 ($\vec{s}_1$) and the position 2 ($\vec{s}_2$), which can be expressed as:
| $ r =| \vec{s}_2 - \vec{s}_1 |$ |
(ID 10390)
The verson ($\hat{r}$) along the distance between the position 1 ($\vec{s}_1$) and the position 2 ($\vec{s}_2$) can be calculated using the following formula:
| $ \hat{r} =\displaystyle\frac{( \vec{s}_2 - \vec{s}_1 )}{| \vec{s}_2 - \vec{s}_1 |}$ |
(ID 10391)
The magnitude of the force with constant mass ($F$) generated between two charges, represented by the test charge ($q$) and the charge ($Q$), which are at a distance of the distance ($r$), is calculated using the electric field constant ($\epsilon_0$) and the dielectric constant ($\epsilon$) as follows:
| $ F =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2}$ |
(ID 3212)
The force ($\vec{F}$), generated between two charges represented by the test charge ($q$) and the charge ($Q$), which are at a distance of the distance ($r$), is calculated using the electric field constant ($\epsilon_0$) and the dielectric constant ($\epsilon$). The direction is along the distance ($r$), which can be represented by the verson ($\hat{r}$). Therefore, the law is written as:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2} \hat{r} $ |
(ID 15772)
The force ($\vec{F}$) on the test charge ($q$) at the position ($\vec{r}$) will depend on the number of charges ($N$) accounted for with the index $i$ represented by the charge of the ion i ($Q_i$) located at the position of a charge i ($\vec{u}_i$). With the parameters the dielectric constant ($\epsilon$) and the electric field constant ($\epsilon_0$), this can be expressed as:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\sum_i^N\displaystyle\frac{ q Q_i }{| \vec{r} - \vec{u}_i |^3}( \vec{r} - \vec{u}_i )$ |
(ID 10392)
ID:(1497, 0)