Énergie cinétique de rotation
Storyboard 
L'énergie cinétique de rotation est une fonction de la vitesse angulaire atteinte grâce à l'application d'un couple pendant un certain temps tout en parcourant un angle donné.
Ainsi, l'énergie cinétique de rotation est proportionnelle au moment d'inertie de l'objet et au carré de la vitesse angulaire.
ID:(1417, 0)
Barre qui tourne autour d'un axe $\perp$
Image 
Une barre de masse $m$ et de longueur $l$ qui tourne autour de son centre, qui coïncide avec le centre de masse :
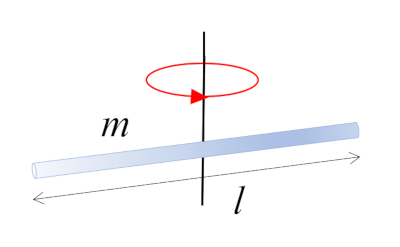
ID:(10962, 0)
Cylindre qui tourne autour de l'axe $\parallel$
Image 
Considérons une rotation d'un cylindre de masse $m$ et de rayon $r$ autour de l'axe du cylindre, où le centre de masse (CM) se situe à mi-hauteur :
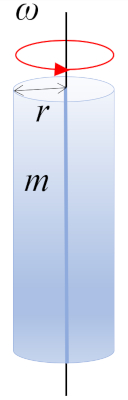
ID:(10964, 0)
Cylindre qui tourne autour de l'axe $\perp$
Image 
Dans cette situation, un cylindre avec une masse $m$, un rayon $r$ et une hauteur $h$ tourne autour d'un axe perpendiculaire à son propre axe. Cet axe passe par le milieu de la longueur du cylindre, où se trouve le centre de masse (CM) :
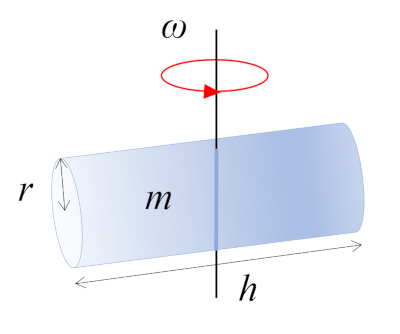
ID:(10965, 0)
Moment d'inertie d'un parallélépipède régulier
Image 
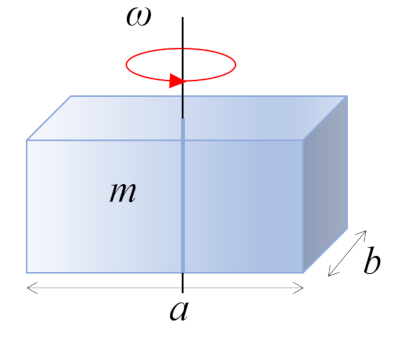
Un parallélépipède rectangle de masse $m$ et de côtés $a$ et $b$, perpendiculaire à l'axe de rotation, tourne autour de son centre de masse, qui se trouve au centre géométrique du corps:
ID:(10973, 0)
Parallélépipède droit
Image 
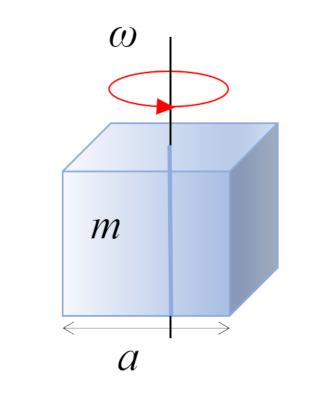
Dans le cas d'un parallélépipède rectangle avec une masse $m$ et un côté $a$, le centre de masse se situe au centre géométrique :
ID:(10963, 0)
Modèle
Top 
Paramètres
Variables
Calculs
Calculs
Calculs
Équations
$ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$
I_CM = 2 * m * r_e ^ 2 / 5
$ I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2)$
I_CM = m * ( a ^ 2 + b ^ 2 ) / 12
$ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$
I_CM = m * ( h ^ 2 + 3 * r_c ^ 2 ) / 12
$ I_{CM} =\displaystyle\frac{1}{6} m a ^2$
I_CM = m * a ^2/6
$ I_{CM} =\displaystyle\frac{1}{12} m l ^2$
I_CM = m * l ^ 2 / 12
$ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$
I_CM = m * r_c ^2/2
$ K_r =\displaystyle\frac{1}{2} I \omega ^2$
K_r = I * omega ^2/2
ID:(15606, 0)
Moment d'inertie de la barre de longueur $l$ axe $\perp$
Équation 
Le moment d'inertie d'une barre en rotation autour d'un axe perpendiculaire ($\perp$) passant par le centre est obtenu en divisant le corps en petits volumes et en les additionnant :
ce qui aboutit à
.
ID:(4432, 0)
Moment d'inertie du cylindre, axe $\parallel$
Équation 
Le moment d'inertie d'un cylindre en rotation autour d'un axe parallèle ($\parallel$) à son axe central est obtenu en segmentant le corps en petits volumes et en les additionnant :
ce qui aboutit à
.
ID:(4434, 0)
Moment d'inertie du cylindre, axe $\perp$
Équation 
Le moment d'inertie d'un cylindre en rotation autour d'un axe perpendiculaire ($\perp$) passant par le centre est obtenu en divisant le corps en petits volumes et en les additionnant :
ce qui aboutit à
.
ID:(4435, 0)
Moment d'inertie d'un parallélépipède rectangle
Équation 
Le moment d'inertie d'un parallélépipède en rotation autour d'un axe passant par son centre est obtenu en divisant le corps en petits volumes et en les additionnant :
ce qui aboutit à
.
ID:(4433, 0)
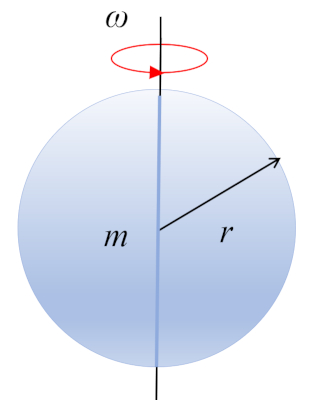
Moment d'inertie d'une sphère
Équation 
Le moment d'inertie d'une sphère en rotation autour d'un axe passant par son centre est obtenu en segmentant le corps en petits volumes et en les additionnant :
ce qui donne comme résultat :
.
ID:(4436, 0)
Énergie cinétique de rotation
Équation 
Dans le cas de l'étude de la translation, la définition de l'énergie
| $ \Delta W = T \Delta\theta $ |
est appliquée à la deuxième loi de Newton
| $ T = I \alpha $ |
ce qui conduit à l'expression
L'énergie nécessaire pour qu'un objet passe de la vitesse angulaire $\omega_1$ à la vitesse angulaire $\omega_2$ peut être calculée à l'aide de la définition
| $ \Delta W = T \Delta\theta $ |
Avec la deuxième loi de Newton, nous pouvons réécrire cette expression comme
$\Delta W=I \alpha \Delta\theta=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta$
En utilisant la définition de la vitesse angulaire
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
nous obtenons
$\Delta W=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta=I,\omega,\Delta\omega$
La différence entre les vitesses angulaires est
$\Delta\omega=\omega_2-\omega_1$
D'autre part, la vitesse angulaire elle-même peut être approximée par la vitesse angulaire moyenne
$\omega=\displaystyle\frac{\omega_1+\omega_2}{2}$
En utilisant ces deux expressions, nous obtenons l'équation
$\Delta W=I \omega \Delta \omega=I(\omega_2-\omega_1)\displaystyle\frac{(\omega_1+\omega_2)}{2}=\displaystyle\frac{I}{2}(\omega_2^2-\omega_1^2)$
Ainsi, l'énergie varie selon
$\Delta W=\displaystyle\frac{I}{2}\omega_2^2-\displaystyle\frac{I}{2}\omega_1^2$
Nous pouvons utiliser cela pour définir l'énergie cinétique
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
ID:(3255, 0)