Energía cinética de rotación
Storyboard 
La energía cinética de rotación es una función de la velocidad angular alcanzada mediante la aplicación de un torque durante un cierto tiempo mientras se recorre un ángulo dado.
Por lo tanto, la energía cinética rotacional es proporcional al momento de inercia del objeto y al cuadrado de la velocidad angular.
ID:(1417, 0)
Barra que rota en torno a un eje $\perp$
Imagen 
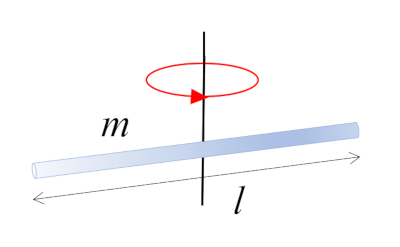
Una barra de masa $m$ y longitud $l$ que gira alrededor de su centro, que coincide con el centro de masa:
ID:(10962, 0)
Cilindro que rota en torno a eje $\parallel$
Imagen 
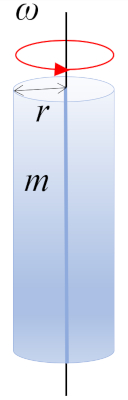
Una rotación de un cilindro con masa $m$ y radio $r$ alrededor del eje del cilindro, donde el centro de masa (CM) se encuentra a media altura:
ID:(10964, 0)
Cilindro que rota en torno a eje $\perp$
Imagen 
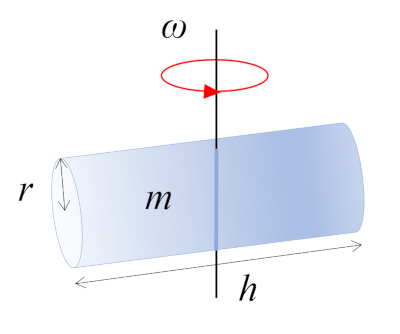
En esta situación, un cilindro con masa $m$, radio $r$ y altura $h$ está girando alrededor de un eje que es perpendicular a su propio eje. Este eje pasa por el punto medio de la longitud del cilindro, donde se localiza el centro de masa (CM):
ID:(10965, 0)
Momento de inercia de paralelepípedo regular
Imagen 
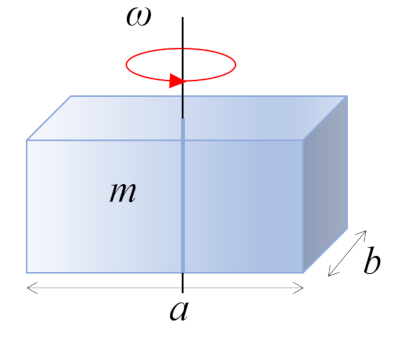
Un paralelepípedo rectángulo con masa $m$, lados $a$ y $b$, y perpendicular al eje de rotación, está girando alrededor de su centro de masa, que se encuentra en el centro geométrico del cuerpo:
ID:(10973, 0)
Paralelepípedo recto
Imagen 
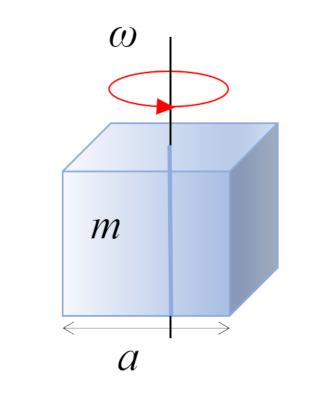
Para un paralelepípedo recto con masa $m$ y lado $a$, el centro de masa se encuentra en el centro geométrico:
ID:(10963, 0)
Modelo
Top 
Parámetros
Variables
Cálculos
Cálculos
Cálculos
Ecuaciones
$ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$
I_CM = 2 * m * r_e ^ 2 / 5
$ I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2)$
I_CM = m * ( a ^ 2 + b ^ 2 ) / 12
$ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$
I_CM = m * ( h ^ 2 + 3 * r_c ^ 2 ) / 12
$ I_{CM} =\displaystyle\frac{1}{6} m a ^2$
I_CM = m * a ^2/6
$ I_{CM} =\displaystyle\frac{1}{12} m l ^2$
I_CM = m * l ^ 2 / 12
$ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$
I_CM = m * r_c ^2/2
$ K_r =\displaystyle\frac{1}{2} I \omega ^2$
K_r = I * omega ^2/2
ID:(15606, 0)
Momento de inercia de barra de largo $l$ eje $\perp$
Ecuación 
El momento de inercia de una barra en rotación alrededor de un eje perpendicular ($\perp$) que pasa por el centro se obtiene al dividir el cuerpo en pequeños volúmenes y sumarlos:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
lo que resulta en
.
ID:(4432, 0)
Momento de inercia de cilindro, eje $\parallel$
Ecuación 
El momento de inercia de un cilindro que rota alrededor de un eje paralelo ($\parallel$) que pasa por el centro se calcula al dividir el cuerpo en pequeños volúmenes y sumarlos:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
lo que resulta en
.
ID:(4434, 0)
Momento de inercia de cilindro, eje $\perp$
Ecuación 
El momento de inercia de un cilindro que gira alrededor de un eje perpendicular ($\perp$) que pasa por el centro se calcula al dividir el cuerpo en pequeños volúmenes y sumarlos:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
lo que resulta en
.
ID:(4435, 0)
Momento de inercia de cubo recto
Ecuación 
El momento de inercia de un cubo que rota en torno a un eje que pasa por el centro se obtiene segmentando el cuerpo en pequeños volúmenes sumando:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
resultando
ID:(10972, 0)
Momento de inercia de paralelepípedo recto
Ecuación 
El momento de inercia de un paralelepípedo en rotación alrededor de un eje que pasa por el centro se obtiene al dividir el cuerpo en pequeños volúmenes y luego sumarlos:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
esto da como resultado
.
ID:(4433, 0)
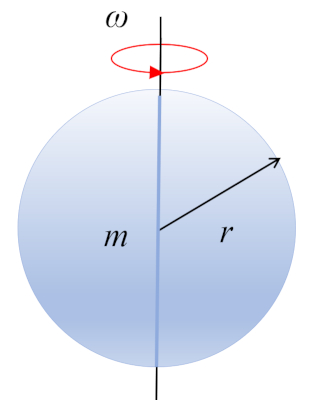
Momento de inercia de una esfera
Ecuación 
El momento de inercia de una esfera en rotación alrededor de un eje que atraviesa su centro se obtiene mediante la segmentación del cuerpo en pequeños volúmenes y sumando:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
lo que resulta en
.
ID:(4436, 0)
Energía cinética de rotación
Ecuación 
En el caso de estudio de la translación, la definición de la energía
| $ \Delta W = T \Delta\theta $ |
se aplica al segundo principio de Newton
| $ T = I \alpha $ |
lo que nos lleva a la expresión
La energía necesaria para que un objeto cambie su velocidad angular de $\omega_1$ a $\omega_2$ se puede calcular utilizando la definición
| $ \Delta W = T \Delta\theta $ |
Aplicando la segunda ley de Newton, esta expresión se puede reescribir como
$\Delta W=I \alpha \Delta\theta=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta$
Utilizando la definición de velocidad angular
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
obtenemos
$\Delta W=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta=I \omega \Delta\omega$
La diferencia en las velocidades angulares es
$\Delta\omega=\omega_2-\omega_1$
Por otro lado, la velocidad angular en sí se puede aproximar con la velocidad angular promedio
$\omega=\displaystyle\frac{\omega_1+\omega_2}{2}$
Utilizando ambas expresiones, obtenemos la ecuación
$\Delta W=I \omega \Delta \omega=I(\omega_2-\omega_1)\displaystyle\frac{(\omega_1+\omega_2)}{2}=\displaystyle\frac{I}{2}(\omega_2^2-\omega_1^2)$
Así, el cambio en la energía está dado por
$\Delta W=\displaystyle\frac{I}{2}\omega_2^2-\displaystyle\frac{I}{2}\omega_1^2$
Esto nos permite definir la energía cinética como
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
ID:(3255, 0)