Convertisseur travail-chaleur
Image 
La conversion du travail en énergie est étudiée en générant de la chaleur par frottement. Pour cela, on entoure un cylindre contenant de l'eau et un thermomètre d\'une bande métallique. En tournant la manivelle, la chaleur est générée par frottement, ce qui entraîne le réchauffement de l\'eau. Si l\'on mesure la force appliquée, le nombre de tours effectués et le rayon du cylindre, on peut estimer la distance parcourue, ce qui permet d\'estimer l\'énergie comme le produit de la force par la distance.

ID:(1884, 0)
Définition du chemin
Noter 
Pour n'importe quel chemin donné, il est possible de définir la force agissant en chaque point. De plus, si nous décomposons ce chemin en segments distincts représentés par des vecteurs $d\vec{x}$, nous pouvons calculer le produit scalaire entre eux pour déterminer l'énergie qui est consommée :
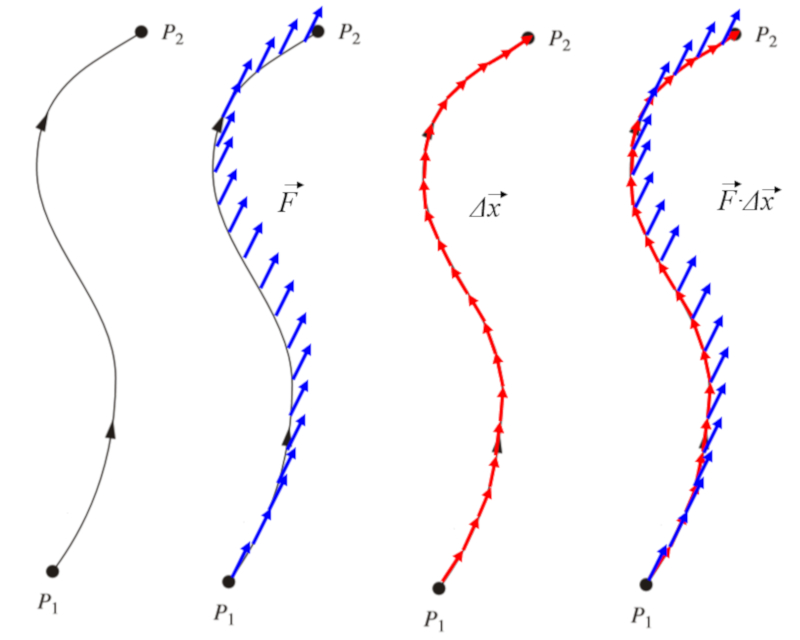
ID:(11514, 0)
