Working converter heat
Description 
The conversion of work into energy is studied by generating heat through friction. To do this, a metal band is wrapped around a cylinder containing water and a thermometer. By turning the crank, heat is generated through friction, leading to the heating of the water. If the applied force, the number of rotations, and the radius of the cylinder are measured, the distance traveled can be estimated, allowing for the estimation of energy as the product of force and distance.

ID:(1884, 0)
Path definition
Image 
For any given path, it's possible to define the force acting at each point. Furthermore, if we break down this path into distinct segments represented by vectors $d\vec{x}$, we can calculate the dot product between them to determine the energy being consumed:
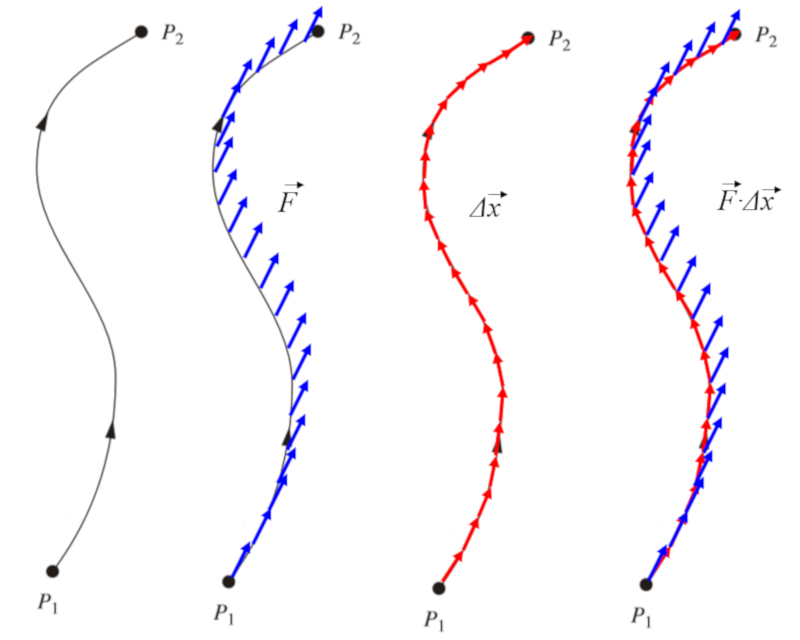
ID:(11514, 0)
