User:
Power
Storyboard 
An important limitation is the speed with which energy can be supplied to a system. This is particularly critical in the average that the system loses energy very quickly.
They introduce the concept of power that is defined as the energy supplied or lost per unit of time.
ID:(602, 0)
Variación del trabajo
Equation
La variación del trabajo en el tiempo se denomina la potencia. Por lo general es una limitante ya que indica la velocidad que es un sistema capaz de crear/absorber energía.
 $ \Delta W = W - W_0 $ |
ID:(4440, 0)
Potencia media
Equation
La potencia se define como la variación del trabajo en el tiempo lo que se expresa como
| $ P =\displaystyle\frac{ \Delta W }{ \Delta t }$ |
La potencia se define como la variación del trabajo
| $ \Delta W = W - W_0 $ |
en el tiempo
| $ \Delta t \equiv t - t_0 $ |
lo que se expresa como
| $ P =\displaystyle\frac{ \Delta W }{ \Delta t }$ |
La potencia es clave para entender las limitantes que tienen los sistemas para obtener o entregar energía limitando la forma como se comportan los objetos.
Los sistemas tienen un limite en la potencia que pueden generar (la energía que puede generar un sistema por unidad de tiempo) lo que limita su capacidad para cambiar la dinamica.
ID:(4439, 0)
Potencia instantánea
Equation
La potencia media calculada del trabajo
| $ P =\displaystyle\frac{ \Delta W }{ \Delta t }$ |
es una aproximación de la potencia real que tiende a distorsionarse en la medida que la energía fluctúe durante el intervalo de tiempo. Por ello se introduce el concepto de la potencia determinada en un tiempo muy pequeño. Se habla en este caso de un intervalo de tiempo infinitesimalmente pequeño.
| $P=\displaystyle\frac{dW}{dt}$ |
Si se considera la variación de la energía en el tiempo
$\Delta W = W(t+\Delta t)-W(t)$
\\n\\ny
$P_m=\displaystyle\frac{\Delta W}{\Delta t}=\displaystyle\frac{W(t+\Delta t)-W(t)}{\Delta t}\rightarrow \lim_{\Delta t\rightarrow 0}\displaystyle\frac{W(t+\Delta t)-W(t)}{\Delta t}=\displaystyle\frac{dW}{dt}=P$
Esta ultima expresión corresponde a la derivada de la función trabajo
| $P=\displaystyle\frac{dW}{dt}$ |
que a su vez es la pendiente de la representación gráfica de dicha función en el tiempo.
ID:(10612, 0)
Power needed in Flight
Image
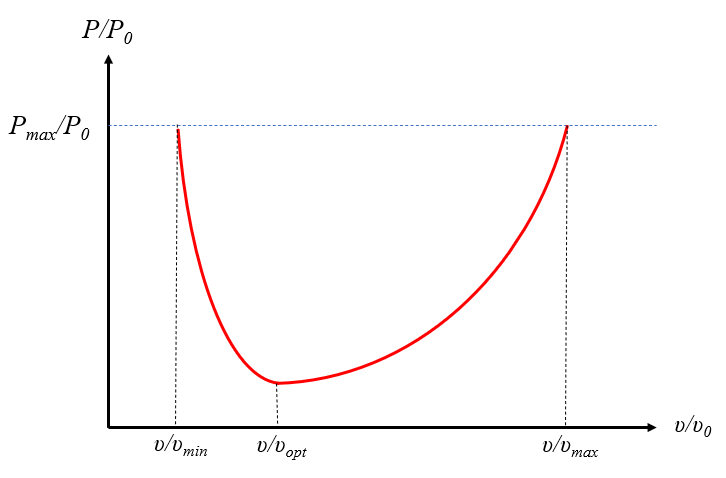
An example that illustrates how power is crucial to understanding the limitation of motion is the case of bird flight. The power curve as a function of flight velocity exhibits three main characteristics:
• It increases at low velocities due to the loss of lift and the phenomenon known as acoustic short-circuiting. In the latter situation, lift decreases because high pressure escapes from under the wings to the upper surface along the outer edge. To avoid this effect and save fuel, modern aircraft have winglets, which are short perpendicular extensions on the wings. This limitation implies that birds also require takeoff and landing distances; they cannot take off from a standstill or land without running.
• A minimum power point utilized by migratory birds for covering long distances with low energy consumption. This minimum depends on wing shape, meaning that only some birds have the capability for migration.
• A maximum power point occurs at high speeds, resulting in higher energy consumption for faster flight. Once again, wing shape is crucial to achieve high speeds, which characterizes birds of prey. Typically, bird wing designs are optimized for either hunting or migration, with only a few species utilizing both strategies.
ID:(51, 0)
0
Video
Video: Power