Usuario:
Potencia
Storyboard 
Un limitante importante es la velocidad con que se puede suministrar energía a un sistema. Esto es en particular critico en la media de que el sistema pierde energía en forma muy rápida.
Por ellos se introduce el concepto de potencia que se define como la energía suministrada o perdida por unidad de tiempo.
ID:(602, 0)
Variación del trabajo
Ecuación
La variación del trabajo en el tiempo se denomina la potencia. Por lo general es una limitante ya que indica la velocidad que es un sistema capaz de crear/absorber energía.
 $ \Delta W = W - W_0 $ |
ID:(4440, 0)
Potencia media
Ecuación
La potencia se define como la variación del trabajo en el tiempo lo que se expresa como
| $ P =\displaystyle\frac{ \Delta W }{ \Delta t }$ |
La potencia se define como la variación del trabajo
| $ \Delta W = W - W_0 $ |
en el tiempo
| $ \Delta t \equiv t - t_0 $ |
lo que se expresa como
| $ P =\displaystyle\frac{ \Delta W }{ \Delta t }$ |
La potencia es clave para entender las limitantes que tienen los sistemas para obtener o entregar energía limitando la forma como se comportan los objetos.
Los sistemas tienen un limite en la potencia que pueden generar (la energía que puede generar un sistema por unidad de tiempo) lo que limita su capacidad para cambiar la dinamica.
ID:(4439, 0)
Potencia instantánea
Ecuación
La potencia media calculada del trabajo
| $ P =\displaystyle\frac{ \Delta W }{ \Delta t }$ |
es una aproximación de la potencia real que tiende a distorsionarse en la medida que la energía fluctúe durante el intervalo de tiempo. Por ello se introduce el concepto de la potencia determinada en un tiempo muy pequeño. Se habla en este caso de un intervalo de tiempo infinitesimalmente pequeño.
| $P=\displaystyle\frac{dW}{dt}$ |
Si se considera la variación de la energía en el tiempo
$\Delta W = W(t+\Delta t)-W(t)$
\\n\\ny
$P_m=\displaystyle\frac{\Delta W}{\Delta t}=\displaystyle\frac{W(t+\Delta t)-W(t)}{\Delta t}\rightarrow \lim_{\Delta t\rightarrow 0}\displaystyle\frac{W(t+\Delta t)-W(t)}{\Delta t}=\displaystyle\frac{dW}{dt}=P$
Esta ultima expresión corresponde a la derivada de la función trabajo
| $P=\displaystyle\frac{dW}{dt}$ |
que a su vez es la pendiente de la representación gráfica de dicha función en el tiempo.
ID:(10612, 0)
Potencia necesaria en vuelo
Imagen
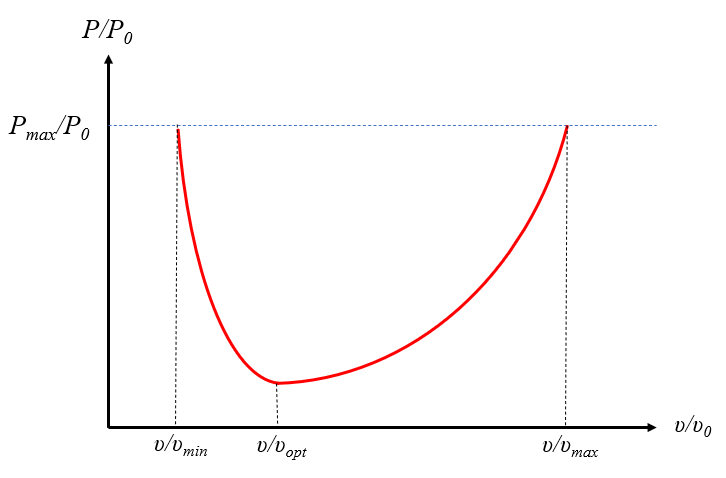
Un ejemplo que ilustra cómo la potencia es fundamental para comprender la limitación del movimiento es el caso del vuelo de las aves. La curva de potencia en función de la velocidad de vuelo exhibe tres características principales:
• Aumenta en velocidades bajas debido a la pérdida de sustentación y al fenómeno conocido como cortocircuito acústico. En esta última situación, la sustentación disminuye debido a la fuga de alta presión desde la parte inferior de las alas hacia la parte superior a lo largo de su borde exterior. Para evitar este efecto y ahorrar combustible, las aeronaves modernas cuentan con winglets, que son extensiones cortas perpendiculares en las alas. Esta limitación implica que también las aves requieren espacio para despegar y aterrizar; no pueden despegar desde el reposo o aterrizar sin correr.
• Un mínimo que es aprovechado por las aves migratorias para recorrer largas distancias con un bajo consumo de energía. Este mínimo depende de la forma del ala, lo que significa que solo algunas aves tienen la capacidad de migrar.
• Un máximo que se alcanza a altas velocidades, lo que resulta en un mayor consumo de energía para volar más rápido. Nuevamente, la forma de las alas es fundamental para lograr altas velocidades, lo que caracteriza a las aves rapaces. Por lo general, las aves presentan diseños de alas optimizados para la caza o la migración, con pocas especies que emplean ambas estrategias.
ID:(51, 0)
0
Video
Video: Potencia