Rotational kinetic energy
Storyboard 
The kinetic energy of rotation is a function of the angular velocity achieved through the application of torque over a given time while traversing a given angle.
Thus, rotational kinetic energy is proportional to the moment of inertia of the object and the square of the angular velocity.
ID:(1417, 0)
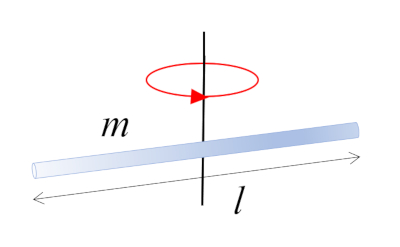
Bar that rotates around an axis $\perp$
Image 
A bar with mass $m$ and length $l$ rotating around its center, which coincides with the center of mass:
ID:(10962, 0)
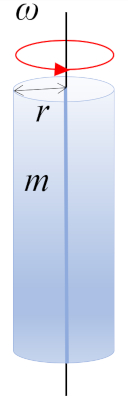
Cylinder rotating around axis $\parallel$
Image 
A rotation of a cylinder with mass $m$ and radius $r$ around the axis of the cylinder, where the center of mass (CM) is located at mid-height:
ID:(10964, 0)
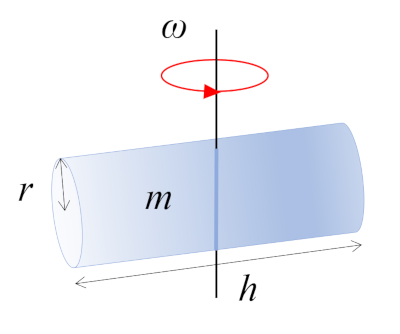
Cylinder that rotates about axis $\perp$
Image 
In this scenario, a cylinder with mass $m$, radius $r$, and height $h$ is rotating around an axis perpendicular to its own axis. This axis passes through the midpoint of the cylinder's length, where the center of mass (CM) is located:
ID:(10965, 0)
Regular parallelepiped moment of inertia
Image 
A straight rectangular parallelepiped with mass $m$ and sides $a$ and $b$, perpendicular to the axis of rotation, is rotating around its center of mass, which is located at the geometric center of the body:
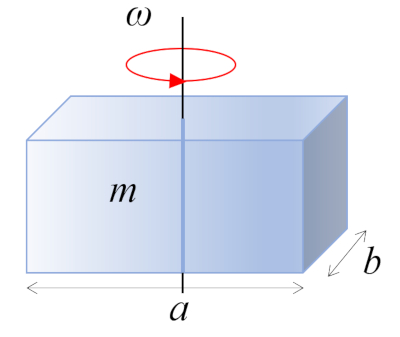
ID:(10973, 0)
Straight parallelepiped
Image 
In the case of a right rectangular parallelepiped with mass $m$ and side $a$, the center of mass is located at the geometric center:
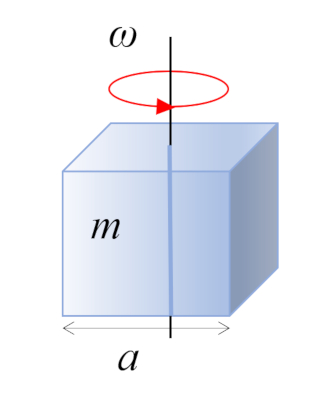
ID:(10963, 0)
Model
Top 
Parameters
Variables
Calculations
Calculations
Calculations
Equations
$ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$
I_CM = 2 * m * r_e ^ 2 / 5
$ I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2)$
I_CM = m * ( a ^ 2 + b ^ 2 ) / 12
$ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$
I_CM = m * ( h ^ 2 + 3 * r_c ^ 2 ) / 12
$ I_{CM} =\displaystyle\frac{1}{6} m a ^2$
I_CM = m * a ^2/6
$ I_{CM} =\displaystyle\frac{1}{12} m l ^2$
I_CM = m * l ^ 2 / 12
$ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$
I_CM = m * r_c ^2/2
$ K_r =\displaystyle\frac{1}{2} I \omega ^2$
K_r = I * omega ^2/2
ID:(15606, 0)
Moment of inertia of bar length $l$ axis $\perp$
Equation 
The moment of inertia of a rod rotating around a perpendicular ($\perp$) axis passing through the center is obtained by dividing the body into small volumes and summing them:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
resulting in
.
ID:(4432, 0)
Cylinder moment of inertia, axis $\parallel$
Equation 
The moment of inertia of a cylinder rotating around an axis parallel ($\parallel$) to its central axis is obtained by segmenting the body into small volumes and summing them:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
resulting in
.
ID:(4434, 0)
Cylinder moment of inertia, axis $\perp$
Equation 
The moment of inertia of a cylinder rotating around a perpendicular ($\perp$) axis passing through the center is obtained by segmenting the body into small volumes and summing them:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
resulting in
.
ID:(4435, 0)
Momento de inercia de cubo recto
Equation 
El momento de inercia de un cubo que rota en torno a un eje que pasa por el centro se obtiene segmentando el cuerpo en pequeños volúmenes sumando:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
resultando
ID:(10972, 0)
Moment of inertia of a right parallelepiped
Equation 
The moment of inertia of a parallelepiped rotating around an axis passing through its center is obtained by partitioning the body into small volumes and summing them up:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
resulting in
.
ID:(4433, 0)
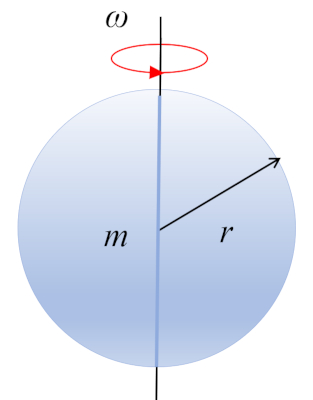
Moment of inertia of a sphere
Equation 
The moment of inertia of a sphere rotating around an axis passing through its center is obtained by segmenting the body into small volumes and summing:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
resulting in
.
ID:(4436, 0)
Kinetic Energy of Rotation
Equation 
In the case being studied of translational motion, the definition of energy
| $ \Delta W = T \Delta\theta $ |
is applied to Newton's second law
| $ T = I \alpha $ |
resulting in the expression
The energy required for an object to change its angular velocity from $\omega_1$ to $\omega_2$ can be calculated using the definition
| $ \Delta W = T \Delta\theta $ |
Applying Newton's second law, this expression can be rewritten as
$\Delta W=I \alpha \Delta\theta=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta$
Using the definition of angular velocity
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
we get
$\Delta W=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta=I \omega \Delta\omega$
The difference in angular velocities is
$\Delta\omega=\omega_2-\omega_1$
On the other hand, angular velocity itself can be approximated with the average angular velocity
$\omega=\displaystyle\frac{\omega_1+\omega_2}{2}$
Using both expressions, we obtain the equation
$\Delta W=I \omega \Delta \omega=I(\omega_2-\omega_1)\displaystyle\frac{(\omega_1+\omega_2)}{2}=\displaystyle\frac{I}{2}(\omega_2^2-\omega_1^2)$
Thus, the change in energy is given by
$\Delta W=\displaystyle\frac{I}{2}\omega_2^2-\displaystyle\frac{I}{2}\omega_1^2$
This allows us to define kinetic energy as
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
ID:(3255, 0)