Energia cinética rotacional
Storyboard 
A energia cinética de rotação é uma função da velocidade angular alcançada através da aplicação de um torque durante um certo tempo, enquanto percorre um determinado ângulo.
Assim, a energia cinética de rotação é proporcional ao momento de inércia do objeto e ao quadrado da velocidade angular.
ID:(1417, 0)
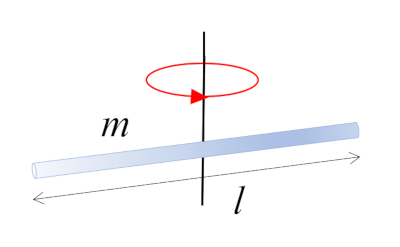
Barra que gira em torno de um eixo $\perp$
Imagem 
Uma barra com massa $m$ e comprimento $l$ que gira em torno do seu centro, que coincide com o centro de massa:
ID:(10962, 0)
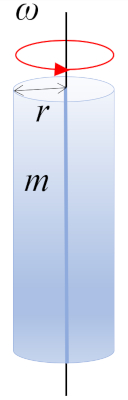
Cilindro que gira em torno do eixo $\parallel$
Imagem 
Uma rotação de um cilindro com massa $m$ e raio $r$ em torno do eixo do cilindro, onde o centro de massa (CM) está localizado a meia altura:
ID:(10964, 0)
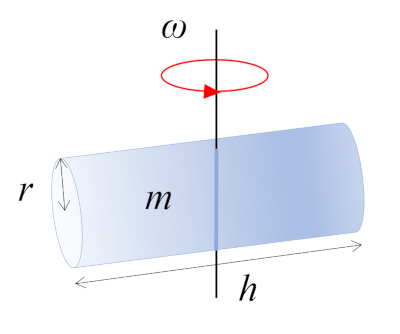
Cilindro que gira em torno do eixo $\perp$
Imagem 
Neste cenário, um cilindro com massa $m$, raio $r$ e altura $h$ está girando em torno de um eixo perpendicular ao seu próprio eixo. Esse eixo passa pelo ponto médio do comprimento do cilindro, onde se encontra o centro de massa (CM):
ID:(10965, 0)
Momento de inércia de um paralelepípedo regular
Imagem 
Um paralelepípedo reto com massa $m$ e lados $a$ e $b$, perpendicular ao eixo de rotação, está girando em torno de seu centro de massa, que se encontra no centro geométrico do corpo:
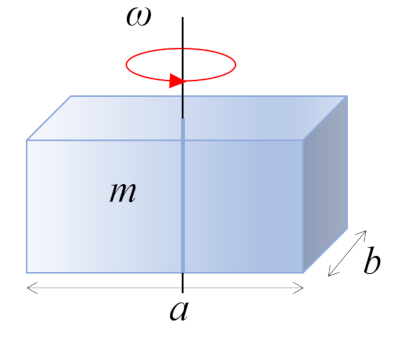
ID:(10973, 0)
Paralelepípedo direito
Imagem 
No caso de um paralelepípedo reto com massa $m$ e lado $a$, o centro de massa está localizado no centro geométrico:
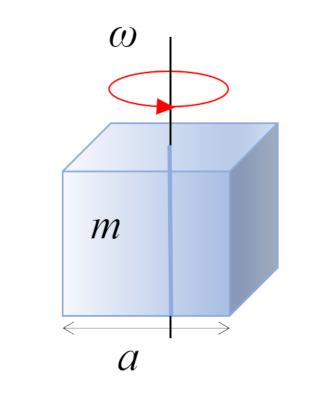
ID:(10963, 0)
Modelo
Top 
Parâmetros
Variáveis
Cálculos
Cálculos
Cálculos
Equações
$ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$
I_CM = 2 * m * r_e ^ 2 / 5
$ I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2)$
I_CM = m * ( a ^ 2 + b ^ 2 ) / 12
$ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$
I_CM = m * ( h ^ 2 + 3 * r_c ^ 2 ) / 12
$ I_{CM} =\displaystyle\frac{1}{6} m a ^2$
I_CM = m * a ^2/6
$ I_{CM} =\displaystyle\frac{1}{12} m l ^2$
I_CM = m * l ^ 2 / 12
$ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$
I_CM = m * r_c ^2/2
$ K_r =\displaystyle\frac{1}{2} I \omega ^2$
K_r = I * omega ^2/2
ID:(15606, 0)
Momento de inércia da barra de comprimento $l$ eixo $\perp$
Equação 
O momento de inércia de uma barra que está em rotação em torno de um eixo perpendicular ($\perp$) que passa pelo centro é obtido ao dividir o corpo em pequenos volumes e somá-los:
resultando em
.
ID:(4432, 0)
Momento de inércia do cilindro, eixo $\parallel$
Equação 
O momento de inércia de um cilindro que está em rotação em torno de um eixo paralelo ($\parallel$) que passa pelo centro é obtido ao dividir o corpo em pequenos volumes e somá-los:
resultando em
.
ID:(4434, 0)
Momento de inércia do cilindro, eixo $\perp$
Equação 
O momento de inércia de um cilindro que está em rotação em torno de um eixo perpendicular ($\perp$) que passa pelo centro é obtido ao dividir o corpo em pequenos volumes e somá-los:
resultando em
.
ID:(4435, 0)
Momento de inércia de um paralelepípedo reto
Equação 
O momento de inércia de um paralelepípedo que está em rotação em torno de um eixo que passa pelo centro é obtido ao dividir o corpo em pequenos volumes e somá-los:
resultando em
.
ID:(4433, 0)
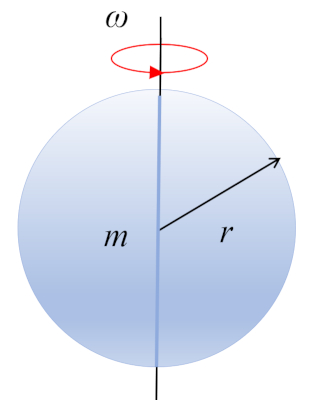
Momento de inércia de uma esfera
Equação 
O momento de inércia de uma esfera que gira em torno de um eixo que passa pelo centro é obtido pela segmentação do corpo em pequenos volumes e somando:
resultando em
.
ID:(4436, 0)
Energia cinética rotacional
Equação 
No caso em que se estuda a translação, a definição de energia
| $ \Delta W = T \Delta\theta $ |
é aplicada à segunda lei de Newton
| $ T = I \alpha $ |
resultando na expressão
A energia necessária para que um objeto passe da velocidade angular $\omega_1$ para a velocidade angular $\omega_2$ pode ser calculada usando a definição
| $ \Delta W = T \Delta\theta $ |
Com a segunda lei de Newton, podemos reescrever essa expressão como
$\Delta W=I \alpha \Delta\theta=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta$
Usando a definição de velocidade angular
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
obtemos
$\Delta W=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta=I \omega \Delta\omega$
A diferença entre as velocidades angulares é
$\Delta\omega=\omega_2-\omega_1$
Por outro lado, a própria velocidade angular pode ser aproximada pela velocidade angular média
$\omega=\displaystyle\frac{\omega_1+\omega_2}{2}$
Usando ambas as expressões, obtemos a equação
$\Delta W=I \omega \Delta \omega=I(\omega_2-\omega_1)\displaystyle\frac{(\omega_1+\omega_2)}{2}=\displaystyle\frac{I}{2}(\omega_2^2-\omega_1^2)$
Assim, a energia varia de acordo com
$\Delta W=\displaystyle\frac{I}{2}\omega_2^2-\displaystyle\frac{I}{2}\omega_1^2$
Podemos usar isso para definir a energia cinética
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
ID:(3255, 0)