Projection de champ électrique
Noter 
Le produit scalaire de deux vecteurs $\vec{a}$ et $\vec{b}$ peut être calculé en utilisant les modules des vecteurs et l'angle $\theta$ entre eux, comme suit :
Étant donné que le versor normal à la section ($\hat{n}$) a une magnitude égale à un, a projection de champ électrique ($E_n$) avec le champ électrique ($\vec{E}$), le versor normal à la section ($\hat{n}$) et a angle de champ électrique normal à la surface ($\alpha$) est :
ID:(15789, 0)
Géométrie du flux électrique
Citation 
Le champ n'est pas nécessairement orthogonal à la section à travers laquelle le flux est calculé. Il est donc nécessaire de calculer la composante du champ électrique qui est orthogonale à cette section :
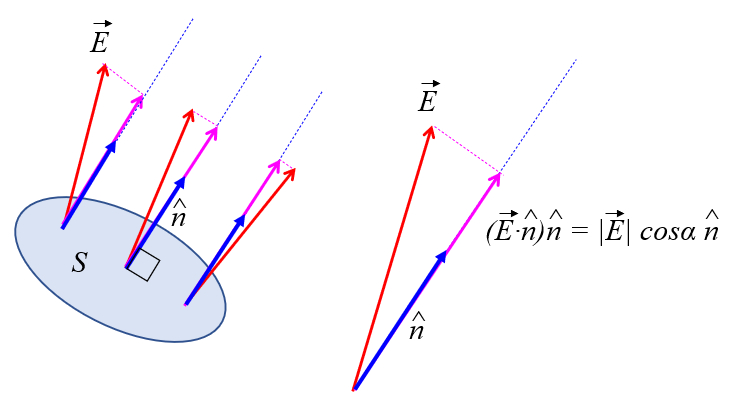
Comme le produit scalaire d'un vecteur avec un vecteur unitaire, dans ce cas, le vecteur unitaire qui définit l'orientation de la section, donne la projection de ce vecteur sur cette section, la composante à considérer est le produit scalaire ou le cosinus de l'angle a angle de champ électrique normal à la surface ($\alpha$) entre le champ électrique ($\vec{E}$) et le versor normal à la section ($\hat{n}$) :
ID:(11368, 0)
Écoulement à travers une section non plane et un champ variable
Exercer 
Comme la section n'est pas nécessairement plane, le vecteur normal peut varier dans son orientation. De même, le champ peut varier en direction et en magnitude sur la section. Par conséquent, la section peut être segmentée en petits éléments de surface qui, dans une première approximation, peuvent être considérés comme plans et où le champ ne varie ni en direction ni en magnitude :
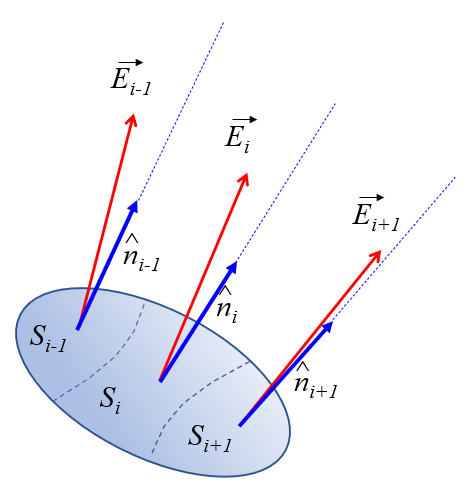
Par conséquent, le flux électrique ($\Phi$) est calculé en sommant, sur toute la section, la contribution de la composante normale du champ électrique à chaque élément de la section, calculée à partir de le champ électrique sur la surface i ($\vec{E}_i$) et le versor normal à la surface i ($\hat{n}_i$), et multipliée par a élément de surface i ($dS_i$) :
À la limite continue, la somme peut être remplacée par l'intégrale sur le élément surfacique ($dS$) du produit scalaire de le champ électrique ($\vec{E}$) et le versor normal à la section ($\hat{n}$) :
ID:(11373, 0)
Le flux électrique, en fonction de l'angle
Équation 
Le flux électrique ($\Phi$) est définie comme la composante normale du champ électrique, calculée à partir de le champ électrique sur la surface i ($\vec{E}_i$) et le versor normal à la surface i ($\hat{n}_i$), multipliée par a élément de surface i ($dS_i$) pour chaque élément $i$, puis sommée sur toute la section :
D'autre part, a projection de champ électrique ($E_n$) avec le champ électrique ($\vec{E}$), le versor normal à la section ($\hat{n}$) et a angle de champ électrique normal à la surface ($\alpha$) est égal à :
Par conséquent, avec a angle de champ électrique normal de la surface i ($\alpha_i$), nous avons :
Cela peut être étendu au cas continu en remplaçant la somme par une intégrale sur le élément surfacique ($dS$) du produit scalaire de le champ électrique ($\vec{E}$) et a angle de champ électrique normal à la surface ($\alpha$) :
ID:(15790, 0)
