mechanisms

Une mani re de comprendre la nature de la force entre deux charges est de consid rer que l'interaction est mod lis e par l' change de particules, qui dans ce cas sont des photons. Le nombre de ces messagers est proportionnel la charge qui les met ainsi qu' la probabilit qu'ils soient captur s par l'autre charge. Dans ce sens,

la force devrait tre proportionnelle au produit des deux charges.

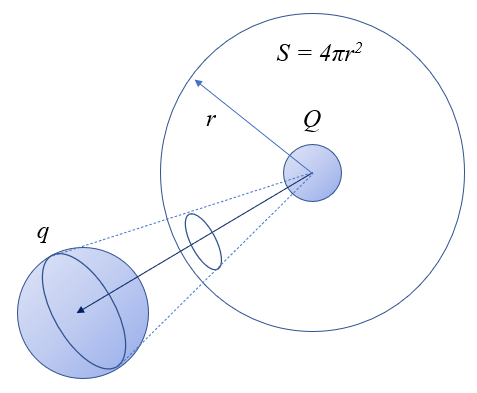
D'autre part, ces messagers sont mis dans toutes les directions, se distribuant sur une sph re imaginaire entourant la charge. La surface de cette sph re est $4\pi r^2$, o

r est le rayon, correspondant la distance entre les charges. Par cons quent,

la force devrait tre inversement proportionnelle au carr de la distance entre les charges, c'est- -dire inversement proportionnelle la surface de la sph re centr e sur l'autre charge.

Cette distribution peut tre repr sent e visuellement comme la surface autour d'une charge et le 'c ne' dans lequel les photons sont captur s par l'autre charge.

image

Ainsi, la force, en tant que quantit scalaire, prendrait la forme

$F \propto \displaystyle\frac{qQ}{4\pi r^2}$

La force entre les charges lectriques d pend de :

• Les magnitudes des charges, tant positive si les deux charges ont le m me signe et n gative si elles ont des signes oppos s.
• La magnitude de la force diminue avec le carr de la distance entre les charges.
• La direction de la force s'aligne le long de la ligne qui relie les deux charges.

image

Pour cette raison, Coulomb [1] a formul que a force à masse constante ($F$) est proportionnelle au produit des magnitudes des charges a charge d'essai ($q$) et a charge ($Q$), inversement proportionnelle au carr de a distance ($r$) qui les s pare, avec des constantes de proportionnalit a constante diélectrique ($\epsilon$) et a constante de champ électrique ($\epsilon_0$) :

equation=3212

La force de Coulomb agit dans la direction de a distance ($r$), qui peut tre repr sent e par le verson ($\hat{r}$). Par cons quent, l' quation pr c dente peut tre g n ralis e comme suit :

equation=15772

[1] "Premier M moire sur l lectricit et le Magn tisme", Charles-Augustin de Coulomb, Acad mie Royale des Sciences Paris, 1785.

A force ($\vec{F}$), g n r e entre deux charges repr sent es par a charge d'essai ($q$) et a charge ($Q$), qui se trouvent une distance de a distance ($r$), est calcul e en utilisant a constante de champ électrique ($\epsilon_0$) et a constante diélectrique ($\epsilon$). La direction est le long de a distance ($r$), ce qui peut tre repr sent par le verson ($\hat{r}$). Par cons quent, la loi est exprim e comme suit :

equation=15772

Si l'on consid re que a distance ($r$) est la distance entre a poste 1 ($\vec{s}_1$) et a poste 2 ($\vec{s}_2$), cela peut tre exprim comme :

equation=10390

et pour le verson ($\hat{r}$), en utilisant :

equation=10391

En associant a position ($\vec{r}$) avec a poste 2 ($\vec{s}_2$), a poste 1 ($\vec{s}_1$) avec a position d'une charge i ($\vec{u}_i$) et a charge ($Q$) avec a charge des ions i ($Q_i$), on peut conclure que le total de a force ($\vec{F}$) est :

equation=10392

model

A distance ($r$) repr sente la distance entre a poste 1 ($\vec{s}_1$) et a poste 2 ($\vec{s}_2$), qui peut tre exprim e comme suitxa0:

kyon

Le verson ($\hat{r}$) le long de la distance entre a poste 1 ($\vec{s}_1$) et a poste 2 ($\vec{s}_2$) peut tre calcul en utilisant la formule suivante :

kyon

La magnitude de a force à masse constante ($F$) g n r e entre deux charges, repr sent es par a charge d'essai ($q$) et a charge ($Q$), qui se trouvent une distance de a distance ($r$), est calcul e en utilisant a constante de champ électrique ($\epsilon_0$) et a constante diélectrique ($\epsilon$) de la mani re suivante :

kyon

A force ($\vec{F}$), g n r e entre deux charges repr sent es par a charge d'essai ($q$) et a charge ($Q$), qui se trouvent une distance de a distance ($r$), est calcul e en utilisant a constante de champ électrique ($\epsilon_0$) et a constante diélectrique ($\epsilon$). La direction est le long de a distance ($r$), ce qui peut tre repr sent par le verson ($\hat{r}$). Par cons quent, la loi s' crit comme suit :

kyon

A force ($\vec{F}$) sur a charge d'essai ($q$) A position ($\vec{r}$) d pendra de le nombre de charges ($N$), comptabilis es avec l'indice $i$ repr sent es par a charge des ions i ($Q_i$) situ es a position d'une charge i ($\vec{u}_i$). Avec les param tres a constante diélectrique ($\epsilon$) et a constante de champ électrique ($\epsilon_0$), cela peut s' crire comme suit :

kyon