Projeção de campo elétrico
Nota 
O produto escalar de dois vetores $\vec{a}$ e $\vec{b}$ pode ser calculado usando os módulos dos vetores e o ângulo $\theta$ entre eles, da seguinte forma:
Como o versor normal para seção ($\hat{n}$) tem uma magnitude igual a um, la projeção de campo elétrico ($E_n$) com o campo elétrico ($\vec{E}$), o versor normal para seção ($\hat{n}$) e la ângulo normal do campo elétrico da superfície ($\alpha$) é:
ID:(15789, 0)
Geometria de fluxo elétrico
Citar 
O campo não é necessariamente ortogonal à seção pela qual o fluxo está sendo calculado. Portanto, é necessário calcular a componente do campo elétrico que é ortogonal à seção:
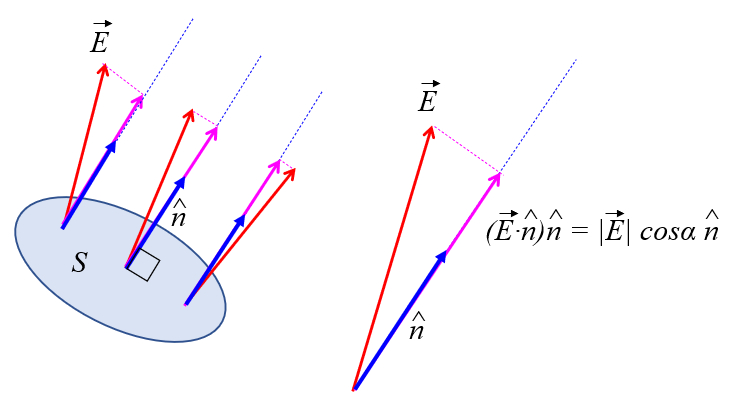
Como o produto escalar de um vetor com um vetor unitário, neste caso, o vetor unitário que define a orientação da seção, dá a projeção do vetor sobre esta seção, a componente a ser considerada é o produto escalar ou o cosseno do ângulo la ângulo normal do campo elétrico da superfície ($\alpha$) entre o campo elétrico ($\vec{E}$) e o versor normal para seção ($\hat{n}$):
ID:(11368, 0)
Fluxo através de seção não planar e campo variável
Exercício 
Como a seção não é necessariamente plana, o versor normal pode variar sua orientação. Da mesma forma, o campo pode variar em direção e magnitude sobre a seção. Portanto, a seção pode ser segmentada em pequenos elementos de superfície que, em uma primeira aproximação, podem ser considerados planos e onde o campo não varia nem em direção nem em magnitude:
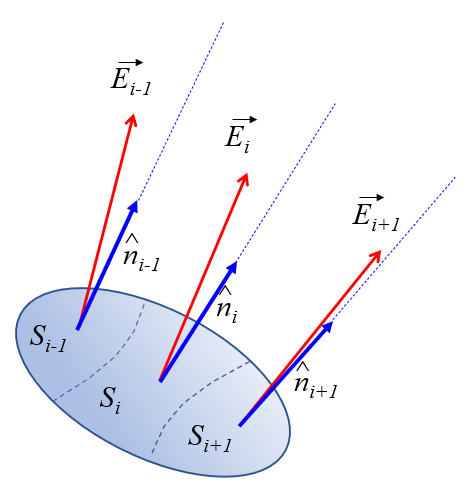
Portanto, o fluxo elétrico ($\Phi$) é calculado somando, sobre toda a seção, a contribuição da componente normal do campo elétrico para cada elemento da seção, calculada a partir de o campo elétrico na superfície i ($\vec{E}_i$) e o versor normal à superfície i ($\hat{n}_i$), e multiplicada por la elemento de superfície i ($dS_i$):
No limite contínuo, a soma pode ser substituída pela integral sobre o elemento de superfície ($dS$) do produto escalar de o campo elétrico ($\vec{E}$) e o versor normal para seção ($\hat{n}$):
ID:(11373, 0)
O fluxo elétrico, dependendo do ângulo
Equação 
O fluxo elétrico ($\Phi$) é definida como a componente normal do campo elétrico, calculada a partir de o campo elétrico na superfície i ($\vec{E}_i$) e o versor normal à superfície i ($\hat{n}_i$), multiplicada por la elemento de superfície i ($dS_i$) para cada elemento $i$, que é então somada sobre toda a seção:
Por outro lado, la projeção de campo elétrico ($E_n$) com o campo elétrico ($\vec{E}$), o versor normal para seção ($\hat{n}$) e la ângulo normal do campo elétrico da superfície ($\alpha$) é igual a:
Portanto, com la ângulo normal do campo elétrico da superfície i ($\alpha_i$) temos:
Isso pode ser estendido para o caso contínuo, substituindo a soma por uma integral sobre o elemento de superfície ($dS$) do produto escalar de o campo elétrico ($\vec{E}$) e la ângulo normal do campo elétrico da superfície ($\alpha$):
ID:(15790, 0)
