Elektrisches Strömungskonzept
Bild 
Der Fluss wird durch das elektrische Feld und den Abschnitt definiert, den die Feldlinien durchlaufen:

ID:(11366, 0)
Elektrische Feldprojektion
Notiz 
Das Skalarprodukt von zwei Vektoren $\vec{a}$ und $\vec{b}$ kann unter Verwendung der Beträge der Vektoren und des Winkels $\theta$ zwischen ihnen berechnet werden, wie folgt:
Da der Versor normal zum Abschnitt ($\hat{n}$) eine Magnitude von eins hat, ist die Elektrische Feldprojektion ($E_n$) mit der Elektrisches Feld ($\vec{E}$), der Versor normal zum Abschnitt ($\hat{n}$) und die Oberflächennormaler elektrischer Feldwinkel ($\alpha$):
ID:(15789, 0)
Elektrische Strömungsgeometrie
Zitat 
Das Feld ist nicht unbedingt orthogonal zur Fläche, durch die der Fluss berechnet wird. Daher ist es notwendig, die Komponente des elektrischen Feldes zu berechnen, die orthogonal zur Fläche ist:
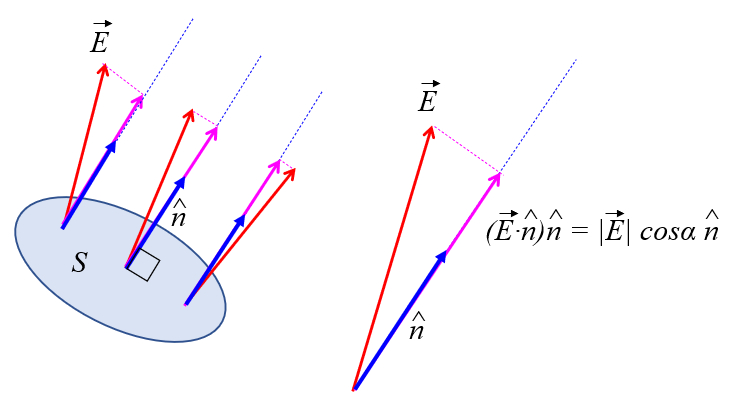
Da das Skalarprodukt eines Vektors mit einem Einheitsvektor, in diesem Fall der Einheitsvektor, der die Orientierung der Fläche definiert, die Projektion dieses Vektors auf diese Fläche ergibt, ist die zu betrachtende Komponente das Skalarprodukt oder der Kosinus des Winkels die Oberflächennormaler elektrischer Feldwinkel ($\alpha$) zwischen der Elektrisches Feld ($\vec{E}$) und der Versor normal zum Abschnitt ($\hat{n}$):
ID:(11368, 0)
Durchfluss durch nicht flachen Abschnitt und variables Feld
Übung 
Da der Abschnitt nicht unbedingt flach ist, kann der normale Versor seine Ausrichtung variieren. In ähnlicher Weise kann das Feld in Richtung und Größe des Abschnitts variieren. Aus diesem Grund kann der Abschnitt in kleine Oberflächenelemente unterteilt werden, die in erster Näherung als flach betrachtet werden können und in denen sich das Feld weder in Richtung noch in Größe ändert:
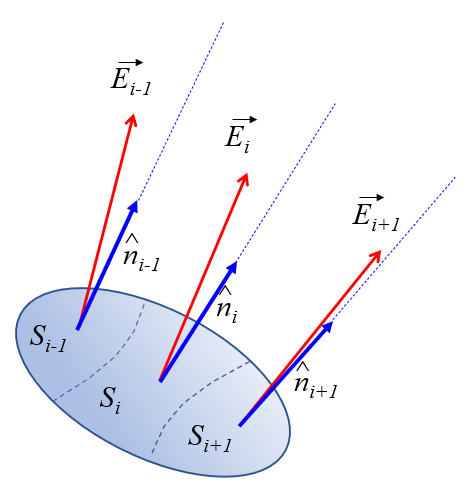
Daher wird der Elektrischer Fluss ($\Phi$) berechnet, indem über die gesamte Fläche die Beiträge der Normalkomponente des elektrischen Feldes zu jedem Flächenelement, berechnet aus der Elektrisches Oberflächenfeld i ($\vec{E}_i$) und der Versor normal zur Oberfläche i ($\hat{n}_i$), und multipliziert mit die Oberflächenelement i ($dS_i$), summiert werden:
Im kontinuierlichen Grenzfall kann die Summe durch das Integral über der Oberflächenelement ($dS$) des Skalarprodukts von der Elektrisches Feld ($\vec{E}$) und der Versor normal zum Abschnitt ($\hat{n}$) ersetzt werden:
ID:(11373, 0)
Der elektrische Fluss hängt vom Winkel ab
Gleichung 
Der Elektrischer Fluss ($\Phi$) wird als die Normalkomponente des elektrischen Feldes definiert, berechnet aus der Elektrisches Oberflächenfeld i ($\vec{E}_i$) und der Versor normal zur Oberfläche i ($\hat{n}_i$), multipliziert mit die Oberflächenelement i ($dS_i$) für jedes Element $i$, das dann über die gesamte Fläche summiert wird:
Andererseits ist die Elektrische Feldprojektion ($E_n$) mit der Elektrisches Feld ($\vec{E}$), der Versor normal zum Abschnitt ($\hat{n}$) und die Oberflächennormaler elektrischer Feldwinkel ($\alpha$) gleich:
Daher haben wir mit die Oberflächennormaler elektrischer Feldwinkel i ($\alpha_i$):
Dies kann auf den kontinuierlichen Fall erweitert werden, indem die Summe durch ein Integral über der Oberflächenelement ($dS$) des Skalarprodukts von der Elektrisches Feld ($\vec{E}$) und die Oberflächennormaler elektrischer Feldwinkel ($\alpha$) ersetzt wird:
ID:(15790, 0)
