Mischvorgänge in flachen Gewässern
Storyboard 
Mischmechanismen in flachen Gebieten werden von verschiedenen Arten von Wellen erzeugt. Dazu gehören interne Wellen, Oberflächenwellen, Wechselwirkungen zwischen Wellen und Strömungen, Gezeiten und Wellenbrechen an der Küste.
ID:(1629, 0)
Flache Mischmechanismen
Bild 
Para el caso en el borde costero en donde hay baja profundidad se tienen los siguientes mecanismos que contribuyen el mezclado de las aguas por efecto de:
• olas internas
adicionalmente existen contribuciones adicionales mediante
• mezcla por ola
• interacción de corriente con olas
• mezcla por mares
• mezcla por quiebre de olas en costa
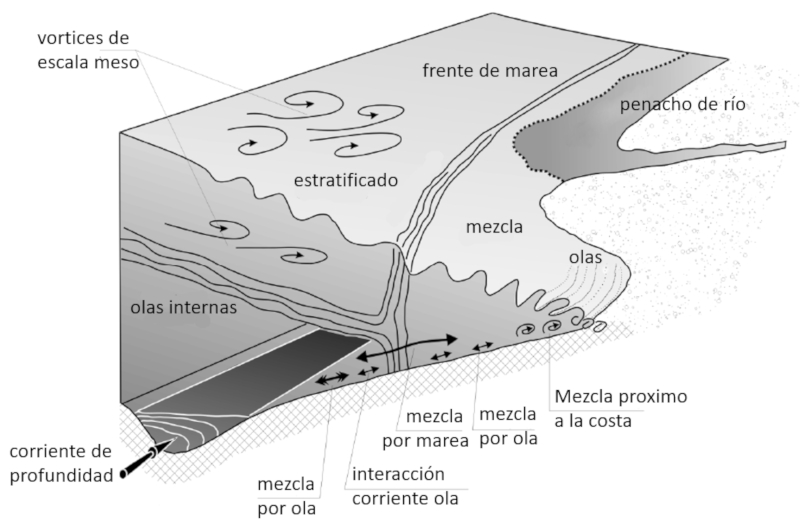
De Coastal Ocean Turbulence and Mixing, A.J. Souza, H. Burchard, C. Eden, C. Pattiaratchi, and H. van Haren, Coupled Coastal Wind, Wave and Current Dynamics (eds C. Mooers, P.Craig, N. Huang), Cambridge University Press (Cambridge, UK).
ID:(12196, 0)
Störungsgrößen
Bild 
Las perturbaciones se pueden ordenar en función de sus escalas de tiempo y dimensiones. El resultado se presenta en la siguiente grafica:
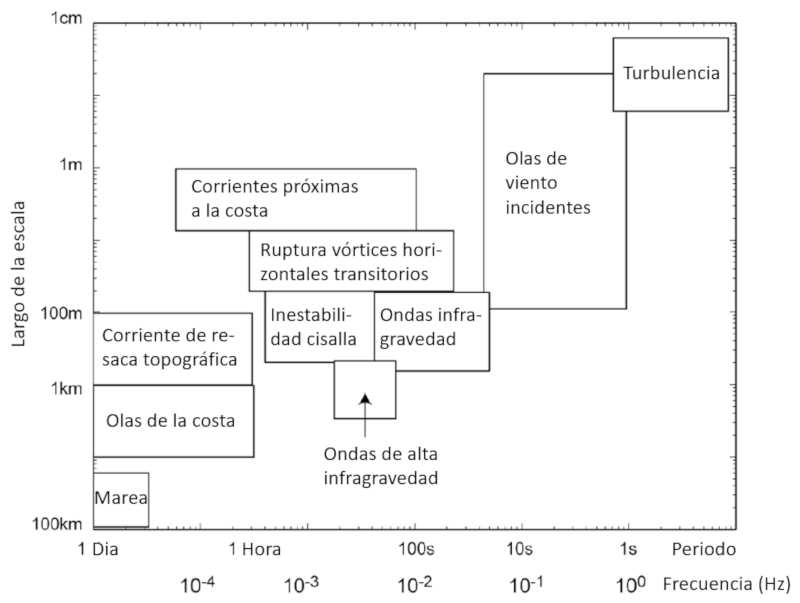
De Coastal Ocean Turbulence and Mixing, A.J. Souza, H. Burchard, C. Eden, C. Pattiaratchi, and H. van Haren, Coupled Coastal Wind, Wave and Current Dynamics (eds C. Mooers, P.Craig, N. Huang), Cambridge University Press (Cambridge, UK).
ID:(12200, 0)
Strouhal-Zahl als Funktion der Reynold-Zahl
Bild 
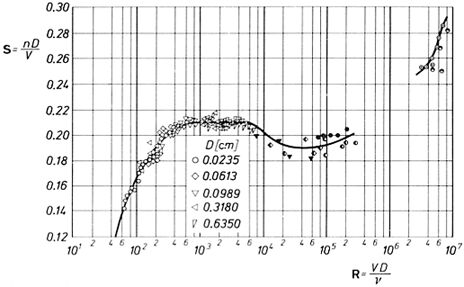
Der Strouhal-Zahl ($St$) steht empirisch in Beziehung zu der Reynolds Nummer ($Re$). Der Strouhal-Zahl ($St$) ist mit die Frequenz der Wirbelerzeugung ($\omega$), die Reibungsgeschwindigkeit ($U_d$) und die Gesamttiefe ($H$) verbunden:
| $ St \equiv \displaystyle\frac{ \omega H }{ U_d }$ |
Dies ermöglicht es, über der Reynolds Nummer ($Re$) die Häufigkeit zu schätzen, mit der sich die Konzentration der zu diffundierenden Komponenten austauschen kann. Es ist jedoch zu beachten, dass der Prozess abgebrochen werden kann, wenn die Häufigkeit geringer ist als die der Gezeiten.
ID:(12199, 0)
Kinematische Belastung
Beschreibung 
Wenn angenommen wird, dass es keinen Wind an der Oberfläche gibt, kann angenommen werden, dass dort keine Spannung existiert. Daher wird es nur Spannung des Wassers am Boden geben. Diese Spannung wird linear vom Boden zur Oberfläche abnehmen. Um das Modell zu vereinfachen, kann das Verhältnis zwischen die Tiefe ($z$) und die Gesamttiefe ($H$) verwendet werden, was uns einen dimensionslosen Faktor die Relative Tiefe ($\xi$) liefert. Die Kinematischer Stress ($\tau_x$) wird daher proportional sein zu
$\tau_x \propto 1-\xi$
Da die Kinematischer Stress ($\tau_x$) der Energiedichte geteilt durch die Dichte entspricht, muss der Wert am Boden proportional zum Quadrat der Geschwindigkeit am Boden sein. Dies wird im Modell mit die Reibungsgeschwindigkeit ($U_d$) beschrieben und bedeutet, dass
$\tau_x \propto U_d^2$
Schließlich gibt es den Effekt von die Rauigkeit ($k$) des Meeresbodens, d.h. das Verhältnis von der Unebenheit ($d$) und die Gesamttiefe ($H$). Dies bedeutet, dass die Kinematischer Stress ($\tau_x$) durch einen Faktor analog zur Tiefe korrigiert werden muss:
$\tau_x \propto \displaystyle\frac{1-\xi}{1-k}$
Daraus ergibt sich ein Modell der folgenden Form:
| $ \tau_x \equiv \displaystyle\frac{ U_d ^2}{1- k }(1- \xi )$ |
welches wie folgt grafisch dargestellt wird:
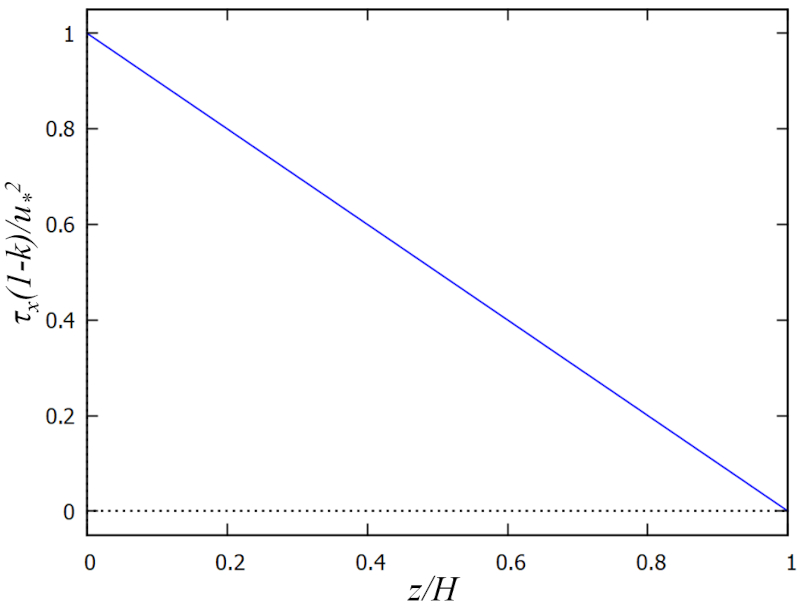
ID:(15630, 0)
Mischlänge
Beschreibung 
Die Mischlänge ($l$) entspricht der Größe der Wirbel. In der Nähe der Wand können diese nur so groß sein wie der Abstand zur Wand, was minimal ist. Je näher wir der Oberfläche kommen, desto größer können sie werden, sodass die Funktion an diesem Punkt ein Maximum erreichen sollte.
Um die Modellierung zu vereinfachen, kann das Verhältnis zwischen die Tiefe ($z$) und die Gesamttiefe ($H$) verwendet werden, was uns einen dimensionslosen Faktor die Relative Tiefe ($\xi$) liefert. Eine einfache Funktion, die dieser Beschreibung entspricht, ist:
$l \propto \xi\left(1-\displaystyle\frac{1}{2}\xi\right)$
Andererseits zeigt Prandtls Modell der Grenzschicht, dass diese eine Fraktion des Flusses mit einer Breite von die Gesamttiefe ($H$) und einem Anteil von die Karman-Konstante ($\kappa$) sind, sodass:
$l \propto \kappa H$
Schließlich müssen wir den Effekt der Rauheit auf die gleiche Weise wie beim kinematischen Stress korrigieren:
$l \propto \displaystyle\frac{\kappa H}{1-k}$
Daher kann die Mischlänge ($l$) wie folgt modelliert werden:
| $ l \equiv \displaystyle\frac{ \kappa H }{1 - k } \xi \left(1 - \displaystyle\frac{1}{2} \xi \right)$ |
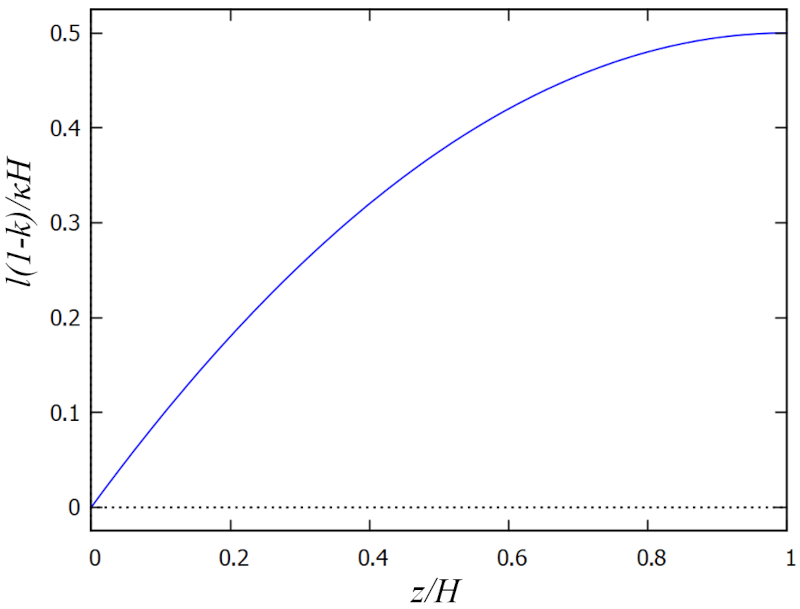
ID:(12201, 0)
Wirbelviskosität
Konzept 
Wenn Prandtl die Bildung von Wirbeln in der Nähe von Wänden modelliert, stellt er die Beziehung zwischen die Turbulente Viskosität ($A$), die Mischlänge ($l$) und dem Gradienten von der Geschwindigkeitsprofil ($u_z$) in die Tiefe ($z$) wie folgt her:
| $ A = l ^2\displaystyle\frac{\partial u_z }{\partial z }$ |
Auf der anderen Seite entspricht die typische viskose Kraft, die als Viskosität multipliziert mit der Kontaktfläche und dem Geschwindigkeitsgradienten modelliert wird, im Falle der Turbulenzen die Kinematischer Stress ($\tau_x$):
| $ \tau_x = A \displaystyle\frac{\partial u_z }{\partial z }$ |
Aus beiden Gleichungen ergibt sich die Beziehung:
| $ \tau_x = \displaystyle\frac{ A ^2 }{ l ^2 }$ |
Diese Beziehung ermöglicht die Berechnung von die Turbulente Viskosität ($A$) in Abhängigkeit von die Kinematischer Stress ($\tau_x$) und die Mischlänge ($l$), die in diesem Fall modelliert werden. So erhält man mit die Gesamttiefe ($H$), die Reibungsgeschwindigkeit ($U_d$), die Rauigkeit ($k$), die Relative Tiefe ($\xi$) und die Karman-Konstante ($\kappa$):
| $ A = \displaystyle\frac{ \kappa H U_d }{(1- k )^{3/2}} \xi \left(1- \displaystyle\frac{1}{2} \xi \right)\sqrt{1- \xi }$ |
die wie folgt dargestellt wird:
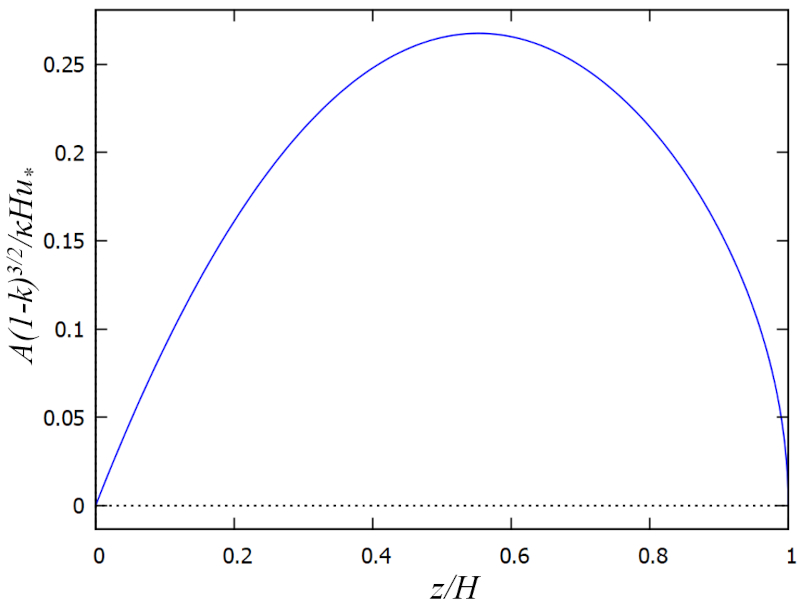
Das Ergebnis ist, dass die turbulente Viskosität in mittlerer Tiefe maximal ist und sowohl nahe dem Boden als auch nahe der Oberfläche auf minimale Werte abnimmt. Mit anderen Worten, in diesen Zonen sind das Mischen und der Impulsverlust geringer.
ID:(15624, 0)
Geschwindigkeitsprofil
Konzept 
Da die Kinematischer Stress ($\tau_x$) gleich die Turbulente Viskosität ($A$) und dem Gradienten von der Geschwindigkeitsprofil ($u_z$) in die Tiefe ($z$) ist, kann die Gleichung integriert werden, um das Geschwindigkeitsprofil zu erhalten:
$u_z = \displaystyle\int_d^z \frac{\tau_x}{A} , dz'$
Nach der Integration dieses Ausdrucks erhält man mit die Reibungsgeschwindigkeit ($U_d$), die Karman-Konstante ($\kappa$), die Rauigkeit ($k$) und die Relative Tiefe ($\xi$):
| $ u_z = \displaystyle\frac{ U_d }{ \kappa }\sqrt{1-k}\ln\left(\displaystyle\frac{ \xi }{ k }\right)$ |
was dem berühmten logarithmischen Gesetz entspricht, das von Prandtl und Schlichting entwickelt wurde.
Das Profil wird in der folgenden Grafik dargestellt:
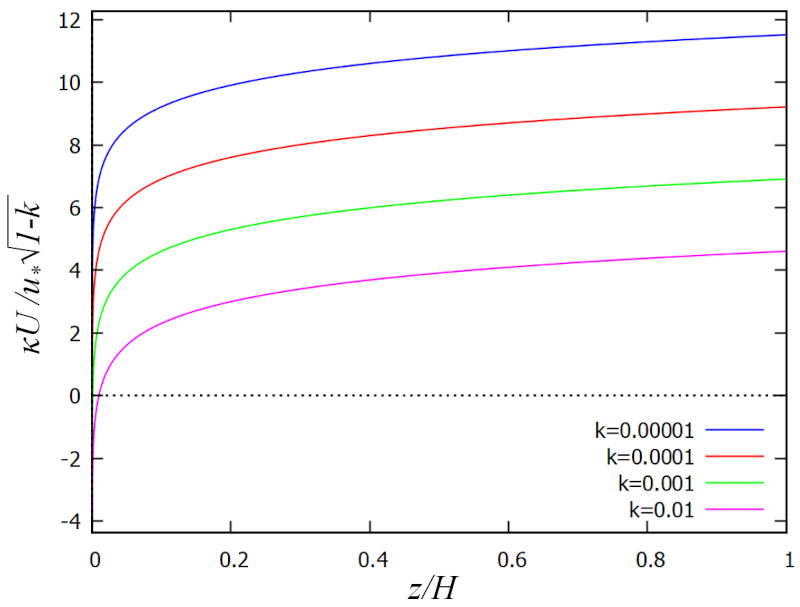
Das Profil ermöglicht es auch, der Velocidad en la superficie ($U$) mit die Reibungsgeschwindigkeit ($U_d$) in Abhängigkeit von die Rauigkeit ($k$) und die Karman-Konstante ($\kappa$) zu verknüpfen, was wiederum die Definition eines ERROR:9468 ermöglicht mit:
| $ U ^2 = \displaystyle\frac{ U_d ^2}{ C_D }$ |
und
| $ C_D = \displaystyle\frac{ \kappa ^2 }{(1- k ) \ln^2(1/ k )}$ |
ID:(15623, 0)
Sedimentkonzentration
Konzept 
Wenn wir das Verhalten des suspendierten Materials betrachten, werden zwei Hauptfaktoren deutlich. Erstens gibt es eine Tendenz zur Sedimentation mit einer Geschwindigkeit die Sedimentationsrate ($\omega_s$), die einen Fluss abhängig von der Concentración de sedimentos ($c_z$) generiert, ausgedrückt als:
$\omega_s c_z$
Auf der anderen Seite neigen Wirbel dazu, das Wasser zu mischen und eine Diffusion zu erzeugen, die Sedimente zur Oberfläche trägt. Dieser Fluss, repräsentiert durch die Turbulente Viskosität ($A$), wird durch den Gradienten von der Concentración de sedimentos ($c_z$) in die Tiefe ($z$) gegeben und ist gleich:
$A\displaystyle\frac{\partial c_z}{\partial z}$
Die Verteilung entsteht, wenn die Sedimente ein Gleichgewicht erreichen, bei dem der Sedimentationsfluss dem durch Wirbel erzeugten Diffusionsfluss zur Oberfläche entspricht. Durch Integration beider Terme der Gleichung mit der Erosionsrate ($E$) und der Unebenheit ($d$) erhalten wir die Verteilung:
$c_z=\displaystyle\frac{E}{\omega_s}e^{\displaystyle\int_d^z \omega_s/A dz'}$
Nach Verwendung des Ausdrucks für die Turbulente Viskosität ($A$) mit der Rouse Faktor ($R_s$), die Rauigkeit ($k$) und die Relative Tiefe ($\xi$) erhalten wir den Ausdruck:
| $ c_z = \displaystyle\frac{ E }{ \omega_s }\left(\displaystyle\frac{ k }{ \xi }\right)^{ R_s }$ |
der grafisch dargestellt werden kann als:
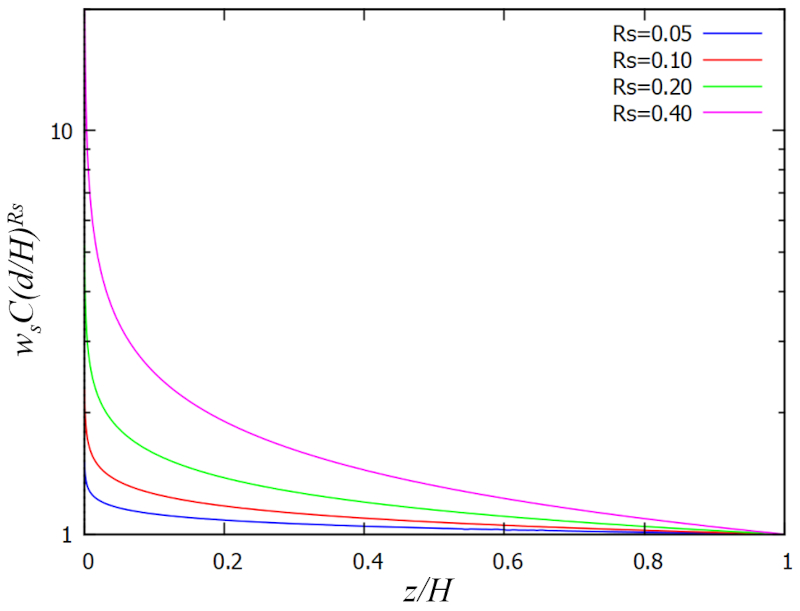
ID:(15631, 0)
Mischvorgänge in flachen Gewässern
Modell 
Mischmechanismen in flachen Gebieten werden von verschiedenen Arten von Wellen erzeugt. Dazu gehören interne Wellen, Oberflächenwellen, Wechselwirkungen zwischen Wellen und Strömungen, Gezeiten und Wellenbrechen an der Küste.
Variablen
Berechnungen
Berechnungen
Gleichungen
None
(ID 12182)
Genauso wie die Kinematischer Stress ($\tau_x$) mit die Turbulente Viskosität ($A$) und die Mischlänge ($l$) zusammenh ngt, ergibt sich:
| $ \tau_x = \displaystyle\frac{ A ^2 }{ l ^2 }$ |
Wenn die Karman-Konstante ($\kappa$), die Gesamttiefe ($H$) und die Rauigkeit ($k$) verwendet werden:
| $ l \equiv \displaystyle\frac{ \kappa H }{1 - k } \xi \left(1 - \displaystyle\frac{1}{2} \xi \right)$ |
und mit die Reibungsgeschwindigkeit ($U_d$):
| $ \tau_x \equiv \displaystyle\frac{ U_d ^2}{1- k }(1- \xi )$ |
ergibt sich:
| $ A = \displaystyle\frac{ \kappa H U_d }{(1- k )^{3/2}} \xi \left(1- \displaystyle\frac{1}{2} \xi \right)\sqrt{1- \xi }$ |
(ID 12185)
So wie die Kinematischer Stress ($\tau_x$) sich auf die Turbulente Viskosität ($A$), der Geschwindigkeitsprofil ($u_z$) und die Tiefe ($z$) bezieht, wird es durch
| $ \tau_x = A \displaystyle\frac{\partial u_z }{\partial z }$ |
definiert und kann von der Unebenheit ($d$) bis die Tiefe ($z$) integriert werden, um die Geschwindigkeit mit folgendem Ausdruck zu berechnen:
$u_z=\displaystyle\int_d^z\displaystyle\frac{\tau_x}{A}dz'$
Mit der Formulierung von die Turbulente Viskosität ($A$) in Bezug auf die Relative Tiefe ($\xi$) zusammen mit die Gesamttiefe ($H$), die Rauigkeit ($k$) und die Reibungsgeschwindigkeit ($U_d$), und unter Ber cksichtigung, dass
wird die folgende Geschwindigkeitsgleichung abgeleitet:
$u_z=\displaystyle\frac{U_d\sqrt{1-k}}{\kappa}(\ln(z/d) + \Phi(\xi,k))$
wo
$\Phi=2[\arctan(\lambda)-\arctan(\lambda_0)]-\ln\left(\displaystyle\frac{1+\lambda}{1+\lambda_0}\right)$
definiert wird mit
$\lambda=\sqrt{1-\xi}$
und
$\lambda=\sqrt{1-k}$
Da ber weite Teile der Tiefe
$\ln(z/d) \gg \Phi(\xi,k)$
kann das Geschwindigkeitsprofil vereinfacht werden zu
| $ u_z = \displaystyle\frac{ U_d }{ \kappa }\sqrt{1-k}\ln\left(\displaystyle\frac{ \xi }{ k }\right)$ |
(ID 12187)
Sedimente neigen dazu, mit eine Sedimentationsrate ($\omega_s$) zu Boden zu sinken, w hrend die Diffusion, die in diesem Fall dem durch Wirbel erzeugten Mischen entspricht, einen Fluss induziert, der gleich die Turbulente Viskosität ($A$) und dem Gradienten von der Concentración de sedimentos ($c_z$) in die Tiefe ($z$) ist, wie folgt:
$A\displaystyle\frac{\partial c_z}{\partial z}+\omega_s c_z= 0$
Die Integration dieses Ausdrucks ergibt:
$c_z = \displaystyle\frac{E}{\omega_s}e^{-\displaystyle\int_d^z \omega_s/A dz'}$
mit die Mischlänge ($l$):
| $ \tau_x = \displaystyle\frac{ A ^2 }{ l ^2 }$ |
haben wir:
$c_z=\displaystyle\frac{E}{\omega_s}e^{-\displaystyle\int_d^z \omega_s/l\sqrt{\tau_x} dz'}$
was zu folgendem Ergebnis f hrt:
$c_z=\displaystyle\frac{E}{\omega_s}\left(\displaystyle\frac{z}{d}\right)^{R_s}\Phi_c(\xi,k)$
mit der Rouse Faktor ($R_s$) und der Rouse-Nummer ($R_0$):
| $ R_s \equiv R_0 (1 - k )^{3/2}$ |
wo:
$\Phi=\left(\displaystyle\frac{1+\lambda}{1+\lambda_0}\right)^{2R_s}e^{2R_s[\arctan(\lambda)-\arctan(\lambda_0)]}$
mit:
$\lambda=\sqrt{1-\xi}$
und:
$\lambda=\sqrt{1-k}$
Da ber weite Teile der Tiefe:
$\Phi\sim 1$
haben wir die Konzentrationsverteilung:
| $ c_z = \displaystyle\frac{ E }{ \omega_s }\left(\displaystyle\frac{ k }{ \xi }\right)^{ R_s }$ |
(ID 12193)
Genauso wie die Turbulente Viskosität ($A$) mit die Mischlänge ($l$) verbunden ist, werden der Geschwindigkeitsprofil ($u_z$) und die Tiefe ($z$) wie folgt definiert:
| $ A = l ^2\displaystyle\frac{\partial u_z }{\partial z }$ |
und da die Kinematischer Stress ($\tau_x$) ist
| $ \tau_x = A \displaystyle\frac{\partial u_z }{\partial z }$ |
ergibt das Eliminieren des Gradienten
| $ \tau_x = \displaystyle\frac{ A ^2 }{ l ^2 }$ |
(ID 15633)
Beispiele
(ID 15614)
Para el caso en el borde costero en donde hay baja profundidad se tienen los siguientes mecanismos que contribuyen el mezclado de las aguas por efecto de:
• olas internas
adicionalmente existen contribuciones adicionales mediante
• mezcla por ola
• interacci n de corriente con olas
• mezcla por mares
• mezcla por quiebre de olas en costa

De Coastal Ocean Turbulence and Mixing, A.J. Souza, H. Burchard, C. Eden, C. Pattiaratchi, and H. van Haren, Coupled Coastal Wind, Wave and Current Dynamics (eds C. Mooers, P.Craig, N. Huang), Cambridge University Press (Cambridge, UK).
(ID 12196)
Las perturbaciones se pueden ordenar en funci n de sus escalas de tiempo y dimensiones. El resultado se presenta en la siguiente grafica:

De Coastal Ocean Turbulence and Mixing, A.J. Souza, H. Burchard, C. Eden, C. Pattiaratchi, and H. van Haren, Coupled Coastal Wind, Wave and Current Dynamics (eds C. Mooers, P.Craig, N. Huang), Cambridge University Press (Cambridge, UK).
(ID 12200)
Der Strouhal-Zahl ($St$) steht empirisch in Beziehung zu der Reynolds Nummer ($Re$). Der Strouhal-Zahl ($St$) ist mit die Frequenz der Wirbelerzeugung ($\omega$), die Reibungsgeschwindigkeit ($U_d$) und die Gesamttiefe ($H$) verbunden:
| $ St \equiv \displaystyle\frac{ \omega H }{ U_d }$ |
Dies erm glicht es, ber der Reynolds Nummer ($Re$) die H ufigkeit zu sch tzen, mit der sich die Konzentration der zu diffundierenden Komponenten austauschen kann. Es ist jedoch zu beachten, dass der Prozess abgebrochen werden kann, wenn die H ufigkeit geringer ist als die der Gezeiten.

(ID 12199)
Wenn angenommen wird, dass es keinen Wind an der Oberfl che gibt, kann angenommen werden, dass dort keine Spannung existiert. Daher wird es nur Spannung des Wassers am Boden geben. Diese Spannung wird linear vom Boden zur Oberfl che abnehmen. Um das Modell zu vereinfachen, kann das Verh ltnis zwischen die Tiefe ($z$) und die Gesamttiefe ($H$) verwendet werden, was uns einen dimensionslosen Faktor die Relative Tiefe ($\xi$) liefert. Die Kinematischer Stress ($\tau_x$) wird daher proportional sein zu
$\tau_x \propto 1-\xi$
Da die Kinematischer Stress ($\tau_x$) der Energiedichte geteilt durch die Dichte entspricht, muss der Wert am Boden proportional zum Quadrat der Geschwindigkeit am Boden sein. Dies wird im Modell mit die Reibungsgeschwindigkeit ($U_d$) beschrieben und bedeutet, dass
$\tau_x \propto U_d^2$
Schlie lich gibt es den Effekt von die Rauigkeit ($k$) des Meeresbodens, d.h. das Verh ltnis von der Unebenheit ($d$) und die Gesamttiefe ($H$). Dies bedeutet, dass die Kinematischer Stress ($\tau_x$) durch einen Faktor analog zur Tiefe korrigiert werden muss:
$\tau_x \propto \displaystyle\frac{1-\xi}{1-k}$
Daraus ergibt sich ein Modell der folgenden Form:
| $ \tau_x \equiv \displaystyle\frac{ U_d ^2}{1- k }(1- \xi )$ |
welches wie folgt grafisch dargestellt wird:

(ID 15630)
Die Mischlänge ($l$) entspricht der Gr e der Wirbel. In der N he der Wand k nnen diese nur so gro sein wie der Abstand zur Wand, was minimal ist. Je n her wir der Oberfl che kommen, desto gr er k nnen sie werden, sodass die Funktion an diesem Punkt ein Maximum erreichen sollte.
Um die Modellierung zu vereinfachen, kann das Verh ltnis zwischen die Tiefe ($z$) und die Gesamttiefe ($H$) verwendet werden, was uns einen dimensionslosen Faktor die Relative Tiefe ($\xi$) liefert. Eine einfache Funktion, die dieser Beschreibung entspricht, ist:
$l \propto \xi\left(1-\displaystyle\frac{1}{2}\xi\right)$
Andererseits zeigt Prandtls Modell der Grenzschicht, dass diese eine Fraktion des Flusses mit einer Breite von die Gesamttiefe ($H$) und einem Anteil von die Karman-Konstante ($\kappa$) sind, sodass:
$l \propto \kappa H$
Schlie lich m ssen wir den Effekt der Rauheit auf die gleiche Weise wie beim kinematischen Stress korrigieren:
$l \propto \displaystyle\frac{\kappa H}{1-k}$
Daher kann die Mischlänge ($l$) wie folgt modelliert werden:
| $ l \equiv \displaystyle\frac{ \kappa H }{1 - k } \xi \left(1 - \displaystyle\frac{1}{2} \xi \right)$ |

(ID 12201)
Wenn Prandtl die Bildung von Wirbeln in der N he von W nden modelliert, stellt er die Beziehung zwischen die Turbulente Viskosität ($A$), die Mischlänge ($l$) und dem Gradienten von der Geschwindigkeitsprofil ($u_z$) in die Tiefe ($z$) wie folgt her:
| $ A = l ^2\displaystyle\frac{\partial u_z }{\partial z }$ |
Auf der anderen Seite entspricht die typische viskose Kraft, die als Viskosit t multipliziert mit der Kontaktfl che und dem Geschwindigkeitsgradienten modelliert wird, im Falle der Turbulenzen die Kinematischer Stress ($\tau_x$):
| $ \tau_x = A \displaystyle\frac{\partial u_z }{\partial z }$ |
Aus beiden Gleichungen ergibt sich die Beziehung:
| $ \tau_x = \displaystyle\frac{ A ^2 }{ l ^2 }$ |
Diese Beziehung erm glicht die Berechnung von die Turbulente Viskosität ($A$) in Abh ngigkeit von die Kinematischer Stress ($\tau_x$) und die Mischlänge ($l$), die in diesem Fall modelliert werden. So erh lt man mit die Gesamttiefe ($H$), die Reibungsgeschwindigkeit ($U_d$), die Rauigkeit ($k$), die Relative Tiefe ($\xi$) und die Karman-Konstante ($\kappa$):
| $ A = \displaystyle\frac{ \kappa H U_d }{(1- k )^{3/2}} \xi \left(1- \displaystyle\frac{1}{2} \xi \right)\sqrt{1- \xi }$ |
die wie folgt dargestellt wird:

Das Ergebnis ist, dass die turbulente Viskosit t in mittlerer Tiefe maximal ist und sowohl nahe dem Boden als auch nahe der Oberfl che auf minimale Werte abnimmt. Mit anderen Worten, in diesen Zonen sind das Mischen und der Impulsverlust geringer.
(ID 15624)
Da die Kinematischer Stress ($\tau_x$) gleich die Turbulente Viskosität ($A$) und dem Gradienten von der Geschwindigkeitsprofil ($u_z$) in Bezug auf die Tiefe ($z$) ist, l sst sich die Gleichung integrieren, um das Geschwindigkeitsprofil zu erhalten:
$u_z = \displaystyle\int_d^z \frac{\tau_x}{A} dz'$
Nach der Integration unter Verwendung von die Reibungsgeschwindigkeit ($U_d$), die Karman-Konstante ($\kappa$), die Rauigkeit ($k$) und die Relative Tiefe ($\xi$) ergibt sich:
| $ u_z = \displaystyle\frac{ U_d }{ \kappa }\sqrt{1-k}\ln\left(\displaystyle\frac{ \xi }{ k }\right)$ |
Diese Gleichung entspricht dem bekannten logarithmischen Gesetz des Geschwindigkeitsprofils nach Prandtl und Schlichting.
Das Profil ist in der folgenden Grafik dargestellt:

Das Profil erm glicht auch eine Beziehung zwischen der Velocidad en la superficie ($U$) und die Reibungsgeschwindigkeit ($U_d$) in Abh ngigkeit von die Widerstandsbeiwert ($C_D$):
| $ U ^2 = \displaystyle\frac{ U_d ^2}{ C_D }$ |
Au erdem l sst sich die Widerstandsbeiwert ($C_D$) aus die Rauigkeit ($k$) und die Karman-Konstante ($\kappa$) absch tzen:
| $ C_D = \displaystyle\frac{ \kappa ^2 }{(1- k ) \ln^2(1/ k )}$ |
(ID 15623)
Wenn wir das Verhalten des suspendierten Materials betrachten, werden zwei Hauptfaktoren deutlich. Erstens gibt es eine Tendenz zur Sedimentation mit einer Geschwindigkeit die Sedimentationsrate ($\omega_s$), die einen Fluss abh ngig von der Concentración de sedimentos ($c_z$) generiert, ausgedr ckt als:
$\omega_s c_z$
Auf der anderen Seite neigen Wirbel dazu, das Wasser zu mischen und eine Diffusion zu erzeugen, die Sedimente zur Oberfl che tr gt. Dieser Fluss, repr sentiert durch die Turbulente Viskosität ($A$), wird durch den Gradienten von der Concentración de sedimentos ($c_z$) in die Tiefe ($z$) gegeben und ist gleich:
$A\displaystyle\frac{\partial c_z}{\partial z}$
Die Verteilung entsteht, wenn die Sedimente ein Gleichgewicht erreichen, bei dem der Sedimentationsfluss dem durch Wirbel erzeugten Diffusionsfluss zur Oberfl che entspricht. Durch Integration beider Terme der Gleichung mit der Erosionsrate ($E$) und der Unebenheit ($d$) erhalten wir die Verteilung:
$c_z=\displaystyle\frac{E}{\omega_s}e^{\displaystyle\int_d^z \omega_s/A dz'}$
Nach Verwendung des Ausdrucks f r die Turbulente Viskosität ($A$) mit der Rouse Faktor ($R_s$), die Rauigkeit ($k$) und die Relative Tiefe ($\xi$) erhalten wir den Ausdruck:
| $ c_z = \displaystyle\frac{ E }{ \omega_s }\left(\displaystyle\frac{ k }{ \xi }\right)^{ R_s }$ |
der grafisch dargestellt werden kann als:

(ID 15631)
(ID 15618)
ID:(1629, 0)
