Druyd:Knowledge

Uso de Lentes

Storyboard

ID:(292, 0)

Definir la geometría del lente optico

Definición

Finalmente podemos escoger el tipo de curvatura y si se asume que el anteojo tendrá un grosor d podemos calcular el radio correspondiente.

Para simplificar el calculo consideraremos que la curvatura por ambos es igual. El tipo de curvatura se puede concluir simplemente por el tipo de patología.

ID:(533, 0)

Geometría del lente

Imagen

Corrección con Lentes

Lentes

ID:(1864, 0)

Error de ojo y lente biconvexo

Nota

Hipermetropía

ID:(1862, 0)

Error de ojo y lente biconcavo

Cita

Miopía

ID:(1863, 0)

Multiples lentes

Ejercicio

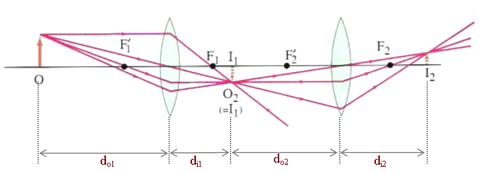
Cuando se acoplan dos lentes con sus respectivos focos, el primer lente genera una imagen que funciona como objeto para el segundo lente que a su vez genera una imagen de una imagen:

ID:(9465, 0)

Situación Lente Concavo-Convexo

Ecuación

Lente Convexo-Concavo grueso

ID:(1860, 0)

Situación Lente Convexo-Cóncavo

Script

Lente Concavo-Convexo grueso

ID:(1859, 0)

Diseño lente biconvexo

Variable

Lente Bi-Convexo grueso

ID:(1857, 0)

Situación Lente Biconcavo

Audio

Lente Bi-Concavo grueso

ID:(1858, 0)

Uso de Lentes

Descripción

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

$d$

Ancho del lente

$D$

Dioptria

1/m

$s_b$

s_b

Distancia Cristalino-retina

$s_{lc}$

s_lc

Distancia de la imagen del lente cóncavo

$s_o$

s_o

Distancia del objeto al lente cóncavo

$D$

Distancia Lente Óptico-Cristalino

$s_i$

s_i

Distancia Lente Óptico-Imagen intermedia

$s_o$

s_o

Distancia Objeto-Lente Óptico

$f_c$

f_c

Foco del Cristalino

$f_{ccd}$

f_ccd

Foco del lente bi-cóncavo grueso

$f_{csd}$

f_csd

Foco del lente bi-cóncavo simétrico

$f_{vvd}$

f_vvd

Foco del lente bi-convexo grueso

$f_{vsd}$

f_vsd

Foco del lente bi-convexo simétrico

$f_{lc}$

f_lc

Foco del lente cóncavo

$f_{lv}$

f_lv

Foco del lente convexo

$f_{vcd}$

f_vcd

Foco del lente convexo-cóncavo grueso

$n$

Indice de refracción de un medio

$R$

Radio del lente

$R_1$

R_1

Radio del lente en el lado de la fuente

$R_2$

R_2

Radio del lente en el lado de la imagen

$a_{lc}$

a_lc

Tamaño de la imagen en un lente cóncavo

$a_o$

a_o

Tamaño del objeto

$f_{cvs}$

f_cvs

Tiempo

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

$\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$

a_o / a_lc = s_o / s_lc

(ID 3346)

$\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$

1/ f_lc =1/ s_o +1/ s_lc

Una relaci n se puede armar con los tri ngulos del lado del objeto. En este caso la similitud nos permite escribir que el tama o del objeto a_o es a la distancia del objeto s_o al foco f es como el tama o de la imagen a_i es a la distancia del foco f:\\n\\n

$\displaystyle\frac{a_o}{s_o-f}=\displaystyle\frac{a_i}{f}$

Con la relaci n de similitud de los tri ngulos

$\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$

se puede mostrar que se cumple:

$\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$

(ID 3347)

$\displaystyle\frac{1}{ f_{vvd} }=( n -1)\left(\displaystyle\frac{1}{ R_1 }+\displaystyle\frac{1}{ R_2 }-\displaystyle\frac{( n -1)d}{ n R_1 R_2 }\right)$

1/ f_vvd =( n -1)*(1/ R_1 + 1/ R_2 -( n -1)* d /( n * R_1 * R_2 ))

(ID 3348)

$\displaystyle\frac{1}{ f_{ccd} }=-( n -1)\left(\displaystyle\frac{1}{ R_1 }+\displaystyle\frac{1}{ R_2 }+\displaystyle\frac{( n -1)d}{ n R_1 R_2 }\right)$

1/ f_ccd =-( n -1)*(1/ R_1 +1/ R_2 +( n -1)* d /( n * R_1 * R_2 ))

(ID 3349)

$\displaystyle\frac{1}{ f_{vcs} }=( n -1)\left(\displaystyle\frac{1}{ R_1 }-\displaystyle\frac{1}{ R_2 }+\displaystyle\frac{( n -1) d }{ n R_1 R_2 }\right)$

1/ f_vcs =( n -1)(1/ R_1 -1/ R_2 +( n -1)* d /(n * R_1 * R_2 ))

(ID 3350)

$\displaystyle\frac{1}{ f_{lv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_i }$

1/ f_lv =1/ s_o + 1/ s_i

(ID 3353)

$\displaystyle\frac{1}{ f_c }=\displaystyle\frac{1}{ D - s_i }+ \displaystyle\frac{1}{ s_b }$

1/ f_c =1/( D - s_i ) + 1/ s_b

(ID 3354)

$\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ D -\displaystyle\frac{1}{\displaystyle\frac{1}{ f_{lv} }-\displaystyle\frac{1}{ s_b }}}=\displaystyle\frac{1}{ f_c }$

1/ s_o + 1/( D -1/(1/ f_lv -1/ s_b ))=1/ f_c

Como es

$\displaystyle\frac{1}{ f_{lv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_i }$

\\n\\nse tiene que\\n\\n

$ s_i = \displaystyle\frac{1}{\displaystyle\frac{1}{ f_l } - \displaystyle\frac{1}{ s_o }}$

con lo que

$\displaystyle\frac{1}{ f_c }=\displaystyle\frac{1}{ D - s_i }+ \displaystyle\frac{1}{ s_b }$

se obtiene

$\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ D -\displaystyle\frac{1}{\displaystyle\frac{1}{ f_{lv} }-\displaystyle\frac{1}{ s_b }}}=\displaystyle\frac{1}{ f_c }$

(ID 3355)

$\displaystyle\frac{1}{ f_{cvs} }=\displaystyle\frac{( n -1)^2 d }{ n R ^2}$

1/ f_cvs =( n -1)^2* d /( n * R ^2)

(ID 3429)

$\displaystyle\frac{1}{ f_{vcs} }=\displaystyle\frac{( n -1)^2 d }{ n R ^2}$

1/ f_vcs =( n -1)^2* d /( n * R ^2)

(ID 3430)

$\displaystyle\frac{1}{ f_{csd} }=-( n -1)\left(\displaystyle\frac{2}{ R } +\displaystyle\frac{( n -1) d }{ n R ^2}\right)$

1/ f_csd =-( n -1)*(2/ R + ( n -1)* d /( n * R ^2))

(ID 3431)

$\displaystyle\frac{1}{ f_{vsd} }=( n -1)\left(\displaystyle\frac{2}{ R }-\displaystyle\frac{( n -1) d }{ n R ^2}\right)$

1/ f_vsd =( n -1)*(2/ R -( n -1)* d /( n * R ^2))

(ID 3432)

$D=\displaystyle\frac{1}{f}$

D =1/ f

(ID 3449)

Ejemplos

Definir la geometr a del lente optico

Finalmente podemos escoger el tipo de curvatura y si se asume que el anteojo tendr un grosor d podemos calcular el radio correspondiente.

Para simplificar el calculo consideraremos que la curvatura por ambos es igual. El tipo de curvatura se puede concluir simplemente por el tipo de patolog a.

(ID 533)

Geometr a del lente

Correcci n con Lentes

Lentes

(ID 1864)

Error de ojo y lente biconvexo

Hipermetrop a

(ID 1862)

Error de ojo y lente biconcavo

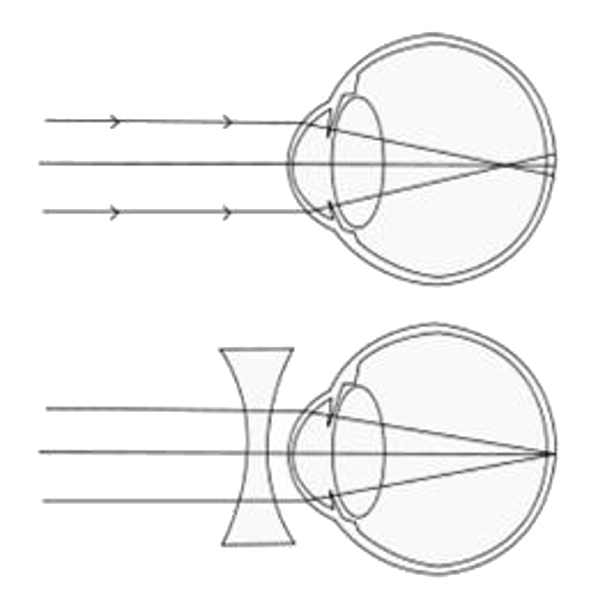
Miop a

(ID 1863)

Multiples lentes

Cuando se acoplan dos lentes con sus respectivos focos, el primer lente genera una imagen que funciona como objeto para el segundo lente que a su vez genera una imagen de una imagen:

(ID 9465)

Posici n y foco de lentes concavos

Por similitud de los tri ngulos de los tama os del objeto y la imagen y las posiciones del objeto y foco permite por similitud de tri ngulos mostrar que:

$\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$

(ID 3347)

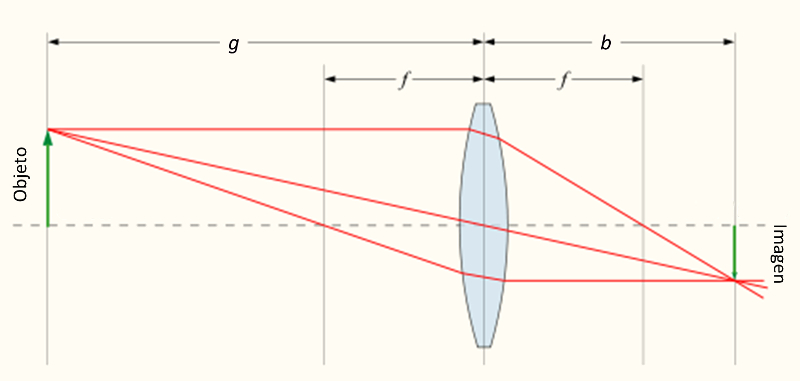
Proporciones de tama o y posici n de lentes concavos

Para cualquier lente se puede dibujar haces caracter sticos con los cuales se puede por similitud mostrar que los tama os del objeto y la imagen est n en la misma proporci n que sus distancias hasta el elemento ptico (lente o espejo).

Si el objeto tiene un tama o a_o, esta a una distancia s_o del lente, la imagen es de un tama o a_i y esta a una distancia s_i, por similitud de los tri ngulos se puede mostrar que

$\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$

(ID 3346)

Ecuaci n del foco del lente cristalino

Si observamos la secci n imagen (entre lente y cristalino) - cristalino - imagen sobre la retina, se puede aplicar la relaci n entre foco f, distancia a objeto s_o y distancia a imagen s_i:

$\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$

En este caso no disponemos de la distancia entre imagen entre lente y cristalino y cristalino. Sin embargo se se define la la distancia entre lente y cristalino como D y se emplea la distancia entre lente ptico e imagen s_i se puede calcular la distancia entre imagen y cristalino de D-s_i. Como en este caso el foco es f_e y la distancia entre cristalino y retina es s_e se tiene que:

$\displaystyle\frac{1}{ f_c }=\displaystyle\frac{1}{ D - s_i }+ \displaystyle\frac{1}{ s_b }$

donde f_e es el foco del cristalino, D-s_i la distancia de la imagen creada por el lente ptico y s_e la distancia donde el lente ptico proyecta la imagen. En este caso la distancia s_e es la distancia entre cristalino y retina.

(ID 3354)

Ecuaci n distancia lente optico cristalino

De la ecuaci n para el foco del lente ptico f_l

$\displaystyle\frac{1}{ f_{lv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_i }$

y la del cristalino f_e

$\displaystyle\frac{1}{ f_c }=\displaystyle\frac{1}{ D - s_i }+ \displaystyle\frac{1}{ s_b }$

la distancia entre lente y cristalino D y las distancias entre objeto y lente s_o y entre cristalino y retina s_e se puede eliminar la distancia de la imagen s_i y calcular directamente el foco del lente ptico que se necesita:

$\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ D -\displaystyle\frac{1}{\displaystyle\frac{1}{ f_{lv} }-\displaystyle\frac{1}{ s_b }}}=\displaystyle\frac{1}{ f_c }$

donde f_l es el foco del lente ptico, s_o la distancia al objeto al lente ptico y s_i la distancia donde el lente ptico proyecta la imagen.

(ID 3355)

Ecuaci n del foco para el lentes opticos

Si observamos la secci n objeto - lente ptico - imagen (entre lente y cristalino) se puede aplicar la relaci n entre foco f, distancia a objeto s_o y distancia a imagen s_i:

$\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$

Si en este caso el foco es f_l, la distancia al objeto es s_o y la distancia lente a imagen s_i se tiene que:

$\displaystyle\frac{1}{ f_{lv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_i }$

donde f_l es el foco del lente ptico, s_o la distancia al objeto al lente ptico y s_i la distancia donde el lente ptico proyecta la imagen.

(ID 3353)

Dioptria

Para caracterizar los problemas de visi n se indica la dioptr a. Si esta es negativa estamos frente a un caso de miop a (imagen se forma delante de la retina), si es positiva de hipermetropia (imagen se forma detr s de la retina).

La dioptr a D se calcula simplemente invirtiendo el valor del foco del lente ptico necesario y se expresa en el inverso del metro 1/m y se acorta con Dp.

Por ello tenemos que si f es el foco:

$D=\displaystyle\frac{1}{f}$

(ID 3449)

Situaci n Lente Concavo-Convexo

Lente Convexo-Concavo grueso

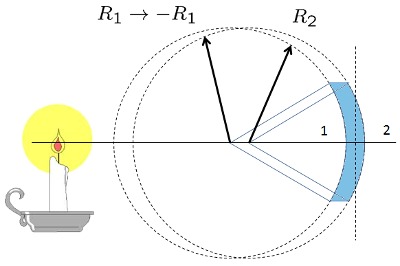
(ID 1860)

Situaci n Lente Convexo-C ncavo

Lente Concavo-Convexo grueso

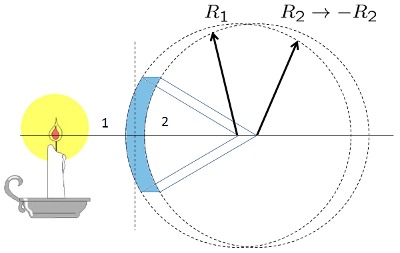
(ID 1859)

C lculo del f co de un lente bi-convexo grueso sim trico

Una caso especial es aquel en que los radios son iguales, o sea R=R_1=R_2. Por ello el foco se calcula de:

$\displaystyle\frac{1}{ f_{vsd} }=( n -1)\left(\displaystyle\frac{2}{ R }-\displaystyle\frac{( n -1) d }{ n R ^2}\right)$

(ID 3432)

C lculo del foco de un lente bi-convexo grueso

Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene un indice de refracci n n, un grosor en el centro de d y las curvaturas son R_1 y R_2, el foco f se calcula con

$\displaystyle\frac{1}{ f_{vvd} }=( n -1)\left(\displaystyle\frac{1}{ R_1 }+\displaystyle\frac{1}{ R_2 }-\displaystyle\frac{( n -1)d}{ n R_1 R_2 }\right)$

(ID 3348)

C lculo del foco de un lente convexo-concavo grueso sim trico

Una caso especial es aquel en que los radios son iguales, o sea R=R_1=R_2. Por ello el foco se calcula de:

$\displaystyle\frac{1}{ f_{vcs} }=\displaystyle\frac{( n -1)^2 d }{ n R ^2}$

(ID 3430)

C lculo del foco de un lente convexo-c ncavo grueso

Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene vidrio con indice de refracci n n, un grosor en el centro de d y las curvaturas son R_1 y R_2, se puede calcular el foco f. Para ello basta tomar la ecuaci n del lente bi-convexo e introducir el radios de curvatura R_2 con el signo negativo:

$\displaystyle\frac{1}{ f_{vcs} }=( n -1)\left(\displaystyle\frac{1}{ R_1 }-\displaystyle\frac{1}{ R_2 }+\displaystyle\frac{( n -1) d }{ n R_1 R_2 }\right)$

(ID 3350)

Dise o lente biconvexo

Lente Bi-Convexo grueso

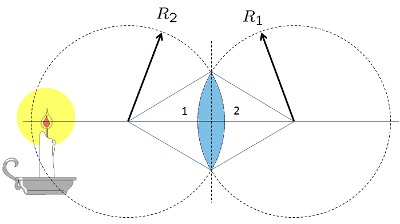
(ID 1857)

Situaci n Lente Biconcavo

Lente Bi-Concavo grueso

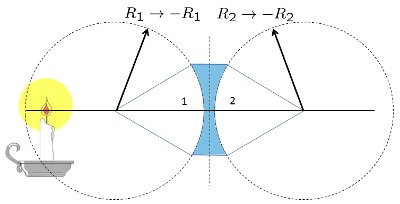
(ID 1858)

C lculo del f co de un lente bi-concavo grueso sim trico

Una caso especial es aquel en que los radios son iguales, o sea R=R_1=R_2. Por ello el foco se calcula de:

$\displaystyle\frac{1}{ f_{csd} }=-( n -1)\left(\displaystyle\frac{2}{ R } +\displaystyle\frac{( n -1) d }{ n R ^2}\right)$

(ID 3431)

C lculo del foco de un lente concavo-convexo grueso sim trico

Una caso especial es aquel en que los radios son iguales, o sea R=R_1=R_2. Por ello el foco se calcula de:

$\displaystyle\frac{1}{ f_{cvs} }=\displaystyle\frac{( n -1)^2 d }{ n R ^2}$

(ID 3429)

C lculo del foco de un lente bi-c ncavo grueso

$\displaystyle\frac{1}{ f_{ccd} }=-( n -1)\left(\displaystyle\frac{1}{ R_1 }+\displaystyle\frac{1}{ R_2 }+\displaystyle\frac{( n -1)d}{ n R_1 R_2 }\right)$

(ID 3349)

ID:(292, 0)