Benützer:
Multiples lentes
Übung 
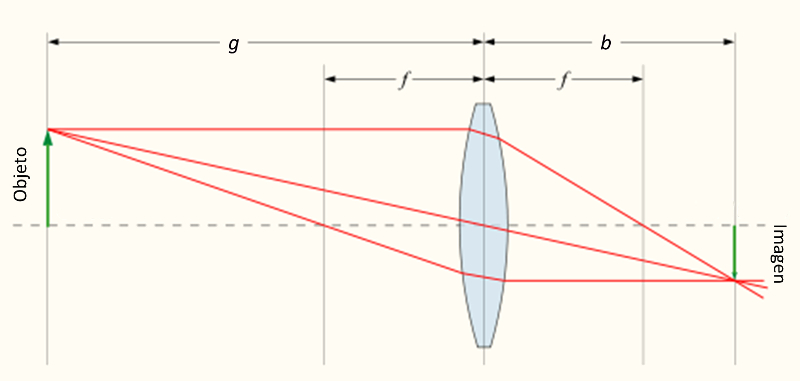
Cuando se acoplan dos lentes con sus respectivos focos, el primer lente genera una imagen que funciona como objeto para el segundo lente que a su vez genera una imagen de una imagen:
ID:(9465, 0)
Uso de Lentes
Beschreibung
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
Una relaci n se puede armar con los tri ngulos del lado del objeto. En este caso la similitud nos permite escribir que el tama o del objeto
$\displaystyle\frac{a_o}{s_o-f}=\displaystyle\frac{a_i}{f}$
Con la relaci n de similitud de los tri ngulos
| $\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$ |
se puede mostrar que se cumple:
| $\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$ |
(ID 3347)
Como es
| $\displaystyle\frac{1}{ f_{lv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_i }$ |
\\n\\nse tiene que\\n\\n
$ s_i = \displaystyle\frac{1}{\displaystyle\frac{1}{ f_l } - \displaystyle\frac{1}{ s_o }}$
con lo que
| $\displaystyle\frac{1}{ f_c }=\displaystyle\frac{1}{ D - s_i }+ \displaystyle\frac{1}{ s_b }$ |
se obtiene
| $\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ D -\displaystyle\frac{1}{\displaystyle\frac{1}{ f_{lv} }-\displaystyle\frac{1}{ s_b }}}=\displaystyle\frac{1}{ f_c }$ |
(ID 3355)
(ID 3449)
Beispiele
Correcci n con Lentes
(ID 1864)
(ID 1862)
(ID 1863)
Cuando se acoplan dos lentes con sus respectivos focos, el primer lente genera una imagen que funciona como objeto para el segundo lente que a su vez genera una imagen de una imagen:
(ID 9465)
Por similitud de los tri ngulos de los tama os del objeto y la imagen y las posiciones del objeto y foco permite por similitud de tri ngulos mostrar que:
| $\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$ |
(ID 3347)
F r jedes Objektiv k nnen Sie charakteristische Strahlen zeichnen, mit denen Sie auf hnliche Weise zeigen k nnen, dass die Gr en des Objekts und des Bildes im gleichen Verh ltnis stehen wie ihre Abst nde zum optischen Element (Objektiv oder Spiegel).
Wenn das Objekt eine Gr e
| $\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$ |
(ID 3346)
Si observamos la secci n imagen (entre lente y cristalino) - cristalino - imagen sobre la retina, se puede aplicar la relaci n entre foco
| $\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$ |
En este caso no disponemos de la distancia entre imagen entre lente y cristalino y cristalino. Sin embargo se se define la la distancia entre lente y cristalino como
| $\displaystyle\frac{1}{ f_c }=\displaystyle\frac{1}{ D - s_i }+ \displaystyle\frac{1}{ s_b }$ |
donde
(ID 3354)
De la ecuaci n para el foco del lente ptico
| $\displaystyle\frac{1}{ f_{lv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_i }$ |
y la del cristalino
| $\displaystyle\frac{1}{ f_c }=\displaystyle\frac{1}{ D - s_i }+ \displaystyle\frac{1}{ s_b }$ |
la distancia entre lente y cristalino
| $\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ D -\displaystyle\frac{1}{\displaystyle\frac{1}{ f_{lv} }-\displaystyle\frac{1}{ s_b }}}=\displaystyle\frac{1}{ f_c }$ |
donde
(ID 3355)
Si observamos la secci n objeto - lente ptico - imagen (entre lente y cristalino) se puede aplicar la relaci n entre foco
| $\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$ |
Si en este caso el foco es
| $\displaystyle\frac{1}{ f_{lv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_i }$ |
donde
(ID 3353)
$D=\displaystyle\frac{1}{f}$
(ID 3449)
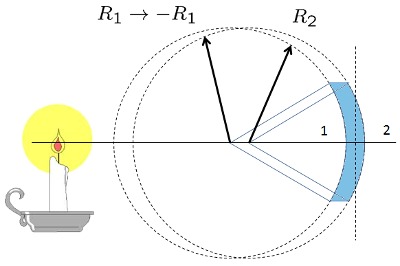
Lente Convexo-Concavo grueso
(ID 1860)
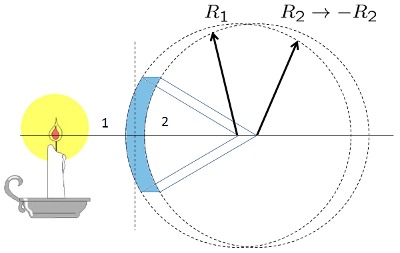
Lente Concavo-Convexo grueso
(ID 1859)
Una caso especial es aquel en que los radios son iguales, o sea
| $\displaystyle\frac{1}{ f_{vsd} }=( n -1)\left(\displaystyle\frac{2}{ R }-\displaystyle\frac{( n -1) d }{ n R ^2}\right)$ |
(ID 3432)
Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene un indice de refracci n
| $\displaystyle\frac{1}{ f_{vvd} }=( n -1)\left(\displaystyle\frac{1}{ R_1 }+\displaystyle\frac{1}{ R_2 }-\displaystyle\frac{( n -1)d}{ n R_1 R_2 }\right)$ |
(ID 3348)
Una caso especial es aquel en que los radios son iguales, o sea
| $\displaystyle\frac{1}{ f_{vcs} }=\displaystyle\frac{( n -1)^2 d }{ n R ^2}$ |
(ID 3430)
Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene vidrio con indice de refracci n
| $\displaystyle\frac{1}{ f_{vcs} }=( n -1)\left(\displaystyle\frac{1}{ R_1 }-\displaystyle\frac{1}{ R_2 }+\displaystyle\frac{( n -1) d }{ n R_1 R_2 }\right)$ |
(ID 3350)
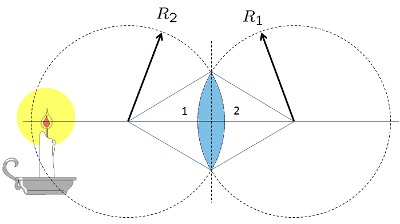
Lente Bi-Convexo grueso
(ID 1857)
Lente Bi-Concavo grueso
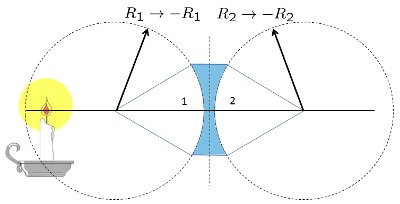
(ID 1858)
Una caso especial es aquel en que los radios son iguales, o sea
| $\displaystyle\frac{1}{ f_{csd} }=-( n -1)\left(\displaystyle\frac{2}{ R } +\displaystyle\frac{( n -1) d }{ n R ^2}\right)$ |
(ID 3431)
Una caso especial es aquel en que los radios son iguales, o sea
| $\displaystyle\frac{1}{ f_{cvs} }=\displaystyle\frac{( n -1)^2 d }{ n R ^2}$ |
(ID 3429)
Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene vidrio con indice de refracci n
| $\displaystyle\frac{1}{ f_{ccd} }=-( n -1)\left(\displaystyle\frac{1}{ R_1 }+\displaystyle\frac{1}{ R_2 }+\displaystyle\frac{( n -1)d}{ n R_1 R_2 }\right)$ |
(ID 3349)
ID:(292, 0)