Benützer:
Auftrieb
Storyboard 
Wenn ein Körper in einem flüssigen Medium eingetaucht ist, erfährt er den Druck dieses Mediums. Da der Druck mit der Tiefe zunimmt, ist er am unteren Teil des Körpers größer als am oberen Teil, was eine Kraft nach oben zur Oberfläche erzeugt, die als Auftriebskraft bezeichnet wird. Wenn diese Kraft größer ist als die Schwerkraft des Körpers, wird er an die Oberfläche steigen und schwimmen. Ist sie geringer, wird sie die Geschwindigkeit des Sinkens verringern, aber der Körper wird weiter sinken, bis er den Boden berührt.
ID:(1609, 0)
Mechanismen
Iframe
Mechanismen
ID:(15480, 0)
Auftrieb
Konzept
Wenn ein Objekt, das an einem Dynamometer hängt, in eine Flüssigkeit eingetaucht wird, wird beobachtet, dass die vom Dynamometer angezeigte Kraft abnimmt, was auf das Vorhandensein einer Auftriebskraft eine Auftriebskraft ($F_b$)8661,1 hinweist, die von der Flüssigkeit erzeugt wird.
Wenn ein Objekt schwimmt, muss die Auftriebskraft die Auftriebskraft ($F_b$)8661 gleich der die Schwerkraft ($F_g$)4977, was erklärt, dass es weder sinkt noch auftaucht.
ID:(11951, 0)
Druck um einen untergetauchten Körper
Konzept
Um den Auftrieb zu erklären, den ein untergetauchter Körper erfährt, ist es notwendig, die vertikalen Drücke zu untersuchen, denen er ausgesetzt ist. Da die Unterseite des Körpers tiefer liegt als die Oberseite, ist der Druck unten größer als oben, was zu einer Nettoaufwärtskraft führt, die den beobachteten Auftrieb erzeugt. Dieses Phänomen ist ähnlich, wenn ein Körper an der Oberfläche schwimmt, wo kein Wasserdruck auf ihn ausgeübt wird; Auch hier ist es der Druck am Boden, der den Auftrieb erzeugt.
Für den Fall, dass der Körper untergetaucht ist, erhalten wir daher:
$\Delta p = p_2 - p_1 = \rho_w g h_2-\rho_w g h_1=\rho_w g (h_2 - h_1) = \rho_w g d$
Oder ähnlich an der Oberfläche:
| $ \Delta p = \rho_w g d $ |
Schließlich wird die Auftriebskraft mithilfe der Druckdefinition ermittelt, die für die Druck an der Basis ($\Delta p$)10284 mit die Auftriebskraft ($F_b$)8661 und die Schwebender Körperabschnitt ($S_s$)10283 entspricht:
| $ \Delta p \equiv\displaystyle\frac{ F_b }{ S_s }$ |
ID:(11952, 0)
Archimedes Prinzip
Konzept
Ein Körper schwimmt, wenn die Auftriebskraft die Auftriebskraft ($F_b$)8661 gleich dem Gewicht des Körpers die Schwerkraft ($F_g$)4977 ist:
| $ F_b = F_g $ |
Dies impliziert, dass die Beziehung zwischen die Masse eines schwimmenden Objekts ($M_s$)8664 und die Masse der verdrängte Flüssigkeit ($M_b$)8663 festlegt:
| $ M_b = M_s $ |
Was dem Archimedes-Prinzip [1] entspricht.
das besagt:
Jeder schwimmende Körper verdrängt in der Flüssigkeit sein eigenes Gewicht.
[1] Peri ton Eightumenon (Von schwimmenden Körpern), Archimedes, 287 bis 212 v. Chr.
ID:(11956, 0)
Luftvolumen unter dem Schwimmerstand
Konzept
Angesichts von die Masse eines schwimmenden Objekts ($M_s$)8664 und die Masse der verdrängte Flüssigkeit ($M_b$)8663,
| $ M_b = M_s $ |
verhält sich zu die Objektdichte ($\rho_s$)8665 und der Objektvolumen ($V_s$)8666 wie
während es mit die Flüssigkeitsdichte ($\rho_w$)5407 und der Ballastvolumen ($V_w$)8668 zutrifft, dass
| $ M_b = \rho_w ( V_s + V_w )$ |
erhalten wir die Beziehung
| $ \rho_s V_s = \rho_w ( V_s + V_w )$ |
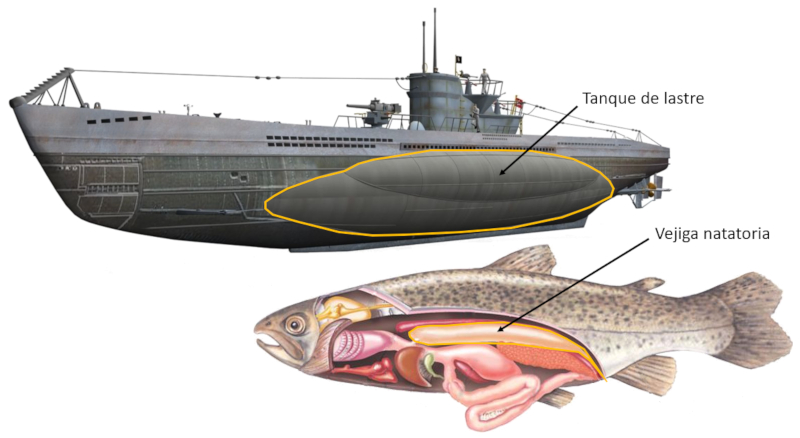
Daher kann ein Objekt mit einer höheren Dichte als Wasser schwimmen, solange es ein geringes Luftvolumen unterhalb der Wasserlinie (Oberfläche des Wassers) aufweist. Im Fall eines Bootes ist dies der Platz, der von der Ladung und/oder den Passagieren eingenommen wird, während es bei einem U-Boot die Ballasttanks und bei einem Fisch die Schwimmblase ist.
Es ist wichtig zu beachten, dass:
Für ein untergetauchtes Objekt hängen die Aufhängung, der Aufstieg oder der Abstieg nicht von der Tiefe ab, in der es sich befindet. Die Fähigkeit, Luft in den Ballasttank oder die Schwimmblase zu pumpen, hängt jedoch vom umgebenden Druck ab.
Die Dichte des Wassers ist im Meer nicht homogen, was bedeutet, dass ein untergetauchtes Objekt das verwendete Luftvolumen im Ballasttank oder der Schwimmblase anpassen muss, wenn es sich bewegt.
ID:(15706, 0)
Floatationsmethoden
Konzept
U-Boote und Fische haben die Fähigkeit, die Tiefe anzupassen, in der sie sich im Wasser aufhalten. Sie können an die Oberfläche aufsteigen (schwimmen) oder abtauchen, nur durch den Druck begrenzt, den sie aushalten können. Dies erreichen sie durch die Verwendung von Ballasttanks (bei U-Booten) und Schwimmblasen (bei Fischen), die Räume sind, in denen Luft sich ausdehnen kann und somit ein größeres Volumen des verdrängten Wassers einnimmt.
Um dies zu erreichen, kann die Gleichheit zwischen die Masse der verdrängte Flüssigkeit ($M_b$)8663 und die Masse eines schwimmenden Objekts ($M_s$)8664 in Bezug auf die Flüssigkeitsdichte ($\rho_w$)5407, die Objektdichte ($\rho_s$)8665 und der Objektvolumen ($V_s$)8666 umgeschrieben werden, was die Anpassung von der Ballastvolumen ($V_w$)8668 ermöglicht:
| $ \rho_s V_s = \rho_w ( V_s + V_w )$ |
wobei eine gleich oder die andere übertreffen kann. Zusammengefasst, wenn der Ballastvolumen ($V_w$)8668 erhöht wird, steigt die Auftriebskraft und das Objekt steigt auf; eine Reduzierung des Volumens führt zum Absinken. Wenn das Volumen gleich bleibt, bleiben sie in Schwebe.
An interesting study on how whales use the spermaceti organ to control buoyancy through heat and fats can be found in the study "Buoyancy Control as a Function of the Spermaceti Organ in the Sperm Whale" by Malcolm R. Clarke, published in J.mar.bio.Ass U.K. (1978) 58, 27-71.
ID:(11958, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ \Delta p = \rho_w g d $
Dp = rho_w * g * d
$ F_b = F_g $
F_b = F_g
$ F_b = \rho_w V_b g $
F_b = rho_w * V_b * g
$ F_g = M_s g $
F_g = m_g * g
$ M_b = M_s $
M_b = M_s
$ M_b = \rho_w ( V_s + V_w )$
M_b = rho_w *( V_s + V_w )
$ \Delta p \equiv\displaystyle\frac{ F_b }{ S_s }$
p = F / S
$ \rho_w \equiv\displaystyle\frac{ M_b }{ V_b }$
rho = M / V
$ \rho_s \equiv\displaystyle\frac{ M_s }{ V_s }$
rho = M / V
$ \rho_s V_s = \rho_w ( V_s + V_w )$
rho_s * V_s = rho_w *( V_s + V_w )
$ V_b = S_s d $
V = S * h
$ V_b = V_s + V_w $
V_b = V_s + V_w
ID:(15482, 0)
Volumen
Gleichung
Der Volumen ($V$)5226 von eine Abschnitt ($S$)5205,1, die sich entlang von der Höhe ($h$)5341 nicht ändert, ist gleich
| $ V_b = S_s d $ |
| $ V = S h $ |
Der Ausdruck bleibt gültig, auch wenn sich die Form, aber nicht der Wert, des Abschnitts die Abschnitt ($S$)5205 entlang der Höhe ändert, solange seine Gesamtfläche konstant bleibt.
ID:(3792, 0)
Definition des Drucks
Gleichung
Die Druck der Wassersäule ($p$)10114 wird aus die Kraft der Säule ($F$)10113 und die Column Abschnitt ($S$)6002 wie folgt berechnet:
| $ \Delta p \equiv\displaystyle\frac{ F_b }{ S_s }$ |
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
ID:(4342, 0)
Druck an der Basis
Gleichung
Die die Druck an der Basis ($\Delta p$)10284, die im tiefsten Plan des Körpers existiert, ist mit der Tiefgang des Objekts ($d$)8675, die Flüssigkeitsdichte ($\rho_w$)5407 und die Gravitationsbeschleunigung ($g$)5310 dann:
| $ \Delta p = \rho_w g d $ |
ID:(15484, 0)
Auftriebs Kraft, abhängig vom Volumen
Gleichung
Die Auftriebskraft ($F_b$)8661 kann in Bezug auf der Verdrängtes Volumen ($V_b$)8662, die Flüssigkeitsdichte ($\rho_w$)5407 und die Gravitationsbeschleunigung ($g$)5310 ausgedrückt werden mit:
| $ F_b = \rho_w V_b g $ |
Druck wird definiert als:
| $ \Delta p \equiv\displaystyle\frac{ F_b }{ S_s }$ |
Der Druckunterschied ist:
| $ \Delta p = \rho_w g \Delta h $ |
Die Querschnittsfläche des Körpers multipliziert mit seiner Höhe entspricht seinem Volumen:
| $ V_b = S_s d $ |
Daher ergibt sich die Auftriebskraft auf einen eingetauchten Körper als:
$F_b = S \Delta p = \rho S \Delta h g = \rho V_s g$
Das heißt:
| $ F_b = \rho_w V_b g $ |
Hinweis: Das hier betrachtete Volumen ist das untergetauchte Volumen. Wenn der Körper nicht vollständig eingetaucht ist, sollte nur das Volumen berücksichtigt werden, das die verdrängte Flüssigkeit entspricht.
ID:(11953, 0)
Schwerkraft
Gleichung
Die Schwerkraft ($F_g$)4977 basiert auf die Gravitationsmasse ($m_g$)8762 des Objekts und auf einer Konstanten, die die Intensität der Gravitation an der Oberfläche des Planeten widerspiegelt. Letztere wird durch die Gravitationsbeschleunigung ($g$)5310 identifiziert, was $9.8 m/s^2$ entspricht.
Daraus folgt, dass:
| $ F_g = M_s g $ |
| $ F_g = m_g g $ |
ID:(3241, 0)
Auftriebs
Gleichung
Wenn die Schwerkraft ($F_g$)4977 gleich die Auftriebskraft ($F_b$)8661 ist:
| $ F_b = F_g $ |
Die Auftriebskraft ($F_b$)8661 wird durch die Flüssigkeitsdichte ($\rho_w$)5407, der Verdrängtes Volumen ($V_b$)8662 und die Gravitationsbeschleunigung ($g$)5310 bestimmt als:
| $ F_b = \rho_w V_b g $ |
was die Schwerkraft ($F_g$)4977 mit die Masse eines schwimmenden Objekts ($M_s$)8664 entgegenwirkt:
| $ F_g = M_s g $ |
Wenn beide Kräfte gleich sind:
| $ F_b = F_g $ |
wird der Gegenstand schwimmen.
wird der Gegenstand schwimmen.
ID:(13406, 0)
Auftriebs, abhängig von der Masse
Gleichung
Wenn die Auftriebskraft ($F_b$)8661 und die Schwerkraft ($F_g$)4977 gleich sind, wird der Gegenstand schwimmen. In diesem Fall bedeutet das, dass die Masse eines schwimmenden Objekts ($M_s$)8664 gleich die Masse der verdrängte Flüssigkeit ($M_b$)8663 sein muss, was zu folgendem Ergebnis führt:
| $ M_b = M_s $ |
Die Auftriebskraft ($F_b$)8661 wird durch die Flüssigkeitsdichte ($\rho_w$)5407, der Verdrängtes Volumen ($V_b$)8662 und die Gravitationsbeschleunigung ($g$)5310 bestimmt als:
| $ F_b = \rho_w V_b g $ |
was die Schwerkraft ($F_g$)4977 mit die Masse eines schwimmenden Objekts ($M_s$)8664 entgegenwirkt gemäß:
| $ F_g = M_s g $ |
daher, mit die Masse der verdrängte Flüssigkeit ($M_b$)8663 und die Masse eines schwimmenden Objekts ($M_s$)8664,
$F_b = \rho_w V_w g = M_w g = M_s g = F_g$
ergibt sich:
| $ M_b = M_s $ |
Hinweis: Diese Beziehung ist nur möglich, wenn der Gegenstand 'weniger als Wasser wiegt', was bedeutet, dass das verdrängte Wasser ein gleiches oder größeres Volumen als der Gegenstand einnimmt.
ID:(11955, 0)
Masse und Dichte (1)
Gleichung
Die Dichte ($\rho$)10182 wird als das Verhältnis zwischen die Masse ($M$)5183 und der Volumen ($V$)5226 definiert, ausgedrückt als:
| $ \rho_w \equiv\displaystyle\frac{ M_b }{ V_b }$ |
| $ \rho \equiv\displaystyle\frac{ M }{ V }$ |
Diese Eigenschaft ist spezifisch für das betreffende Material.
ID:(3704, 1)
Masse und Dichte (2)
Gleichung
Die Dichte ($\rho$)10182 wird als das Verhältnis zwischen die Masse ($M$)5183 und der Volumen ($V$)5226 definiert, ausgedrückt als:
| $ \rho_s \equiv\displaystyle\frac{ M_s }{ V_s }$ |
| $ \rho \equiv\displaystyle\frac{ M }{ V }$ |
Diese Eigenschaft ist spezifisch für das betreffende Material.
ID:(3704, 2)
Volumen mit Ballastluft
Gleichung
Wenn ein Körper eingetaucht ist, wird der Ballastvolumen ($V_w$)8668 im Ballasttank mit der Objektvolumen ($V_s$)8666 im Gesamtvolumen von der Verdrängtes Volumen ($V_b$)8662 mit einbezogen. Daher haben wir:
| $ V_b = V_s + V_w $ |
ID:(12015, 0)
Verdrängte Wassermasse
Gleichung
Mit dem Volumen des verdrängten Wassers, das gleich der Summe von der Ballastvolumen ($V_w$)8668 und der Untergetauchtes Volumen ($V_s$)8667 ist, kann mit die Flüssigkeitsdichte ($\rho_w$)5407 Die Masse der verdrängte Flüssigkeit ($M_b$)8663 berechnet werden:
| $ M_b = \rho_w ( V_s + V_w )$ |
Da der Verdrängtes Volumen ($V_b$)8662 Der Untergetauchtes Volumen ($V_s$)8667 ist, aber einschließlich der Ballastvolumen ($V_w$)8668, haben wir
| $ V_b = V_s + V_w $ |
und die Gleichung für die Flüssigkeitsdichte ($\rho_w$)5407 dargestellt durch
| $ \rho_w \equiv\displaystyle\frac{ M_b }{ V_b }$ |
können wir die Masse der verdrängte Flüssigkeit ($M_b$)8663 berechnen als
| $ M_b = \rho_w ( V_s + V_w )$ |
ID:(12016, 0)
Luftvolumen unter dem Schwimmerstand
Gleichung
Die Float-Bedingung ist mit der Ballastvolumen ($V_w$)8668, die Flüssigkeitsdichte ($\rho_w$)5407, die Objektdichte ($\rho_s$)8665 und der Objektvolumen ($V_s$)8666:
| $ \rho_s V_s = \rho_w ( V_s + V_w )$ |
Angesichts von die Masse eines schwimmenden Objekts ($M_s$)8664 und die Masse der verdrängte Flüssigkeit ($M_b$)8663,
| $ M_b = M_s $ |
verhält sich zu die Objektdichte ($\rho_s$)8665 und der Objektvolumen ($V_s$)8666 wie
während es mit die Flüssigkeitsdichte ($\rho_w$)5407 und der Ballastvolumen ($V_w$)8668 zutrifft, dass
| $ M_b = \rho_w ( V_s + V_w )$ |
erhalten wir die Beziehung
| $ \rho_s V_s = \rho_w ( V_s + V_w )$ |
ID:(11978, 0)