Benützer:
Auftrieb Stabilität
Storyboard 
Die durch den Auftrieb entstehende Kraft wirkt im Zentrum des verdrängten Volumens, das in der Regel unterhalb des Massenschwerpunkts des Objekts im Wasser liegt. Dieses Kräftepaar erzeugt Drehmomente, die das Objekt stabilisieren oder destabilisieren können. Im letzteren Fall könnte es sogar umkippen. Dieses Prinzip gilt sowohl für unbewegliche Objekte als auch für lebende Organismen, die aufgrund von Krankheiten Schwierigkeiten haben können, eine aufrechte Position zu halten.
ID:(1610, 0)
Mechanismen
Iframe
Mechanismen
ID:(15481, 0)
Die Vasa-Katastrophe
Beschreibung
Die schwedische Kriegsschiff Vasa ist ein bekanntes Beispiel für ein instabiles Schiff. Am 10. August 1628, nur 20 Minuten nach dem Verlassen der Werft auf seiner Jungfernfahrt im Hafen von Stockholm, kenterte und sank das Schiff:
Das Design des Schiffes war fehlerhaft, da die schmale Konstruktion für hohe Geschwindigkeiten und die hohe Struktur für 64 Kanonen, eine erhebliche Anzahl, gedacht war. Dieses Design machte das Schiff jedoch von Natur aus instabil, was zu seiner Kenterung bei der ersten Windböe führte.
Glücklicherweise sank das Schiff in flachem Wasser und wurde für 333 Jahre in Salzwasser konserviert, bis es 1961 geborgen wurde. Zunächst wurde das Schiff nass gehalten und dann langsam das Wasser durch eine Wachsmischung ersetzt, so dass es heute trocken im Museum ausgestellt werden kann, nur wenige Meter von der Stelle entfernt, wo es sank.
Die Vasa dient als Mahnung in der Schiffbauindustrie und zeigt die Bedeutung von sorgfältigem Design und Stabilität auf. Ihre Ausstellung im Museum ist eine beliebte Attraktion und zieht Besucher aus aller Welt an, um dieses bemerkenswerte Stück Seefahrtgeschichte zu sehen.
ID:(11977, 0)
Angriffspunkt des Auftriebs
Beschreibung
Der Angriffspunkt der Auftriebskraft entspricht dem Schwerpunkt des verdrängten Flüssigkeitsvolumens:
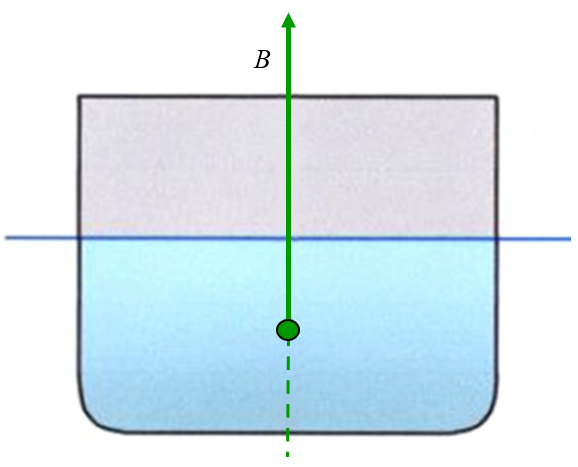
Bei einem typischen Boot mit quadratischem Profil entspricht dies einem Punkt in der Mitte des Tiefgangs (Eintauchtiefe).
ID:(11957, 0)
Metacenter definieren
Beschreibung
Wenn eine seitliche Kraft auf das Objekt ausgeübt wird und es gekippt wird, kann beobachtet werden, dass sich der Punkt, an dem die Auftriebskraft wirkt, von der Achse entfernt. Zeichnet man eine vertikale Linie von dieser neuen Position aus, so wird die Linie an einem Punkt mit der Achse gekreuzt, der als Metazentrum bezeichnet wird:
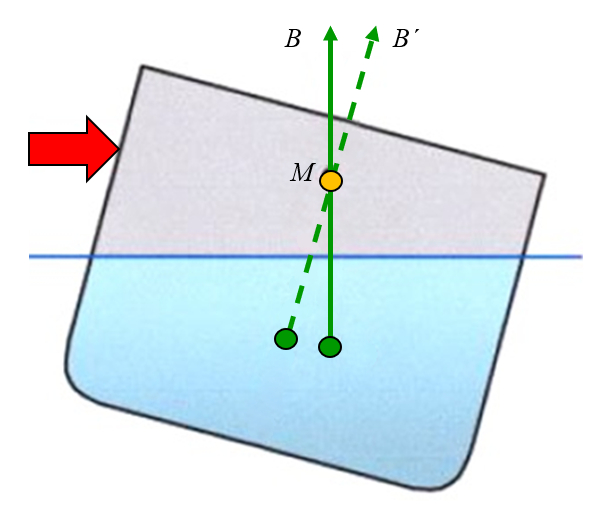
ID:(11959, 0)
Schwerkraftwirkung
Konzept
Die Schwerkraft wirkt auf den Schwerpunkt, der normalerweise über dem Angriffspunkt der Auftriebskraft liegt, aber über oder unter dem Metazentrum liegen kann:
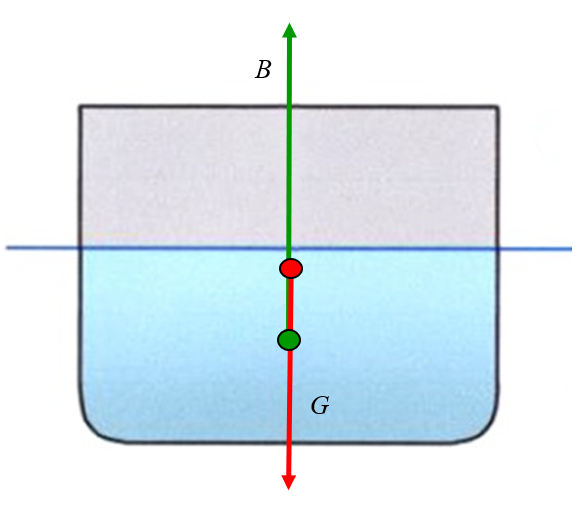
ID:(11960, 0)
Stabile Situation
Beschreibung
Wenn der Metazentrum über dem Schwerpunkt liegt, erzeugt die Schwerkraft ein Drehmoment, das dazu neigt, das Objekt zu stabilisieren. Es ist so, als ob das Objekt vom Metazentrum aufgehängt wäre und die Schwerkraft Rotationen um dieses erzeugt. Wenn der Schwerpunkt unter dem Metazentrum liegt, erzeugt das Drehmoment eine Drehung zum Achsenpunkt hin, d.h. es neigt dazu, die Schräglage zu korrigieren und das Objekt zu stabilisieren:
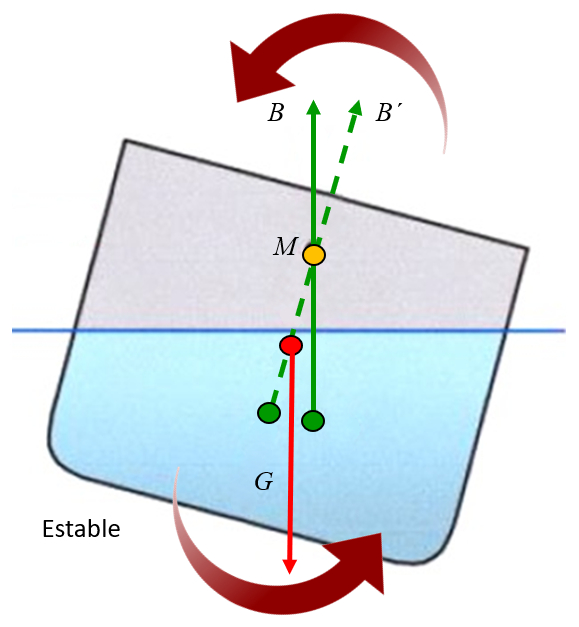
ID:(11961, 0)
Metazentrum unterhalb des Schwerpunkts
Beschreibung
Wenn der Metazentrum über oder unter dem Schwerpunkt liegt, kann dies leicht passieren, wenn man eine Last oben auf dem Körper hinzufügt, was dazu führt, dass der Schwerpunkt steigt und das System instabil wird.
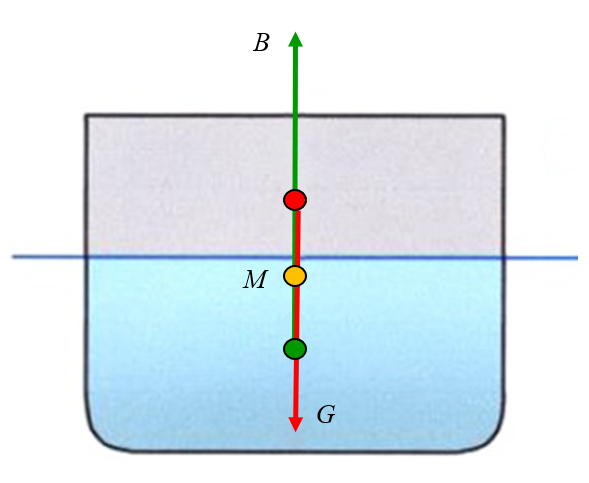
Hinweis: Um die Stabilität zu erhalten, ist es wichtig, die Last in einer niedrigen Position (am Boden des Bootes) zu positionieren.
ID:(11962, 0)
Instabile Situation
Beschreibung
Wenn der Metazentrum unter dem Schwerpunkt liegt, erzeugt die Schwerkraft ein Drehmoment, das dazu neigt, das Objekt zu destabilisieren. Es ist so, als ob das Objekt vom Metazentrum aufgehängt wäre und die Schwerkraft Rotationen um dieses erzeugt. Wenn der Schwerpunkt über dem Metazentrum liegt, erzeugt das Drehmoment eine Drehung, die es vom Achsenpunkt entfernt, d.h. es neigt dazu, die Neigung zu erhöhen und das Objekt zu destabilisieren:
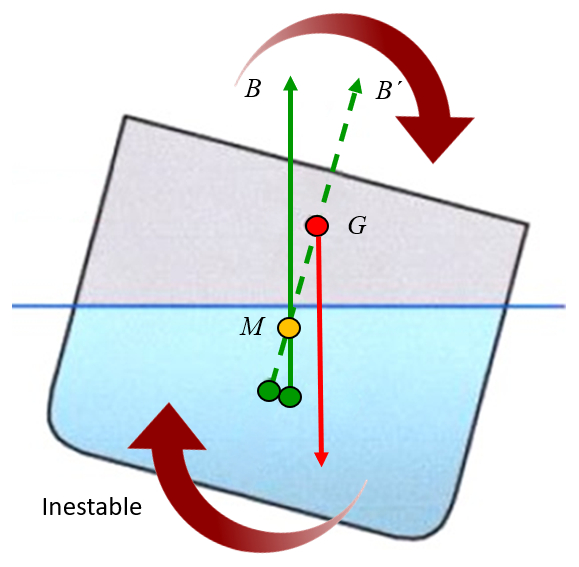
ID:(11963, 0)
Modell eines Schiffsrumpfes
Beschreibung
Das Modell des Schiffsrumpfes wird auf ein Parallelepipid mit den Längen von der Mittlere Länge des Parallelepipeds ($a$)8673, der Halbe Breite des Parallelepipeds ($b$)8674 und die Halbe Höhe des Parallelepipeds ($c$)8672 reduziert, was zu Abmessungen von $2a \times 2b \times 2c$ führt, mit einem Tiefgang von ein Tiefgang des Objekts ($d$)8675,1:
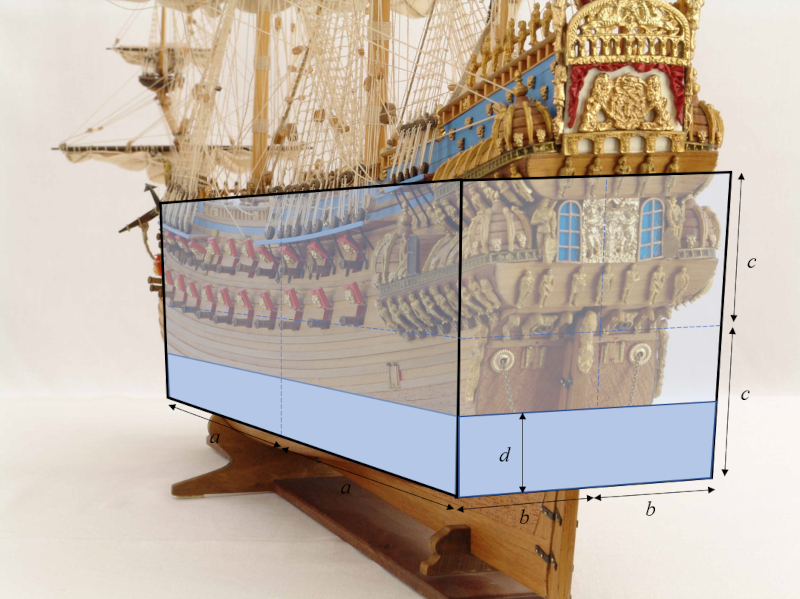
ID:(11969, 0)
Vereinfachtes Modell: gerades Parallelepiped
Konzept
Ein Modell, das für Boote verwendet wird, ist das eines geraden Parallelepipeds mit Längen von der Mittlere Länge des Parallelepipeds ($a$)8673, der Halbe Breite des Parallelepipeds ($b$)8674 und die Halbe Höhe des Parallelepipeds ($c$)8672, und einem Massenschwerpunkt in seinem geometrischen Zentrum. Wenn es ins Wasser gelegt wird, sinkt der Körper auf eine Tiefe von ein Tiefgang des Objekts ($d$)8675,1. Die Position des Zentrums, an dem die Auftriebskraft wirkt, ist in folgendem Bild zu sehen, mit den Koordinaten die Auftrieb Angriffspunkt ($z_B$)8669, die Höhe des Schwerpunkts ($z_G$)8670 und die Höhe des Metazentrums ($z_M$)8671:
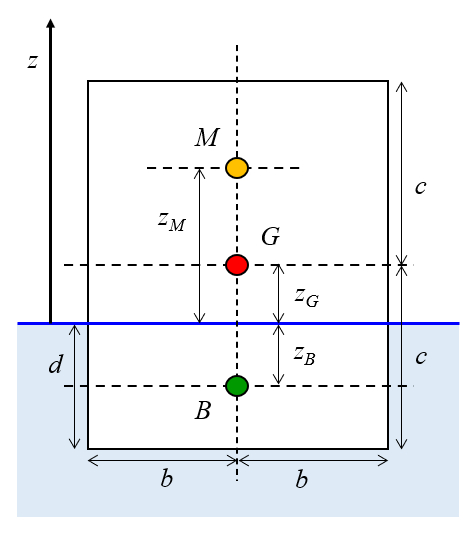
Daher ist die Höhe des Schwerpunkts ($z_G$)8670 gleich
| $ z_G = c - d $ |
ID:(11964, 0)
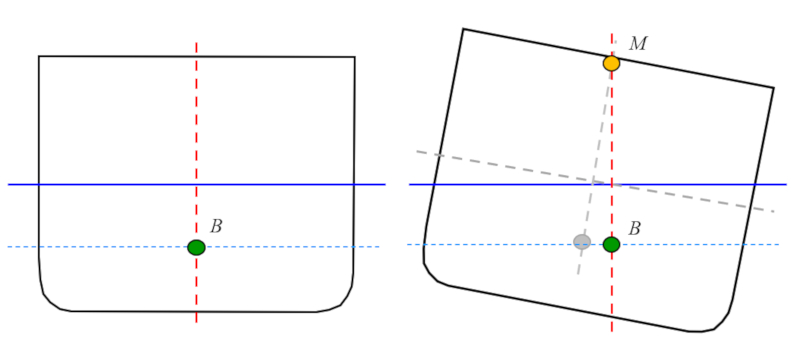
Definition der Position des Metazentrums
Beschreibung
Das Metazentrum wird berechnet, indem der Schwerpunkt des gekippten Körpers unter der Bedingung bestimmt wird, dass die Fläche unter der Wasserlinie (blaue Linie) konstant bleibt:
ID:(11979, 0)
Berechnung der Lage des Massenschwerpunktes des verdrängten Wassers
Beschreibung
Wenn das Boot krängt, bewegt sich auf der einen Seite ein größerer Wasserabschnitt und auf der gegenüberliegenden Seite derselbe kleinere Wasserabschnitt. Der Massenschwerpunkt verschiebt sich also von der Mitte in den Sektor mit der größten Verschiebung, die durch berechnet wird
$\bar{x} = \displaystyle\frac{\displaystyle\sum_i m_i x_i}{\displaystyle\sum_i m_i}$
Die Masse ist proportional zum Querschnitt, der aus der Halbe Breite des Parallelepipeds ($b$)8674 und der Tiefgang des Objekts ($d$)8675 berechnet wird durch:
$2b d$
Alle Massen, die auf beiden Seiten der Achse versetzt sind, tragen nicht zum Zähler bei und nur die beiden angegebenen Dreiecke ergeben eine Fläche mit der Krängungswinkel ($\phi$)10285
$b^2\phi$
Gewichten Sie die Position des Massenschwerpunkts der Dreiecke
$\displaystyle\frac{2b}{3}$
Was ist in der Grafik zu sehen:
Daher beträgt der Abstand vom Massenschwerpunkt des von der Achse verschobenen Wassers
$\displaystyle\frac{\displaystyle\frac{2b}{3} b^2\phi}{2bd}=\displaystyle\frac{b^2\phi}{3d}$
ID:(14248, 0)
Berechnung der Position des Metazentrums
Beschreibung
Wenn ein Schiff bei der Krängungswinkel ($\phi$)10285 krängt, verschiebt sich der Schwerpunkt des verdrängten Wassers um der Halbe Breite des Parallelepipeds ($b$)8674 und der Mittlere Länge des Parallelepipeds ($a$)8673 um eine Distanz von:
$\displaystyle\frac{b^2\phi}{3d}$
Da dieser Abstand der Bogen des Kreises ist, der um das Metazentrum gezogen werden kann, beträgt der Abstand zwischen dem Metazentrum und dem Massenschwerpunkt des verdrängten Wassers, der dem Radius entspricht:
$\displaystyle\frac{b^2}{3d}$
Daher muss bei der Position des Metazentrums berücksichtigt werden, dass sich das Koordinatenzentrum auf der Höhe der Wasseroberfläche befindet, also einen Abstand $d/2$ über dem Massenschwerpunkt des verdrängten Wassers:
mit die Höhe des Metazentrums ($z_M$)8671:
| $ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$ |
ID:(11967, 0)
Analyse der Stabilitätsbedingung für das Parallelepiped
Beschreibung
Um sicherzustellen, dass der Quader stabil ist, muss die Höhe des Metazentrums ($z_M$)8671 immer größer oder gleich die Höhe des Schwerpunkts ($z_G$)8670 sein, das heißt
| $ z_M \geq z_G $ |
Daher ist mit die Höhe des Schwerpunkts ($z_G$)8670 als dem Angriffspunkt der gegebenen Auftriebskraft mit die Halbe Höhe des Parallelepipeds ($c$)8672 und der Tiefgang des Objekts ($d$)8675:
| $ z_G = c - d $ |
und die Höhe des Metazentrums ($z_M$)8671 mit der Halbe Breite des Parallelepipeds ($b$)8674:
| $ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$ |
erhalten wir die Stabilitätszustand eines Schwimmkörpers ($e$)9835:
| $ e = \displaystyle\frac{1}{6}\displaystyle\frac{ b ^2}{ c ^2} - \displaystyle\frac{ d }{2 c }\left(1-\displaystyle\frac{ d }{2 c }\right)$ |
Das bedeutet, dass es im Diagramm $b/c$ (Breite/Tiefe) versus $d/2c$ (Tiefe/Höhe) einen Bereich gibt, in dem das System stabil und in seinem Komplement instabil ist:
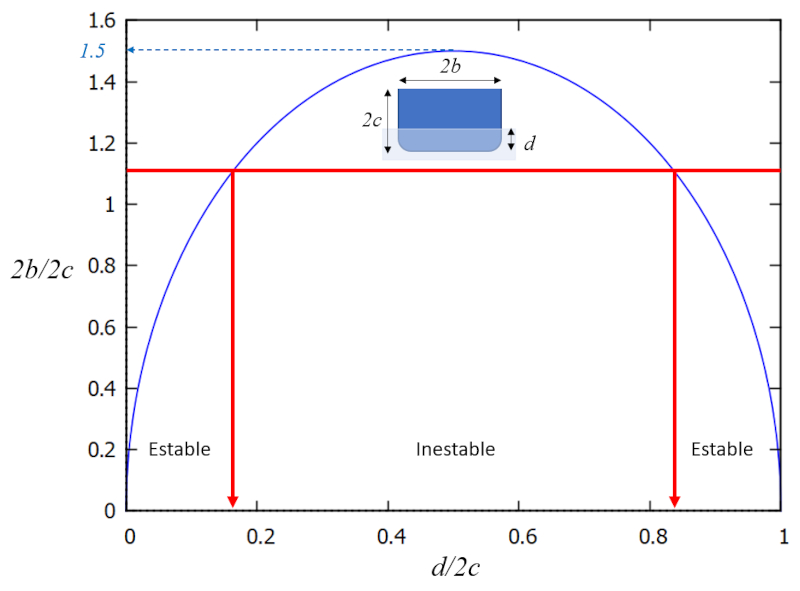
Mit anderen Worten: Stabilität wird mit großen Werten von $b/c$ (Breite größer als Tiefgang) erreicht. Im Fall des Vasa-Schiffes bestand das Problem darin, dass das Schiff für seine Breite zu hoch war. Eine Lösung wäre gewesen, es tiefer zu versenken oder einen höheren $d/c$-Wert zu erreichen, um die Zone der Instabilität zu vermeiden. Dies war jedoch aufgrund der Öffnungen für die Kanonen, durch die Wasser eingedrungen wäre, nicht möglich.
Weitere Informationen zu Buildfehlern finden Sie unter Why The Vasa Sank: 10 Problems and Some Antidotes for Software Projects, Richard E. Fairley, Mary Jane Willshire, März/April 2003 IEEE SOFTWARE, das für Softwareprojekte gilt.
ID:(11976, 0)
Analyse des Wasa-Falls
Beschreibung
Durch die Untersuchung der Baupläne der Vasa kann man die Koeffizienten des Verhältnisses zwischen Breite und Höhe sowie zwischen Tiefgang und Höhe abschätzen. Diese Analyse zeigt, dass das Schiff instabil ist:
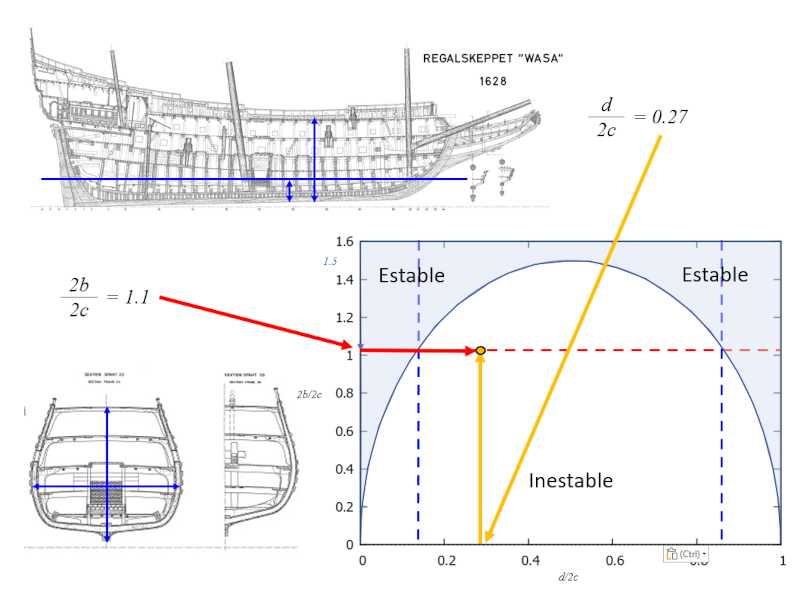
ID:(14247, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ e = \displaystyle\frac{1}{6}\displaystyle\frac{ b ^2}{ c ^2} - \displaystyle\frac{ d }{2 c }\left(1-\displaystyle\frac{ d }{2 c }\right)$
e = b ^2/(6* c ^2) - d *(1 - d /(2* c ))/(2* c )
$ M_b = M_s $
M_b = M_s
$ M_b =4 a b d \rho_w $
M_b =4* a * b * d * rho_w
$ M_s =8 a b c \rho_s $
M_s =8* a * b * c * rho_s
$ \displaystyle\frac{ \rho_s }{ \rho_w }= \displaystyle\frac{ d }{ 2 c }$
rho_s / rho_w = d /(2* c )
$ V_b = 4 a b d $
V_b = 4 * a * b * d
$ z_B =-\displaystyle\frac{ d }{2}$
z_B =- d /2
$ z_G = c - d $
z_G = c - d
$ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$
z_M =- d /2 + b ^2/(3* d )
$ z_M \geq z_G $
z_M >= z_G
ID:(15483, 0)
Auftriebs, abhängig von der Masse
Gleichung
Wenn die Auftriebskraft ($F_b$)8661 und die Schwerkraft ($F_g$)4977 gleich sind, wird der Gegenstand schwimmen. In diesem Fall bedeutet das, dass die Masse eines schwimmenden Objekts ($M_s$)8664 gleich die Masse der verdrängte Flüssigkeit ($M_b$)8663 sein muss, was zu folgendem Ergebnis führt:
| $ M_b = M_s $ |
Die Auftriebskraft ($F_b$)8661 wird durch die Flüssigkeitsdichte ($\rho_w$)5407, der Verdrängtes Volumen ($V_b$)8662 und die Gravitationsbeschleunigung ($g$)5310 bestimmt als:
| $ F_b = \rho_w V_b g $ |
was die Schwerkraft ($F_g$)4977 mit die Masse eines schwimmenden Objekts ($M_s$)8664 entgegenwirkt gemäß:
| $ F_g = m_g g $ |
daher, mit die Masse der verdrängte Flüssigkeit ($M_b$)8663 und die Masse eines schwimmenden Objekts ($M_s$)8664,
$F_b = \rho_w V_w g = M_w g = M_s g = F_g$
ergibt sich:
| $ M_b = M_s $ |
Hinweis: Diese Beziehung ist nur möglich, wenn der Gegenstand 'weniger als Wasser wiegt', was bedeutet, dass das verdrängte Wasser ein gleiches oder größeres Volumen als der Gegenstand einnimmt.
ID:(11955, 0)
Objektmasse
Gleichung
Die Masse eines schwimmenden Objekts ($M_s$)8664 kann aus die Objektdichte ($\rho_s$)8665 und dem Volumen, das durch seine geometrischen Parameter der Mittlere Länge des Parallelepipeds ($a$)8673, der Halbe Breite des Parallelepipeds ($b$)8674 und die Halbe Höhe des Parallelepipeds ($c$)8672 gegeben ist, berechnet werden.
Daher gilt:
| $ M_s =8 a b c \rho_s $ |
ID:(11970, 0)
Vom Modellschiff verdrängte Wassermasse
Gleichung
Die Masse der verdrängte Flüssigkeit ($M_b$)8663 kann aus die Flüssigkeitsdichte ($\rho_w$)5407 und dem durch seine geometrischen Parameter der Mittlere Länge des Parallelepipeds ($a$)8673, der Halbe Breite des Parallelepipeds ($b$)8674 und der Tiefgang des Objekts ($d$)8675 gegebenen Volumen berechnet werden.
Daher:
| $ M_b =4 a b d \rho_w $ |
ID:(11971, 0)
Verschobenes Volumen
Gleichung
Der Verdrängtes Volumen ($V_b$)8662 kann aus seinen geometrischen Parametern der Mittlere Länge des Parallelepipeds ($a$)8673, der Halbe Breite des Parallelepipeds ($b$)8674 und der Tiefgang des Objekts ($d$)8675 berechnet werden.
Daher:
| $ V_b = 4 a b d $ |
ID:(11968, 0)
Archimedes 'Prinzip für das Parallelepiped
Gleichung
Das Archimedes-Prinzip besagt, dass die Masse des verdrängten Wassers gleich der Masse des Objekts ist. Für den spezifischen Fall des rechtwinkligen Parallelipeds kann dies wie folgt ausgedrückt werden: die Objektdichte ($\rho_s$)8665, die Flüssigkeitsdichte ($\rho_w$)5407, der Tiefgang des Objekts ($d$)8675 und die Halbe Höhe des Parallelepipeds ($c$)8672:
| $ \displaystyle\frac{ \rho_s }{ \rho_w }= \displaystyle\frac{ d }{ 2 c }$ |
Da das Archimedes-Prinzip besagt, dass die Masse der verdrängte Flüssigkeit ($M_b$)8663 gleich die Masse eines schwimmenden Objekts ($M_s$)8664 ist,
| $ M_b = M_s $ |
ergibt sich, dass die Masse der verdrängte Flüssigkeit ($M_b$)8663 in Beziehung zu die Flüssigkeitsdichte ($\rho_w$)5407, der Mittlere Länge des Parallelepipeds ($a$)8673, der Halbe Breite des Parallelepipeds ($b$)8674 und der Tiefgang des Objekts ($d$)8675 steht wie folgt:
| $ M_b =4 a b d \rho_w $ |
und die Masse eines schwimmenden Objekts ($M_s$)8664 in Beziehung zu die Objektdichte ($\rho_s$)8665, der Mittlere Länge des Parallelepipeds ($a$)8673, der Halbe Breite des Parallelepipeds ($b$)8674 und die Halbe Höhe des Parallelepipeds ($c$)8672 steht wie folgt:
| $ M_s =8 a b c \rho_s $ |
was bedeutet, dass
| $ \displaystyle\frac{ \rho_s }{ \rho_w }= \displaystyle\frac{ d }{ 2 c }$ |
ID:(11972, 0)
Position des Schwimmkraftangriffspunkts
Gleichung
Der Angriffspunkt der Auftriebskraft befindet sich im Schwerpunkt des verdrängten Wasservolumens. Solange das Schiff nicht gekrängt ist, befindet sich dieser Punkt im Zentrum des Volumens auf halber Höhe des Tiefgangs.
Unter Berücksichtigung dessen können Sie die Auftrieb Angriffspunkt ($z_B$)8669 als Funktion von der Tiefgang des Objekts ($d$)8675 ausdrücken:
| $ z_B =-\displaystyle\frac{ d }{2}$ |
ID:(11965, 0)
Position des Angriffspunkts der Gravitationskraft
Gleichung
Der Angriffspunkt der Gravitationskraft entspricht dem Zentrum des Parallelepipedums, das den Rumpf modelliert. Wenn wir das Koordinatensystem auf der Wasseroberfläche festlegen, wird die Höhe des Schwerpunkts ($z_G$)8670 durch Subtraktion von der Tiefgang des Objekts ($d$)8675 von die Halbe Höhe des Parallelepipeds ($c$)8672 erhalten:
| $ z_G = c - d $ |
ID:(11966, 0)
Position des Metazentrums für das Parallelepiped
Gleichung
Die Berechnung von die Höhe des Metazentrums ($z_M$)8671 aus dem Abstand zwischen dem Metazentrum und dem Schwerpunkt des verdrängten Wassers, ausgedrückt durch der Halbe Breite des Parallelepipeds ($b$)8674 und der Tiefgang des Objekts ($d$)8675, erfolgt wie folgt:
| $ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$ |
ID:(11973, 0)
Stabilitätsbedingung
Gleichung
Damit das Objekt stabil ist, muss die Höhe des Metazentrums ($z_M$)8671 immer größer oder gleich die Höhe des Schwerpunkts ($z_G$)8670 sein.
Daher muss es sein:
| $ z_M \geq z_G $ |
ID:(11974, 0)
Stabilitätsbedingung für das Parallelepiped
Gleichung
Für einen rechteckigen Parallelepiped ist die Stabilitätszustand eines Schwimmkörpers ($e$)9835 mit der Halbe Breite des Parallelepipeds ($b$)8674, die Halbe Höhe des Parallelepipeds ($c$)8672 und der Tiefgang des Objekts ($d$)8675:
| $ e = \displaystyle\frac{1}{6}\displaystyle\frac{ b ^2}{ c ^2} - \displaystyle\frac{ d }{2 c }\left(1-\displaystyle\frac{ d }{2 c }\right)$ |
Um sicherzustellen, dass der Quader stabil ist, muss die Höhe des Metazentrums ($z_M$)8671 immer größer oder gleich die Höhe des Schwerpunkts ($z_G$)8670 sein, das heißt
| $ z_M \geq z_G $ |
Daher ist mit die Höhe des Schwerpunkts ($z_G$)8670 als dem Angriffspunkt der gegebenen Auftriebskraft mit die Halbe Höhe des Parallelepipeds ($c$)8672 und der Tiefgang des Objekts ($d$)8675:
| $ z_G = c - d $ |
und die Höhe des Metazentrums ($z_M$)8671 mit der Halbe Breite des Parallelepipeds ($b$)8674:
| $ z_M = -\displaystyle\frac{ d }{2} + \displaystyle\frac{ b ^2}{ 3 d }$ |
erhalten wir die Stabilitätszustand eines Schwimmkörpers ($e$)9835:
| $ e = \displaystyle\frac{1}{6}\displaystyle\frac{ b ^2}{ c ^2} - \displaystyle\frac{ d }{2 c }\left(1-\displaystyle\frac{ d }{2 c }\right)$ |
was größer als eins im Falle einer stabilen Situation und negativ im Falle von Instabilität ist.
ID:(11975, 0)