User:
Buoyancy
Storyboard 
When an object is submerged in a liquid medium, it experiences the pressure of that medium. Because pressure increases with depth, it is greater on the lower part of the object than on the upper part, creating a force upward toward the surface, known as buoyant force. If this force exceeds the object's gravity, it will rise to the surface and float. If it is less, it will slow down the rate of sinking but will continue to descend until it reaches the bottom.
ID:(1609, 0)
Mechanisms
Iframe
Mechanisms
ID:(15480, 0)
Lift
Concept
When an object hanging from a dynamometer is submerged in a liquid, it is observed that the force indicated by it decreases, indicating the existence of a buoyant force a buoyancy force ($F_b$) generated by the liquid.
When an object floats, the buoyant force the buoyancy force ($F_b$) must be equal to the gravitational Force ($F_g$), explaining why it neither sinks nor emerges.
ID:(11951, 0)
Pressure around a submerged body
Concept
To explain the lift experienced by a submerged body, it is necessary to study the vertical pressures to which it is exposed. Since the bottom face of the body is at a greater depth than the top face, the pressure at the bottom is greater than at the top, resulting in a net upward force that generates the observed lift. This phenomenon is similar when a body floats on the surface, where there is no water pressure on it; again, it is the pressure at the bottom that generates lift.
Therefore, in the case where the body is submerged, we obtain:
$\Delta p = p_2 - p_1 = \rho_w g h_2-\rho_w g h_1=\rho_w g (h_2 - h_1) = \rho_w g d$
Or similarly on the surface:
| $ \Delta p = \rho_w g d $ |
Finally, the lift force is obtained using the definition of pressure, which for the pressure at the base ($\Delta p$) with the buoyancy force ($F_b$) and the floating body section ($S_s$) corresponds to:
| $ \Delta p \equiv\displaystyle\frac{ F_b }{ S_s }$ |
ID:(11952, 0)
Archimedes' principle
Concept
A body floats if the buoyant force the buoyancy force ($F_b$) equals the weight of the body the gravitational Force ($F_g$):
| $ F_b = F_g $ |
This implies that the relationship between the mass of floating object ($M_s$) and the mass of the displaced liquid ($M_b$) establishes:
| $ M_b = M_s $ |
Which corresponds to the principle of Archimedes [1].
which states:
Any floating object displaces its own weight in liquid.
[1] "Peri ton eightumenon" (On floating bodies), Archimedes, 287 to 212 BC.
ID:(11956, 0)
Air volume below float level
Concept
Given that with the mass of floating object ($M_s$) and the mass of the displaced liquid ($M_b$),
| $ M_b = M_s $ |
relates to the object Density ($\rho_s$) and the object volume ($V_s$) by
while it holds true that with the liquid density ($\rho_w$) and the ballast volume ($V_w$) we have
| $ M_b = \rho_w ( V_s + V_w )$ |
we obtain the relationship
| $ \rho_s V_s = \rho_w ( V_s + V_w )$ |
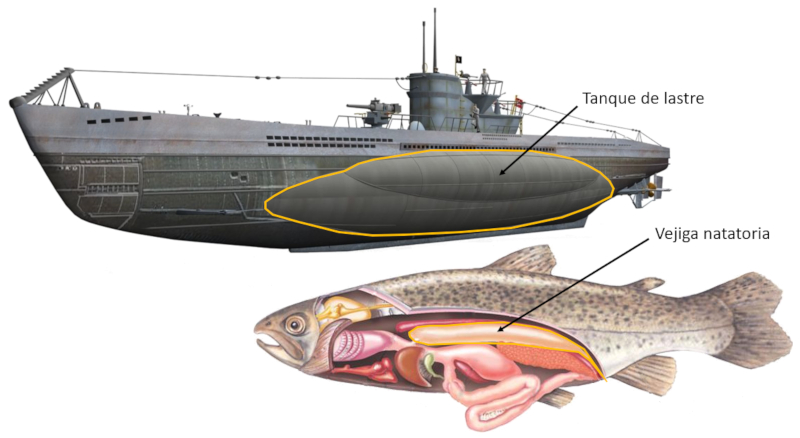
Therefore, an object with a higher density than water can float as long as it has a low volume of air below the waterline (surface of the water). In the case of a boat, this is the space occupied by cargo and/or passengers, while in a submarine, it is the ballast tanks, and in a fish, it is the swim bladder.
It is important to note that:
For a submerged object, suspension, ascent, or descent does not depend on the depth at which it is located. However, the ability to pump air into the ballast tank or swim bladder does depend on the surrounding pressure.
The density of water is not homogeneous in the sea, which means that a submerged object has to adjust the volume of air used in the ballast tank or swim bladder as it moves.
ID:(15706, 0)
Floatation methods
Concept
Submarines and fish have the ability to adjust the depth at which they remain in the water. They can ascend to the surface (float) or descend, limited only by the pressure they can withstand. They achieve this by using ballast tanks (in submarines) and swim bladders (in fish), which are spaces where air can expand, occupying a greater volume of displaced water.
To achieve this, the equality between the mass of the displaced liquid ($M_b$) and the mass of floating object ($M_s$) can be rewritten in terms of the liquid density ($\rho_w$), the object Density ($\rho_s$), and the object volume ($V_s$), allowing for the adjustment of the ballast volume ($V_w$):
| $ \rho_s V_s = \rho_w ( V_s + V_w )$ |
allowing one to be equal to or exceed the other. In summary, if the ballast volume ($V_w$) is increased, buoyancy increases, causing ascent; reducing the volume results in descent. If the volume remains the same, they remain suspended.
An interesting study on how whales use the Spermaceti organ to control buoyancy through heat and fats can be read in the study Buoyancy Control as a Function of the Spermaceti Organ in the Sperm Whale by Malcolm R. Clarke, published in J.mar.bio.Ass U.K. (1978) 58, 27-71.
ID:(11958, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ \Delta p = \rho_w g d $
Dp = rho_w * g * d
$ F_b = F_g $
F_b = F_g
$ F_b = \rho_w V_b g $
F_b = rho_w * V_b * g
$ F_g = M_s g $
F_g = m_g * g
$ M_b = M_s $
M_b = M_s
$ M_b = \rho_w ( V_s + V_w )$
M_b = rho_w *( V_s + V_w )
$ \Delta p \equiv\displaystyle\frac{ F_b }{ S_s }$
p = F / S
$ \rho_w \equiv\displaystyle\frac{ M_b }{ V_b }$
rho = M / V
$ \rho_s \equiv\displaystyle\frac{ M_s }{ V_s }$
rho = M / V
$ \rho_s V_s = \rho_w ( V_s + V_w )$
rho_s * V_s = rho_w *( V_s + V_w )
$ V_b = S_s d $
V = S * h
$ V_b = V_s + V_w $
V_b = V_s + V_w
ID:(15482, 0)
Volume
Equation
The volume ($V$) out of ($$) that does not vary along the height ($h$) is equal to
| $ V_b = S_s d $ |
| $ V = S h $ |
The expression holds even if the shape, but not the value, of section the section ($S$) varies along the height, as long as its total area remains constant.
ID:(3792, 0)
Definition of pressure
Equation
The water column pressure ($p$) is calculated from the column force ($F$) and the column Section ($S$) as follows:
| $ \Delta p \equiv\displaystyle\frac{ F_b }{ S_s }$ |
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
ID:(4342, 0)
Pressure at the base
Equation
The the pressure at the base ($\Delta p$) that exists in the deepest plane of the body is with the object draft ($d$), the liquid density ($\rho_w$), and the gravitational Acceleration ($g$) then:
| $ \Delta p = \rho_w g d $ |
ID:(15484, 0)
Lifting force, depending on the volume
Equation
The buoyancy force ($F_b$) can be expressed in terms of the displaced volume ($V_b$), the liquid density ($\rho_w$), and the gravitational Acceleration ($g$) with:
| $ F_b = \rho_w V_b g $ |
Pressure is defined as:
| $ \Delta p \equiv\displaystyle\frac{ F_b }{ S_s }$ |
The pressure difference is:
| $ \Delta p = \rho_w g \Delta h $ |
The section multiplied by the height of the body is equal to its volume:
| $ V_b = S_s d $ |
Therefore, the buoyant force on a submerged body is:
$F_b = S \Delta p = \rho S \Delta h g = \rho V_s g$
That is:
| $ F_b = \rho_w V_b g $ |
Note: The volume considered here is the submerged volume. If the body is not fully submerged, only the volume corresponding to the displaced liquid should be considered.
ID:(11953, 0)
Gravitational Force
Equation
The gravitational Force ($F_g$) is based on the gravitational mass ($m_g$) of the object and on a constant reflecting the intensity of gravity at the planet's surface. The latter is identified by the gravitational Acceleration ($g$), which is equal to $9.8 m/s^2$.
Consequently, it is concluded that:
| $ F_g = M_s g $ |
| $ F_g = m_g g $ |
ID:(3241, 0)
Buoyancy
Equation
If the gravitational Force ($F_g$) is equal to the buoyancy force ($F_b$):
| $ F_b = F_g $ |
The buoyancy force ($F_b$) is determined by the liquid density ($\rho_w$), the displaced volume ($V_b$), and the gravitational Acceleration ($g$) as:
| $ F_b = \rho_w V_b g $ |
which opposes the gravitational Force ($F_g$) with the mass of floating object ($M_s$) as:
| $ F_g = M_s g $ |
If both forces are equal:
| $ F_b = F_g $ |
the object will float.
the object will float.
ID:(13406, 0)
Buoyancy, as a function of mass
Equation
If the buoyancy force ($F_b$) and the gravitational Force ($F_g$) are equal, the object will float. In this case, it means that the mass of floating object ($M_s$) must be equal to the mass of the displaced liquid ($M_b$), resulting in:
| $ M_b = M_s $ |
The buoyancy force ($F_b$) is determined by the liquid density ($\rho_w$), the displaced volume ($V_b$), and the gravitational Acceleration ($g$) as:
| $ F_b = \rho_w V_b g $ |
which opposes the gravitational Force ($F_g$) with the mass of floating object ($M_s$) according to:
| $ F_g = M_s g $ |
therefore, with the mass of the displaced liquid ($M_b$) and the mass of floating object ($M_s$),
$F_b = \rho_w V_w g = M_w g = M_s g = F_g$
it follows that
| $ M_b = M_s $ |
Note: this relationship is only possible if the object 'weighs less than water', which means the displaced water occupies an equal or greater volume than the object.
ID:(11955, 0)
Mass and Density (1)
Equation
The density ($\rho$) is defined as the ratio between the mass ($M$) and the volume ($V$), expressed as:
| $ \rho_w \equiv\displaystyle\frac{ M_b }{ V_b }$ |
| $ \rho \equiv\displaystyle\frac{ M }{ V }$ |
This property is specific to the material in question.
ID:(3704, 1)
Mass and Density (2)
Equation
The density ($\rho$) is defined as the ratio between the mass ($M$) and the volume ($V$), expressed as:
| $ \rho_s \equiv\displaystyle\frac{ M_s }{ V_s }$ |
| $ \rho \equiv\displaystyle\frac{ M }{ V }$ |
This property is specific to the material in question.
ID:(3704, 2)
Volume with ballast air
Equation
When a body is submerged, the ballast volume ($V_w$) in ballast tank is included with the object volume ($V_s$) in the displaced volume ($V_b$) total. Therefore, we have:
| $ V_b = V_s + V_w $ |
ID:(12015, 0)
Displaced water mass
Equation
With the volume of displaced water equal to the sum of the ballast volume ($V_w$) and the submerged volume ($V_s$), which can be calculated with the liquid density ($\rho_w$), the mass of the displaced liquid ($M_b$) can be determined:
| $ M_b = \rho_w ( V_s + V_w )$ |
Since the displaced volume ($V_b$) is the submerged volume ($V_s$), but including the ballast volume ($V_w$), we have
| $ V_b = V_s + V_w $ |
and the equation for the liquid density ($\rho_w$) represented by
we can calculate the mass of the displaced liquid ($M_b$) as
| $ M_b = \rho_w ( V_s + V_w )$ |
ID:(12016, 0)
Air volume below float level
Equation
The float condition is with the ballast volume ($V_w$), the liquid density ($\rho_w$), the object Density ($\rho_s$) and the object volume ($V_s$):
| $ \rho_s V_s = \rho_w ( V_s + V_w )$ |
Given that with the mass of floating object ($M_s$) and the mass of the displaced liquid ($M_b$),
| $ M_b = M_s $ |
relates to the object Density ($\rho_s$) and the object volume ($V_s$) by
while it holds true that with the liquid density ($\rho_w$) and the ballast volume ($V_w$) we have
| $ M_b = \rho_w ( V_s + V_w )$ |
we obtain the relationship
| $ \rho_s V_s = \rho_w ( V_s + V_w )$ |
ID:(11978, 0)