Circulación superficial en los océanos
Imagen 
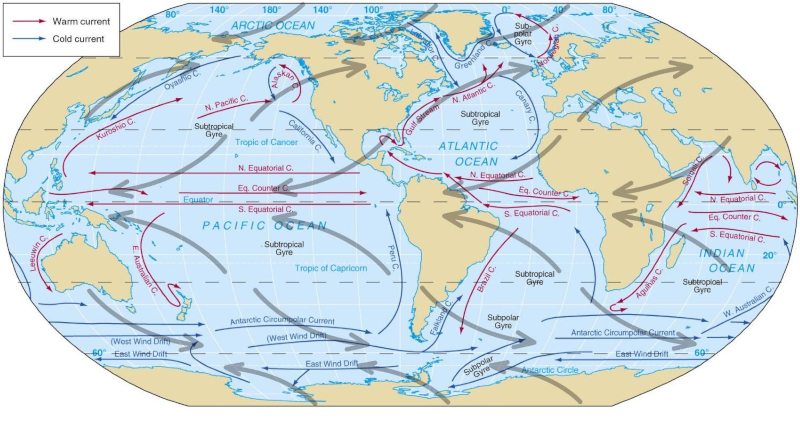
La circulación inducida por los vientos en la atmósfera genera cinco vórtices mayores: dos en el pacifico, dos en el atlántico y uno en el mar indico.
Como anticipado por la ley de Coriolis estos giran en el hemisferio norte en el sentido negativo (como las manecillas del reloj) y positivo en el hemisferio sur (contra las manecillas del reloj).
Se clasifican de frío y caliente según la temperatura que van adquiriendo en las zonas ecuatoriales y polares.
ID:(11676, 0)
Circulación por la formación del domo
Imagen 
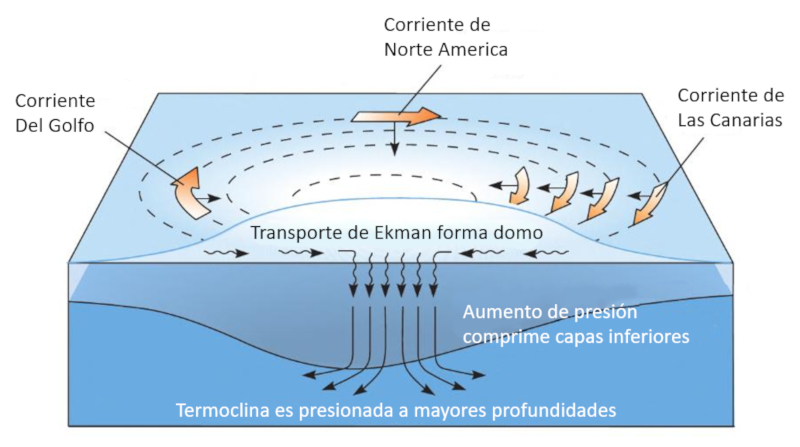
La formación del domo por el flujo hacia el centro del vórtice, que forma un transporte de Ekman, lleva a que la presión con
| p_t = p_0 + \rho_w g h |
generen flujos hacia la profundidad que arrastra agua mas cálida a las profundidades desplazando la termoclina (temperatura).
ID:(11685, 0)
Inclinación del plano isobárico
Descripción 
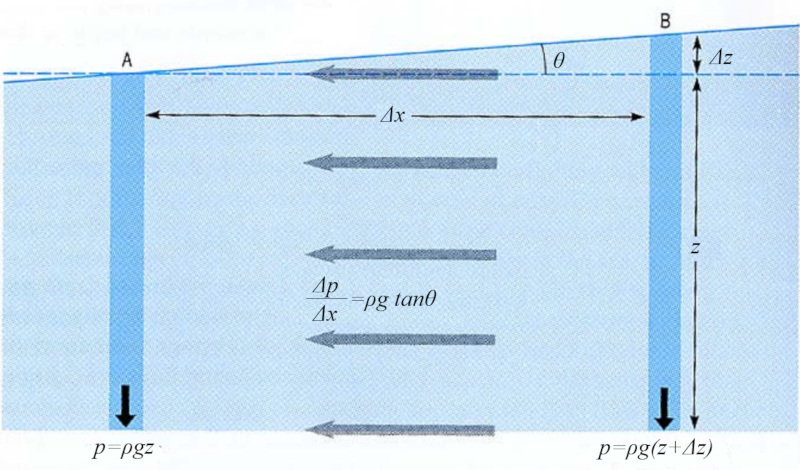
Si la profundidad varía con la posición horizontal, se genera una diferencia de presión que contribuye al desplazamiento del agua.
ID:(12100, 0)
Generación de diferencia de profundidades
Descripción 
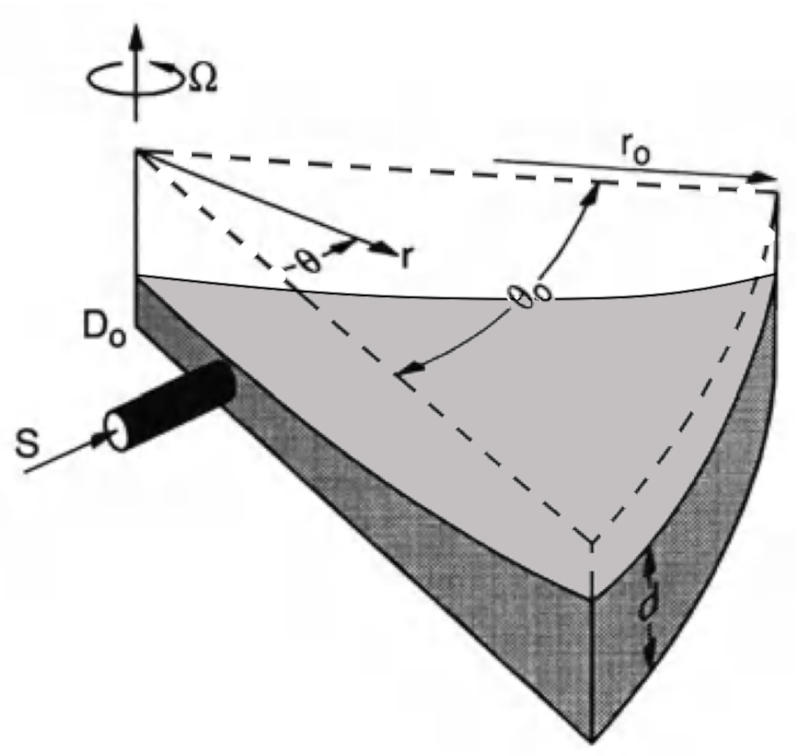
El experimento de Stommel, Arons y Faller demostró cómo una fuente y la fuerza de Coriolis generaron desequilibrios y diferencias de presión para desplazar el agua sin la intervención del viento.
En este caso, tenemos un sistema que rota, por lo tanto, experimenta una aceleración centrífuga, y una fuente de líquido que altera la cantidad en un punto cercano al origen:
ID:(12101, 0)
Profundidad en zonas en circulación
Ecuación 
Al inyectar fluido en la posición de la fuente, se genera un nivel
| d = D_0 + \displaystyle\frac{r^2\omega^2}{2g} |
ID:(12102, 0)
Presión radial por circulación
Ecuación 
Dado que la presión hidrostática depende de la profundidad, podemos expresarla con como:
| p_t = p_0 + \rho_w g h |
La presión en un sistema que rota se puede calcular utilizando y se obtiene:
ID:(12103, 0)
