Oberflächenzirkulation in den Ozeanen
Bild 
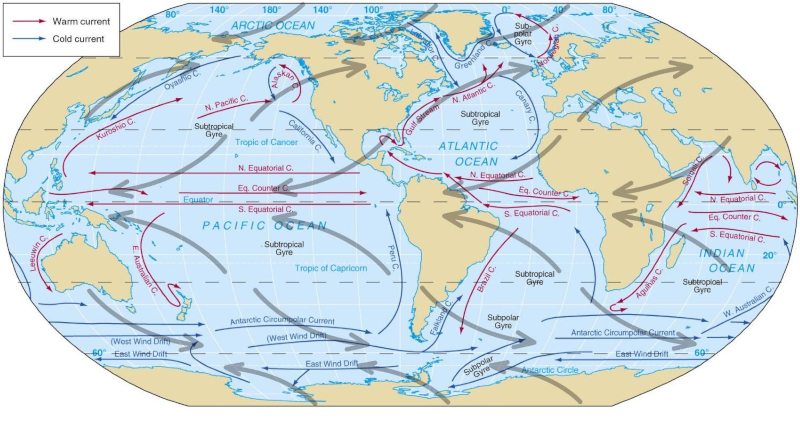
Windinduzierte Zirkulation in der Atmosphäre erzeugt fünf Hauptwirbel: zwei im Pazifik, zwei im Atlantik und einen im Indischen Meer.
Wie vom Coriolis-Gesetz erwartet, drehen sich diese in der nördlichen Hemisphäre in negativer Richtung (wie im Uhrzeigersinn) und positiv in der südlichen Hemisphäre (gegen den Uhrzeigersinn). ).
Sie werden entsprechend der Temperatur, die sie in den äquatorialen und polaren Zonen erfassen, als kalt und heiß klassifiziert.
ID:(11676, 0)
Zirkulation durch Kuppelbildung
Bild 
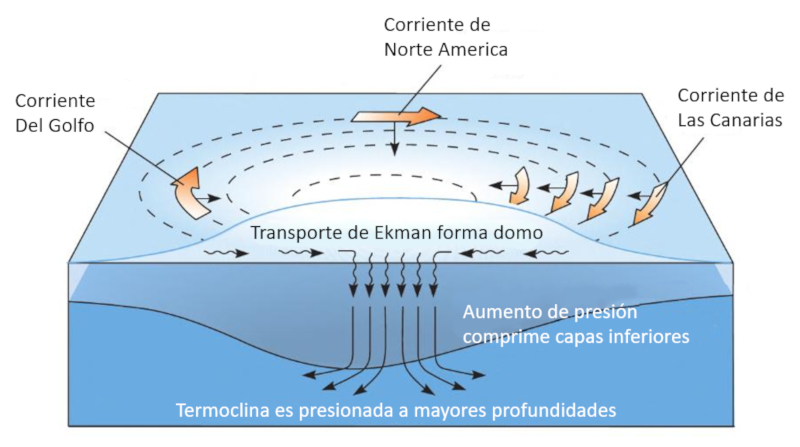
La formación del domo por el flujo hacia el centro del vórtice, que forma un transporte de Ekman, lleva a que la presión con
| p_t = p_0 + \rho_w g h |
generen flujos hacia la profundidad que arrastra agua mas cálida a las profundidades desplazando la termoclina (temperatura).
ID:(11685, 0)
Neigung der isobaren Ebene
Beschreibung 
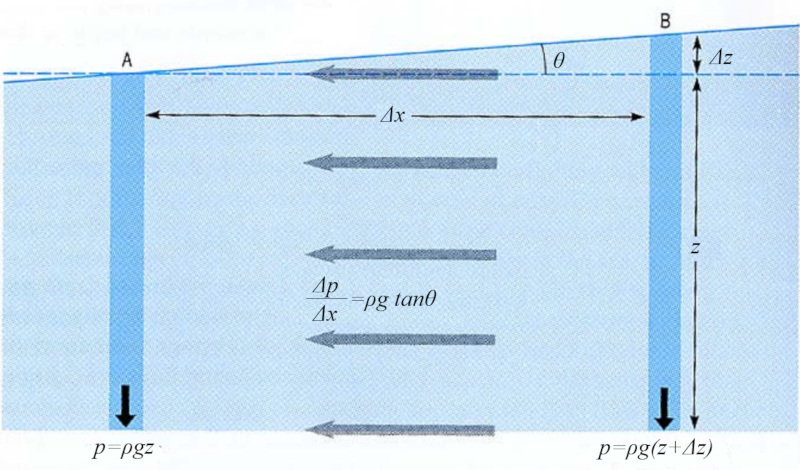
Wenn die Tiefe mit der horizontalen Position variiert, entsteht ein Druckunterschied, der zur Verdrängung des Wassers beiträgt.
ID:(12100, 0)
Erzeugung von Tiefenunterschieden
Beschreibung 
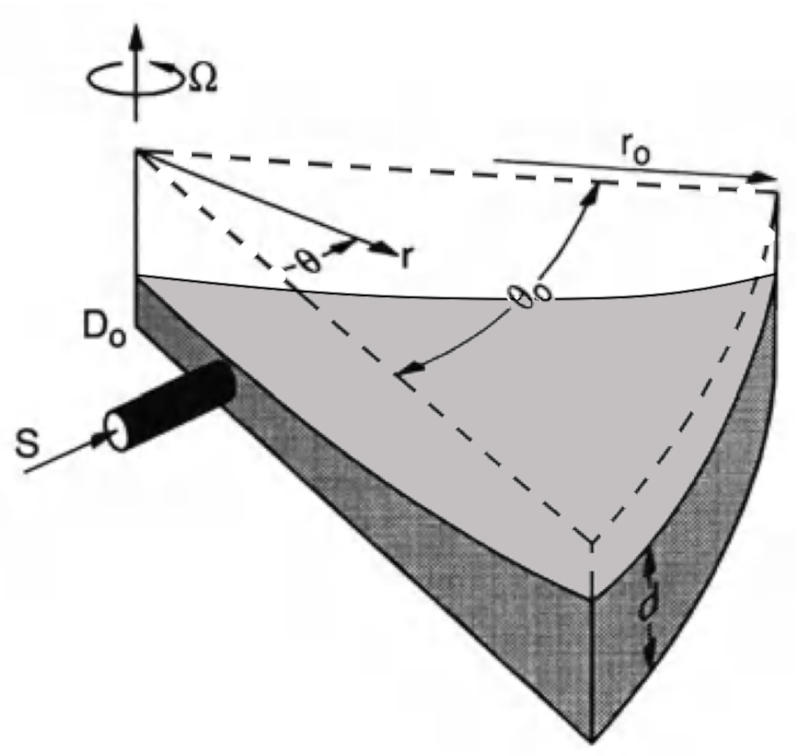
Das Experiment von Stommel, Arons und Faller zeigte, wie eine Quelle und die Corioliskraft Ungleichgewichte und Druckunterschiede erzeugten, um Wasser ohne die Beteiligung des Windes zu verschieben.
In diesem Fall haben wir ein rotierendes System, das eine Zentrifugalbeschleunigung erfährt, und eine Flüssigkeitsquelle, die die Menge an einem Punkt in der Nähe des Ursprungs verändert:
ID:(12101, 0)
Tiefe in Bereichen mit Zirkulation
Gleichung 
Durch das Einspritzen von Flüssigkeit an der Quellposition entsteht ein Pegelstand
| d = D_0 + \displaystyle\frac{r^2\omega^2}{2g} |
ID:(12102, 0)
Radialdruck durch Zirkulation
Gleichung 
Da der hydrostatische Druck von der Tiefe abhängt, können wir ihn mit wie folgt ausdrücken:
| p_t = p_0 + \rho_w g h |
Der Druck in einem rotierenden System kann mit berechnet werden und ergibt sich zu:
ID:(12103, 0)
