Surface circulation in the oceans
Image 
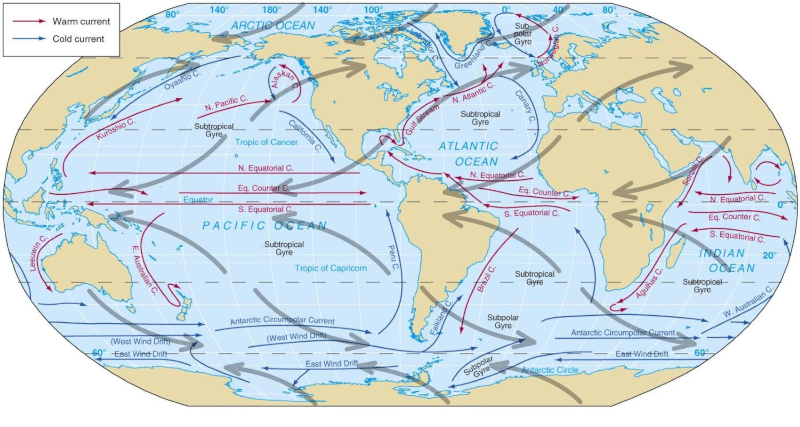
Wind-induced circulation in the atmosphere generates five major vortices: two in the Pacific, two in the Atlantic, and one in the Indian Ocean.
As anticipated by Coriolis law these rotate in the northern hemisphere in the negative direction (clockwise) and positive in the southern hemisphere (counterclockwise) ).
They are classified as cold and hot according to the temperature they are acquiring in the equatorial and polar zones.
ID:(11676, 0)
Circulation by dome formation
Image 
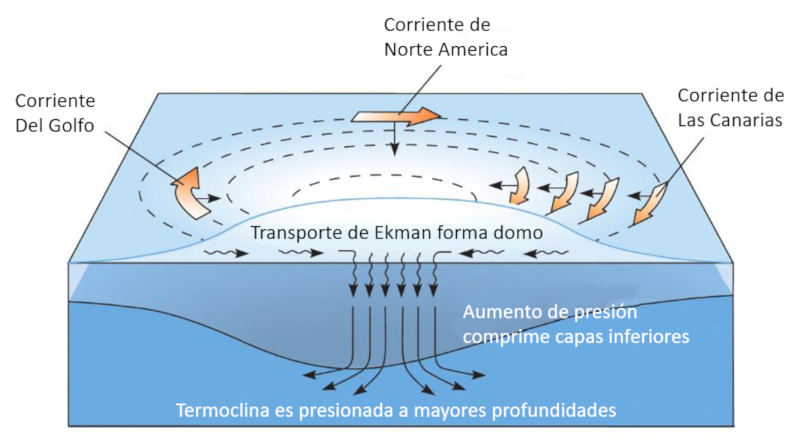
La formación del domo por el flujo hacia el centro del vórtice, que forma un transporte de Ekman, lleva a que la presión con
| $ p_t = p_0 + \rho_w g h $ |
generen flujos hacia la profundidad que arrastra agua mas cálida a las profundidades desplazando la termoclina (temperatura).
ID:(11685, 0)
Isobaric plane inclination
Description 
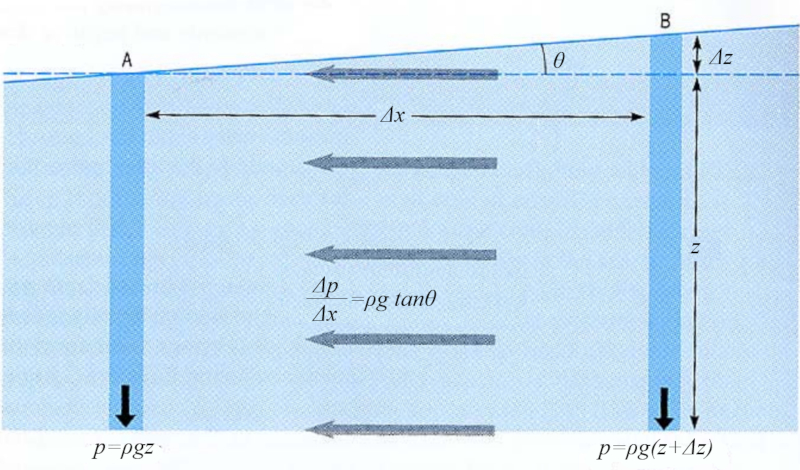
If the depth varies with horizontal position, it creates a pressure difference that contributes to the displacement of water.
ID:(12100, 0)
Depth Difference Generation
Description 
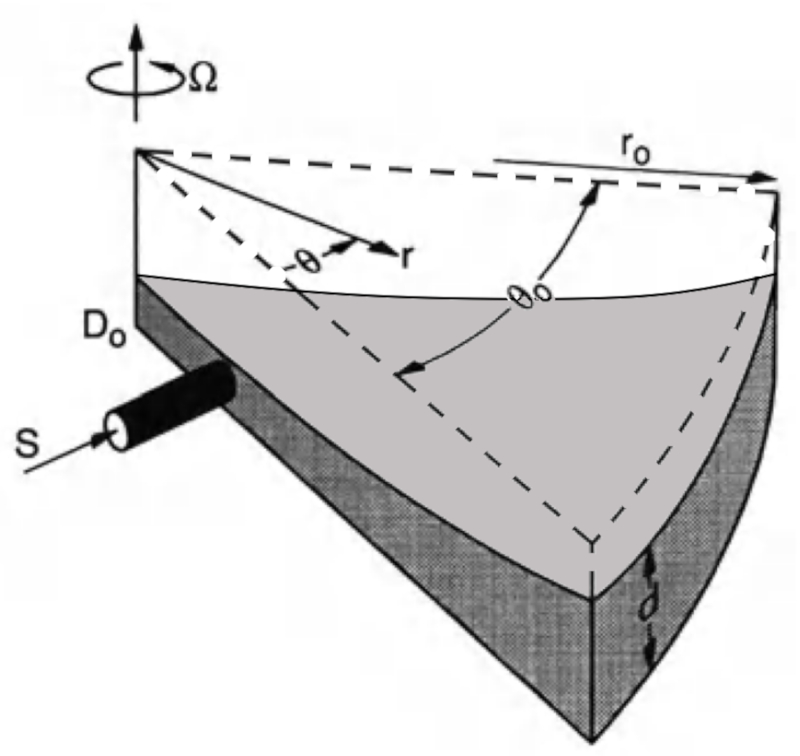
The experiment conducted by Stommel, Arons, and Faller demonstrated how a source and the Coriolis force created imbalances and pressure differences to displace water without the involvement of wind.
In this case, we have a rotating system, experiencing centrifugal acceleration, and a liquid source that alters the quantity at a point near the origin:
ID:(12101, 0)
Depth in circulation areas
Equation 
Injecting fluid at the source position creates a level
| $ d = D_0 + \displaystyle\frac{r^2\omega^2}{2g}$ |
ID:(12102, 0)
Radial pressure by circulation
Equation 
Since hydrostatic pressure is dependent on depth, we can express it with as:
| $ p_t = p_0 + \rho_w g h $ |
The pressure in a rotating system can be calculated using and is given by:
ID:(12103, 0)
