Stability conditions
Storyboard 
There are different structures that are formed by the effect of the Coriolis force and that can be characterized by parameters that, if overcome, form.
ID:(1582, 0)
Stability: Laminar and turbulence
Video 
A fluid that becomes unstable starts forming vortices and eventually exhibits turbulent behavior. Instability can be characterized by the Reynolds number. The video demonstrates the behavior of a liquid based on the Reynolds number:
ID:(11755, 0)
Stability: Reynold number
Equation 
In the case of the Reynolds number, it considers how a liquid or gas forms vortices or turbulence. To do this, it compares inertia with viscous force. If the former is represented by the kinetic energy expressed with velocity
\rho S R U^2
and the latter is represented by the energy associated with viscous force:
\eta S U
where
| Re = \displaystyle\frac{ \rho R U }{ \eta } |
ID:(11756, 0)
Effects scale
Description 
The oscillating systems are grouped into two scales:
- Phenomena associated with circulation are characterized by length and time scales around a velocity of 1 m/s. This includes phenomena such as turbulence (from meters to kilometers and time periods from seconds to hours) to meteorological phenomena (hundreds of kilometers and days to a month).
- Global oscillations can vary in time scale (months, years) but have a global spatial scale (regions or the entire planet).
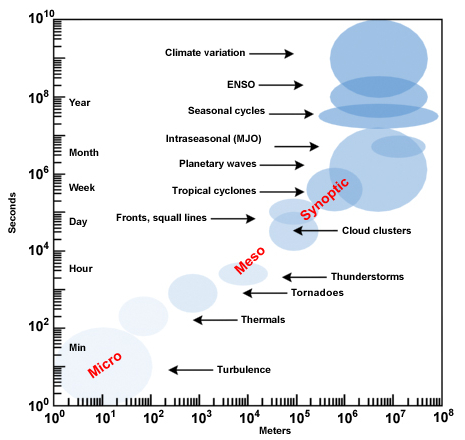
ID:(11752, 0)
Horizontal stability: Rossby number
Equation 
To compare the strength of the Coriolis force with the inertial force, we can define their relationship as a dimensionless characteristic number known as the Rossby number. Since both forces depend on mass and velocity U, the resulting number simplifies to:
The energy associated with the Coriolis force can be estimated by considering the Coriolis force and a characteristic length L. The Coriolis force is the product of mass m, the Coriolis factor f, and velocity U. On the other hand, the energy associated with the inertial force is simply the kinetic energy proportional to mU^2.
Based on this, the Rossby number is defined as:
R_0 = \displaystyle\frac{m U^2}{ m f U L}
Thus, the Rossby number represents the ratio between the fluid's kinetic energy and the effect of the Coriolis force.
| R_0 =\displaystyle\frac{ U }{ f R } |
which depends on the Coriolis factor f and a characteristic length L.
By examining this relationship, we can see that the Rossby number represents the ratio between the characteristic velocity of the fluid and the effect of the Coriolis force. This number indicates whether the system is dominated by inertia or the Coriolis force.
ID:(11753, 0)
