Estabilidade: Laminar e turbulência
Video 
Um fluido que se torna instável começa a formar vórtices e eventualmente exibe um comportamento turbulento. A instabilidade pode ser caracterizada pelo chamado número de Reynolds. No vídeo, é mostrado o comportamento de um líquido em função do número de Reynolds:
ID:(11755, 0)
Estabilidade: número de Reynolds
Equação 
No caso do número de Reynolds, considera-se como um líquido ou gás forma vórtices ou turbulências. Para isso, compara-se a inércia com a força viscosa. Se a primeira é representada pela energia cinética expressa pela velocidade
\rho S R U^2
e a segunda é representada pela energia associada à força viscosa:
\eta S U
onde
| Re = \displaystyle\frac{ \rho R U }{ \eta } |
ID:(11756, 0)
Escala de efeitos
Descrição 
Os sistemas que oscilam estão agrupados em duas escalas:
- Fenômenos associados à circulação estão relacionados a escalas de comprimento e tempo em torno de uma velocidade de 1 m/s. Isso abrange desde fenômenos como turbulência (de metros a quilômetros e períodos de segundos a horas) até fenômenos meteorológicos (centenas de quilômetros e dias a um mês).
- Oscilações globais podem variar em escala temporal (meses, anos), mas possuem uma escala espacial global (regiões ou o planeta como um todo).
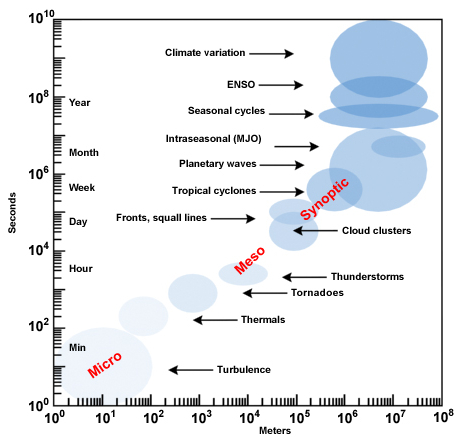
ID:(11752, 0)
Estabilidade horizontal: número de Rossby
Equação 
Para comparar a força de Coriolis com a força inercial, podemos definir sua relação como um número adimensional característico conhecido como número de Rossby. Uma vez que ambas as forças dependem da massa e da velocidade U, o número resultante simplifica-se para:
A energia associada à força de Coriolis pode ser estimada considerando a força de Coriolis e um comprimento característico L. A força de Coriolis é o produto da massa m, o fator de Coriolis f e a velocidade U. Por outro lado, a energia associada à força inercial é simplesmente a en1ergia cinética proporcional a mU^2.
Com base nisso, o número de Rossby é definido como:
R_0 = \displaystyle\frac{m U^2}{ m f U L}
Assim, o número de Rossby representa a relação entre a energia cinética do fluido e o efeito da força de Coriolis.
| R_0 =\displaystyle\frac{ U }{ f R } |
que depende do fator de Coriolis f e de um comprimento característico L.
Ao examinar essa relação, podemos ver que o número de Rossby representa a proporção entre a velocidade característica do fluido e o efeito da força de Coriolis. Esse número nos indica se o sistema é dominado pela inércia ou pela força de Coriolis.
ID:(11753, 0)
