Stabilité: Laminaire et turbulence
Video 
Un fluide qui devient instable commence à former des tourbillons et finit par présenter un comportement turbulent. L\'instabilité peut être caractérisée par le nombre de Reynolds. Dans la vidéo, on montre le comportement d\'un liquide en fonction du nombre de Reynolds :
ID:(11755, 0)
Stabilité: nombre de Reynold
Équation 
Dans le cas du nombre de Reynolds, on considère comment un liquide ou un gaz forme des tourbillons ou des turbulences. Pour ce faire, on compare l\'inertie avec la force visqueuse. Si la première est représentée par l\'énergie cinétique exprimée avec la vitesse
\rho S R U^2
et la seconde est représentée par l\'énergie associée à la force visqueuse :
\eta S U
où
| Re = \displaystyle\frac{ \rho R U }{ \eta } |
ID:(11756, 0)
Échelle des effets
Description 
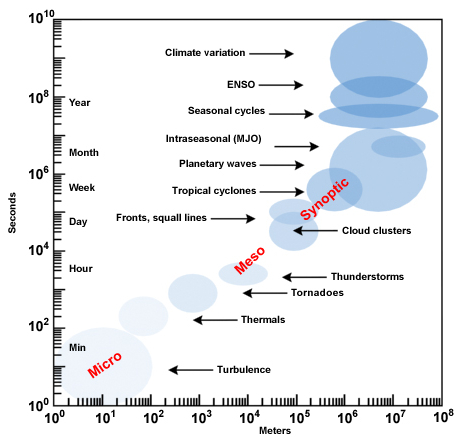
Les systèmes oscillants sont regroupés en deux échelles :
- Les phénomènes associés à la circulation se caractérisent par des échelles de longueur et de temps autour d\'une vitesse de 1 m/s. Cela inclut des phénomènes tels que la turbulence (de quelques mètres à quelques kilomètres et des périodes de quelques secondes à quelques heures) ainsi que les phénomènes météorologiques (des centaines de kilomètres et des durées de quelques jours à un mois).
- Les oscillations globales peuvent varier en termes d\'échelle temporelle (mois, années), mais elles ont une échelle spatiale globale (régions ou la planète entière).
ID:(11752, 0)
Stabilité horizontale: nombre de Rossby
Équation 
Pour comparer la force de Coriolis à la force inertielle, nous pouvons définir leur relation comme un nombre adimensionnel caractéristique connu sous le nom de nombre de Rossby. Étant donné que ces deux forces dépendent de la masse et de la vitesse U, le nombre résultant se simplifie à :
L'énergie associée à la force de Coriolis peut être estimée en considérant la force de Coriolis et une longueur caractéristique L. La force de Coriolis est le produit de la masse m, du facteur de Coriolis f et de la vitesse U. D\'autre part, l\'énergie associée à la force inertielle est simplement l\'énergie cinétique proportionnelle à mU^2.
Sur cette base, le nombre de Rossby est défini comme suit :
R_0 = \displaystyle\frac{m U^2}{ m f U L}
Ainsi, le nombre de Rossby représente le rapport entre l\'énergie cinétique du fluide et l\'effet de la force de Coriolis.
| R_0 =\displaystyle\frac{ U }{ f R } |
qui dépend du facteur de Coriolis f et d'une longueur caractéristique L.
En examinant cette relation, nous pouvons constater que le nombre de Rossby représente la proportion entre la vitesse caractéristique du fluide et l\'effet de la force de Coriolis. Ce nombre nous indique si le système est dominé par l\'inertie ou par la force de Coriolis.
ID:(11753, 0)
