Storyboard

The power of the sun that finally reaches a place on the face of the earth depends on the one hand on the distance to the sun, the inclination of the axis and the rotation of the planet.

>Model

ID:(533, 0)

Description

>Top

The Earth's orbit forms an ellipse in which the Sun is located at one of the foci:

The plane containing the orbit is called the ecliptic.

The point farthest from the Sun is called the aphelion (July 7th), and the closest point is called the perihelion (January 3rd). The midpoints where the Earth passes through the point where the radius coincides with the semi-minor axis are known as solstices.

The radii are referred to as the major axis (a) and the minor axis (b).

The parameters of the orbit are as follows:

Parameters | Variable | Value

|:---------------|:----------|:-----------:

Major axis (Semi-major axis) | $a$ | $149,598,000 km$

Minor axis (Semi-minor axis) | $b$ | $149,577,000 km$

Aphelion | | $152.1 \times 10^6 km$

Perihelion | | $147.1 \times 10^6 km$

Orbital eccentricity | $\epsilon$ | $0.0167$

Period | $T$ | $365.256 days$

Average velocity | | $29,780 m/s$

ID:(3079, 0)

Description

>Top

An ellipse can be drawn by fixing a string to two points (the foci) and extending the string to its maximum length, then drawing points around both foci with a pencil:

None

ID:(3081, 0)

Description

>Top

The position of the Earth is described in terms of the coordinates $(x, y)$, with the center of the ellipse taken as the origin:

ID:(3080, 0)

Equation

>Top, >Model

The $x$ coordinate of the Earth's position as a function of time $t$ is expressed as:

$x=a\,\cos\left(\displaystyle\frac{2\pi t}{T}\right)$

Conditions

Variables

$T$

Period of the Orbit

$s$

6487

$\pi$

Pi

3.1415927

$rad$

5057

$x_t$

Position along the Semi Major Axis

$m$

6488

$a$

Semi Major Axis of the Earth's Orbit

$m$

6485

$t$

Time in Years

$s$

6491

Relation

ID:(4658, 0)

Equation

>Top, >Model

The $y$ coordinate of the Earth's position as a function of time $t$ is expressed as:

$y=a\,\sin\left(\displaystyle\frac{2\pi t}{T}\right)$

Conditions

Variables

$T$

Period of the Orbit

$s$

6487

$\pi$

Pi

3.1415927

$rad$

5057

$y_t$

Position along the Semi Minor Axis

$m$

6489

$b$

Semi Minor Axis of the Earth's Orbit

$m$

6486

$t$

Time in Years

$s$

6491

Relation

ID:(4659, 0)

Equation

>Top, >Model

The distance between the Sun and the Earth, denoted as $r$, can be calculated from the square of the coordinates:



where the coordinates are:

using the formula:

thus obtaining:

$r=\sqrt{a^2\sin^2\left(\displaystyle\frac{2\pi t}{T}\right)+b^2\cos^2\left(\displaystyle\frac{2\pi t}{T}\right)}$

Conditions

Variables

$r$

Distance earth sun

$m$

6490

$T$

Period of the Orbit

$s$

6487

$\pi$

Pi

3.1415927

$rad$

5057

$a$

Semi Major Axis of the Earth's Orbit

$m$

6485

$b$

Semi Minor Axis of the Earth's Orbit

$m$

6486

$t$

Time in Years

$s$

6491

Relation

In this case, $a$ represents the major axis, $b$ the minor axis, and $T$ the period of the orbit.

For comparison, the average distances from the Sun to the planets are listed below:

Planet | Average Orbit Radius [km] | Orbital Period [years]

|:-----------|:---------------------------------------------:|:---------------------:

Mercury | 5.7909227E+7 | 0.2408467

Venus | 1.08209475E+8 | 0.61519726

Earth | 1.49598262E+8 | 1.0000174

Mars | 2.27943824E+8 | 1.8808476

Jupiter | 7.78340821E+8 | 11.862615

Saturn | 1.426666422E+9 | 29.447498

Uranus | 2.870658186E+9 | 84.016846

Neptune | 4.498396441E+9 | 164.79132

Source: NASA/Lunar and Planetary Institute

ID:(4660, 0)

Description

>Top

Since the orbit is an ellipse, it has a degree of deformation that is measured by its eccentricity.

The values for different planets are listed below:

Planet | Eccentricity [-]

|:-----------|:------------------:|

Mercury | 0.20563593

Venus | 0.00677672

Earth | 0.01671123

Mars | 0.0933941

Jupiter | 0.04838624

Saturn | 0.05386179

Uranus | 0.04725744

Neptune | 0.00859048

Source: NASA/Lunar and Planetary Institute

Therefore, almost all planets have an orbit that is approximately circular.

ID:(3088, 0)

Description

>Top

The axis of the Earth has an inclination of 23.5 degrees with respect to the ecliptic.

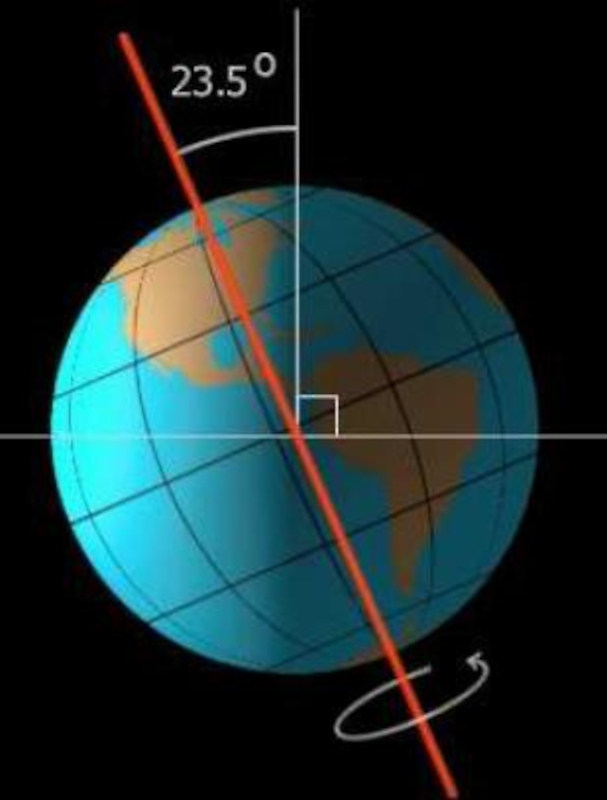
The inclination of the axis is the reason why the radiation received by each hemisphere of the planet varies between the moments when the planet is at perihelion and aphelion.

The values for the inclination of different planets are listed below:

Planet | Inclination [degrees]

|:--------|:--------------------------:|

Mercury | 0

Venus | 177.3

Earth | 23.4393

Mars | 25.2

Jupiter | 3.1

Saturn | 26.7

Uranus | 97.8

Neptune | 28.3

Note: Values greater than 90 degrees correspond to "retrograde rotations," which means rotations in the opposite direction.

Source: NASA/Lunar and Planetary Institute

ID:(3085, 0)

Html

>Top

Debido a la inclinación del eje terrestre la intensidad de luz solar varia durante el año dependiendo de la posición de la tierra en torno al sol.

ID:(6869, 0)