Storyboard

The fluctuations of the Earth's orbit have a direct effect on the radiation balance and with it the Earth's climate.

>Model

ID:(538, 0)

Description

>Top

As a first approximation, Mars can be considered to have no atmosphere, allowing for a relatively simple modeling approach:

ID:(3070, 0)

Description

>Top

In the case of an atmosphere-less planet, there is a fraction of the incident radiation $I_p$ that is reflected as $a_{
u}I_p$, another fraction is absorbed as $(1-a_{
u})I_p$, and a fraction of the infrared radiation $\sigma\epsilon T_e^4$ is emitted:

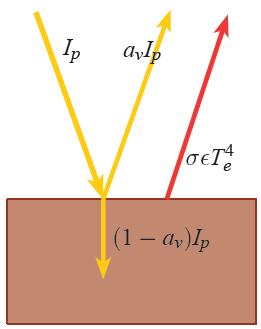
ID:(3069, 0)

Equation

>Top, >Model

The planet absorbs and re-emits radiation received from the sun. The absorbed energy by the planet corresponds to the radiation not reflected, which can be expressed as

$(1-a_v)I_s$

This energy heats up the planet to a temperature $T_p$. The resulting heating leads to infrared radiation, which can be described by the Stefan-Boltzmann law as

$\sigma\epsilon T_p^4$

where $\sigma$ is the Stefan-Boltzmann constant and $\epsilon$ is the emissivity.

In an equilibrium state, the absorbed energy and the emitted energy are equal, given by

$(1-a_v)I_s=\sigma\epsilon T_p^4$

This equation allows us to calculate the temperature $T_p$ of the planet:

$ T_p =\left(\displaystyle\frac{(1- a_v ) I_s }{ \sigma \epsilon }\right)^{1/4}$

Conditions

Variables

$a_{VIS}$

Albedo Visible (VIS)

$-$

7722

$I_s$

Average earth intensity

$W/m^2$

6502

$\epsilon$

Emissivity

$-$

5242

$T_p$

Planet Temperature

$K$

6505

$\sigma$

Stefan Boltzmann constant

1.38e-23

$J/m^2K^4s$

5241

Relation

Using this equation to estimate the temperatures of different planets, we obtain the following data:

Planet | Intensity [W/m^2] | Albedo [-] | Temperature [C] | Range [C]

:----------|:---------------------------|:-------------|:----------------------|:--------------:

Mercury | 9126.49 | 0.088 | 345.83 | -180 to 430

Venus | 2613.78 | 0.76 | 51.17 | 465

Earth | 1367.56 | 0.306 | 86.54 | -89 to 58

Mars | 589.04 | 0.25 | 23.95 | -82 to 0

Jupiter | 50.52 | 0.503 | -128.09 | -150

Saturn | 15.04 | 0.342 | -158.22 | -170

Uranus | 3.71 | 0.3 | -190.86 | -200

Neptune | 1.51 | 0.29 | -207.18 | -210

It is interesting to note the deviations, especially for planets closer to the sun, which are influenced by their respective atmospheres.

In this model, surface variations and atmospheric altitude changes are not taken into account. Therefore, the planet is modeled as a zero-dimensional point (0D).

ID:(4669, 0)

Description

>Top

Apart from nutation, the Earth's axis undergoes a rotational movement known as precession.

None

The consequence of precession is that the timing of summer and winter changes over time. With a precession period of 26,000 years, every 13,000 years the seasons are reversed.

ID:(3087, 0)

Equation

>Top, >Model

Si la intensidad visible del sol es I_s y el albedo de la superficie a_v, la intensidad reflejada será con

ID:(4668, 0)

Description

>Top

The solar intensity fluctuates depending on the precision of the orbit:

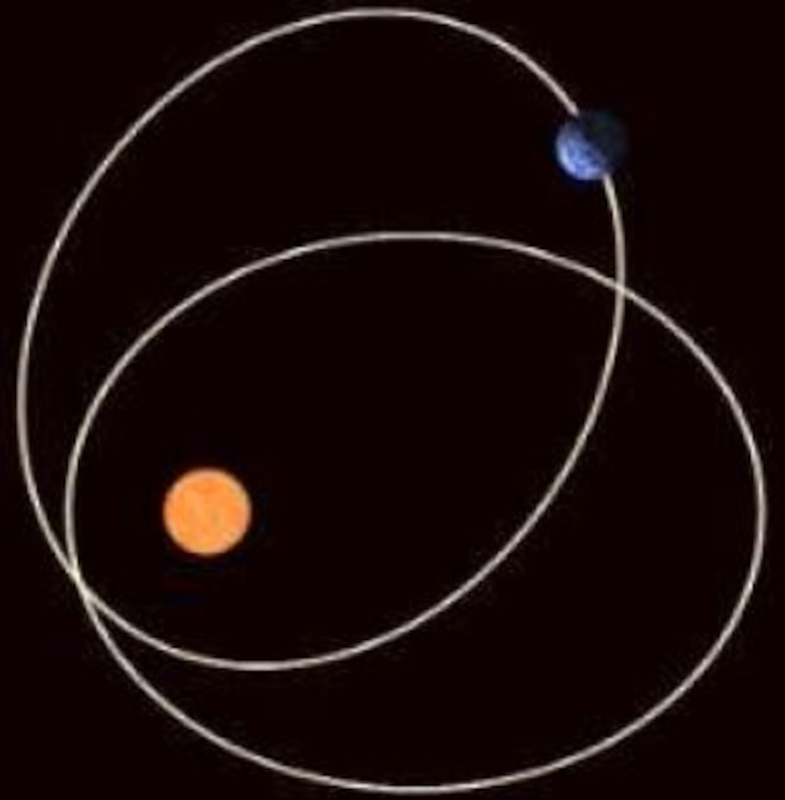
None

ID:(3089, 0)

Description

>Top

The Earth's axis varies in its inclination between 22.1 and 24.5 degrees. This process is called nutation.

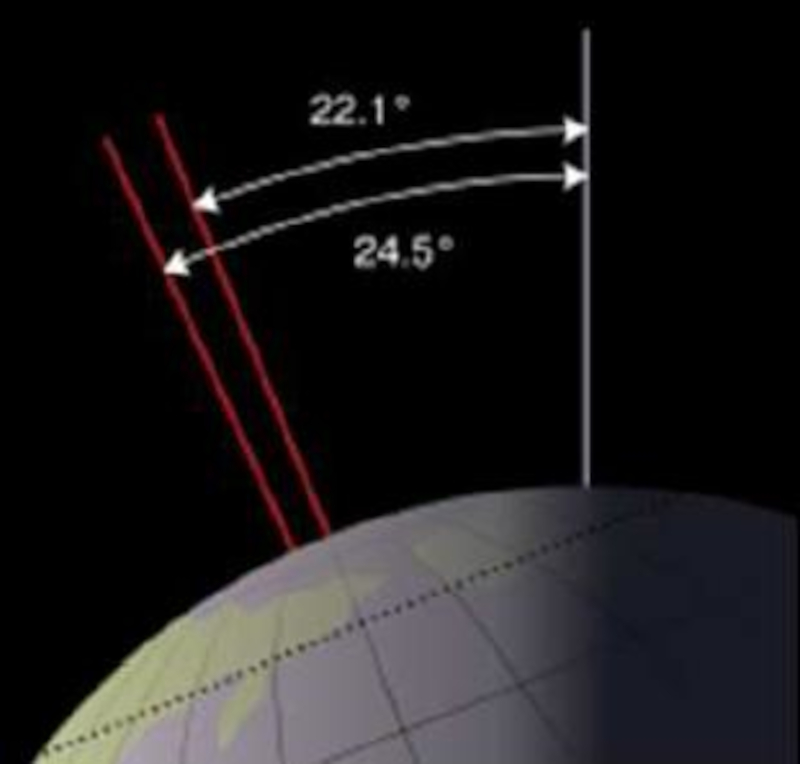
Nutation is caused by factors such as the gravitational influence of the Moon on Earth and the Earth's non-perfectly spherical shape. Each factor has its own typical period, with the longest being around 41,000 years. It is believed that the last maximum value occurred approximately 10,700 years ago (8,700 BC), coinciding with the end of the last Ice Age.

ID:(3086, 0)

Description

>Top

Fluctuations in the orientation of the axis and variations in the Earth's orbit have led to a decrease in solar radiation reaching the planet, resulting in periods of cooling and the formation of ice ages.

None

The last ice age ended approximately 10,000 years ago.

ID:(3090, 0)